
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение линейных скоростей точек механизма и угловых скоростей звеньев механизмаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Точка А кривошипа ОА совершает вращательное движение, поэтому вектор скорости u
Для определения скорости точки
В этой системе уравнений известны по модулю и направлению векторы скоростей точек А и С (скорость точки А была определена выше, а скорость точки С равна 0). Векторы относительных скоростей неизвестны по величине, но известны по направлению: вектор Для построения выбираем на плоскости произвольную точку Рu – полюс плана скоростей, которая является началом отсчёта, и откладываем на ней отрезок Этот отрезок изображает на плане скоростей вектор скорости
В соответствии с первым уравнением системы (1.5) на плане скоростей через точку а проводим прямую, перпендикулярную к звену 2 механизма (линия вектора Для определения действительной величины скорости любой точки достаточно умножить длину соответствующего вектора на масштабный коэффициент
Чтобы определить скорость точки D, воспользуемся теоремой подобия. Величину отрезка
Действительная величина скорости точки D равна:
2.7. Определение ускорений точек звеньев механизма Определение ускорений точек звеньев механизма выполняется в той же последовательности, что и определение скоростей. Первой точкой, ускорение которой надо определить, является точка А входного звена 1. При вращательном движении кривошипа ОА ускорение
Так как звено 1 вращается с постоянной угловой скоростью (w1 = const), то
Следовательно, в этом частном случае полное ускорение
и направлено параллельно звену ОА от точки А к точке О (центру вращения). Рассматривая точку В, как принадлежащую одновременно звеньям 2 и 3, ускорение точки В может быть представлено в виде суммы двух векторов:
Относительные ускорения
Величины нормальных составляющих относительных ускорений
Вектор нормальной составляющей Тангенциальные составляющие ускорений Таким образом, выражения (1.13,б) представляют систему двух векторных уравнений с четырьмя неизвестными, которая может быть решена графическим методом с помощью построения плана ускорений. Для этого выбираем на плоскости произвольную точку Ра – полюс плана ускорений, которая является началом отсчёта, и откладываем от неё отрезок
В соответствии с первым уравнением системы (1.13,б) через точку а, плана ускорений проводим прямую, параллельную звену АВ в направлении от точки В к точке А, и на ней откладываем отрезок
величина которого в масштабе изображает вектор нормальной составляющей ускорения Через точку n2 перпендикулярно к звену АВ (или тоже самое, что перпендикулярно отрезку В соответствии со вторым уравнением системы (1.13,б) из полюса Ра (точка С совпадает с полюсом) проводим прямую, параллельную звену ВС, в направлении от точки В к точке С и откладываем отрезок
Через точку n3 перпендикулярно звену ВС проводим линию вектора тангенциальной составляющей ускорения Точка b пересечения двух прямых, изображающих линии действия тангенциальных составляющих ускорений, представляет графическое решение системы (1.13, б). Соединяя точку b с полюсом плана ускорения Pa, получим отрезок
а В =
Вектор
Значения тангенциальных составляющих относительных ускорений вычисляем по формулам:
Для определения ускорения точки D воспользуемся теоремой подобия. Величина отрезка
Численная величина абсолютного ускорения точки D механизма равна
аD =
Ускорения asi центров масс звеньев определяются аналогично с помощью теоремы подобия. Например, в соответствии с исходными данными центр массы S3 звена 3 делит отрезок CD пополам. На плане ускорений точка s 3 также будет делить отрезок cd пополам. Ускорение центра масс а s3, м∙с-2
а s3 =
Аналогично а s 2 =
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 904; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.236.144 (0.007 с.) |

 , м/с, точки А направлен перпендикулярно звену 1 в сторону вращения и численно равен по модулю
, м/с, точки А направлен перпендикулярно звену 1 в сторону вращения и численно равен по модулю , (1.4)
, (1.4)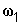 – угловая скорость звена ОА, с-1;
– угловая скорость звена ОА, с-1;  – длина звена ОА, м.
– длина звена ОА, м. В составляют векторные уравнения, связывающие искомую скорость точки с известными скоростями точек А и С. Так как точка В принадлежит звену 2, то ее скорость равна векторной сумме абсолютной скорости
В составляют векторные уравнения, связывающие искомую скорость точки с известными скоростями точек А и С. Так как точка В принадлежит звену 2, то ее скорость равна векторной сумме абсолютной скорости  точки А и скорости
точки А и скорости  точки В относительно точки А. В то же время точка В принадлежит звену 3 и ее скорость равна векторной сумме абсолютной скорости
точки В относительно точки А. В то же время точка В принадлежит звену 3 и ее скорость равна векторной сумме абсолютной скорости 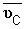 точки С и скорости
точки С и скорости 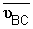
 точки В относительно точки С. Следовательно,
точки В относительно точки С. Следовательно,
 , (1.5)
, (1.5) , перпендикулярный к звену ОА, в направлении движения точки А.
, перпендикулярный к звену ОА, в направлении движения точки А. точки А. Назначив его длину, определяют масштабный коэффициент
точки А. Назначив его длину, определяют масштабный коэффициент  ,
,  , плана скоростей:
, плана скоростей: . (1.6)
. (1.6)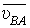 ). В соответствии со вторым уравнением через полюс (точка C совпадает с полюсом) проводим на плане прямую, перпендикулярно к звену 3 механизма (это линия вектора
). В соответствии со вторым уравнением через полюс (точка C совпадает с полюсом) проводим на плане прямую, перпендикулярно к звену 3 механизма (это линия вектора  ). Точка b пересечения этих двух прямых, является концом вектора
). Точка b пересечения этих двух прямых, является концом вектора 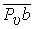 , изображающего на плане вектор скорости
, изображающего на плане вектор скорости  и равного ему вектора
и равного ему вектора  Вектор
Вектор  изображает в масштабе относительную скорость
изображает в масштабе относительную скорость  .
. ×
×  ×
×  ;
;  ; (1.7)
; (1.7) находим из пропорции:
находим из пропорции: =
=  ;
;  . (1.8)
. (1.8)
 =
=  ×
×  точки А можно представить в виде векторной суммы двух составляющих: нормальной и тангенциальной
точки А можно представить в виде векторной суммы двух составляющих: нормальной и тангенциальной . (1.11)
. (1.11) (1.11, а)
(1.11, а) точки А определяется только величиной нормальной составляющей
точки А определяется только величиной нормальной составляющей  , которое по модулю равно:
, которое по модулю равно:
 (1.12)
(1.12) , (1.13,а)
, (1.13,а) и
и 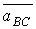 представим в виде суммы двух составляющих: нормальной и тангенциальной. Тогда:
представим в виде суммы двух составляющих: нормальной и тангенциальной. Тогда: , (1.13,б)
, (1.13,б) , (1.14)
, (1.14) направлен вдоль звена АВ от точки В к точке А, а вектор нормальной составляющей
направлен вдоль звена АВ от точки В к точке А, а вектор нормальной составляющей  – вдоль звена ВС от точки В к точке С.
– вдоль звена ВС от точки В к точке С.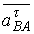 и
и 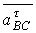 по абсолютной величине неизвестны, но известны по направлению: они направлены перпендикулярно к нормальным составляющим.
по абсолютной величине неизвестны, но известны по направлению: они направлены перпендикулярно к нормальным составляющим. параллельно звену ОА в направлении от точки А к точке О в соответствии со схемой механизма (см. рисунок 3,в). Длина этого отрезка изображает на плане вектор
параллельно звену ОА в направлении от точки А к точке О в соответствии со схемой механизма (см. рисунок 3,в). Длина этого отрезка изображает на плане вектор 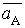 ускорения точки А и выбирается произвольно. Тогда масштабный коэффициент плана ускорений
ускорения точки А и выбирается произвольно. Тогда масштабный коэффициент плана ускорений  ,
, 
 /
/ 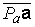 . (1.15)
. (1.15) , мм
, мм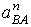 /
/  .
. ) проводим линию вектора тангенциальной составляющей
) проводим линию вектора тангенциальной составляющей  .
. /
/ 
 .
. , изображающий на плане ускорений вектор ускорения точки В механизма. Величину этого ускорения находим с помощью масштабного коэффициента:
, изображающий на плане ускорений вектор ускорения точки В механизма. Величину этого ускорения находим с помощью масштабного коэффициента: , проведённый из точки а в точку b, на плане ускорений соответствует масштабному выражению вектора полного относительного ускорения
, проведённый из точки а в точку b, на плане ускорений соответствует масштабному выражению вектора полного относительного ускорения  , абсолютная величина которого равна:
, абсолютная величина которого равна: =
= 
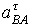 =
=  ×
×  =
=  ×
×  может быть найдена из соотношения:
может быть найдена из соотношения: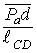 =
=  , т.е.
, т.е.  . (1.21)
. (1.21) ×
×  ×
× 


