
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кручение. Расчет на жесткостьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
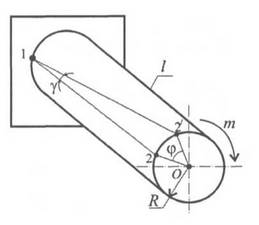
Кручением называется такой вид деформации стержня, при котором в поперечных сечениях возникает только одно внутреннее усилие – крутящий момент Мк. Крутящий момент считается положительным, если при взгляде на оставшуюся часть стержня со стороны отброшенной части момент направлен против хода часовой стрелки. Стержень, испытывающий деформацию кручения, называется валом. Условие жесткости записывается в виде Расчет на жесткость При расчете на жесткость определяется деформация и сравнивается с допускаемой. Рассмотрим деформацию круглого бруса над действием внешней пары сил с моментом т (рис. 27.4).
Произведение GJP называют жесткостью сечения. Модуль упругости можно определить как G Обычно рассчитывается угол закручивания, приходящийся на:дин метр длины бруса (вала) φо. Условие жесткости при кручении можно записать в виде
где φо — относительный угол закручивания, [φо] ≈ 1град/м = 0,02 рад/м - допускаемый относительный гол закручивания.
1.16 1.17 Изгиб Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб. Часто термин «прямой» в названии прямого чистого и прямого поперечного изгиба не употребляют и их называют соответственно чистым изгибом и поперечным изгибом. Опоры балок, рассматриваемых как плоские системы, бывают трех основных типов.
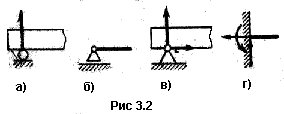
1. Подвижная шарнирная опора (рис. 3.2, а). Такая опора не препятствует вращению конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через центр катка. Схематичное изображение подвижной шарнирной опоры дано на рис. 3.2, б. Подвижные опоры дают возможность балке беспрепятственно изменять свою длину при изменении температуры и тем самым устраняют возможность появления температурных напряжений. 2. Неподвижная шарнирная опора (рис. 3.2, в). Такая опора допускает вращение конца балки, но устраняет поступательное перемещение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие - горизонтальную и вертикальную. 3. Жесткая заделка, или защемление (рис. 3.2, г). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в общем случае возникать реакция, которую обычно раскладывают на две составляющие (вертикальную и горизонтальную) и момент защемления (реактивный момент). Балка с одним заделанным концом называется консольной балкой или просто консолью. Если опорные реакции могут быть найдены из одних уравнений статики, то балки называют статически определимыми. Если же число неизвестных опорных реакций больше, чем число уравнений статики, возможных для данной задачи, то балки называют статически неопределимыми. Для определения реакций в таких балках приходится составлять дополнительные уравнения - уравнения перемещений.
Рассмотрим пример
1. Приравняем нулю сумму проекций на ось Х всех сил, действующих на балку: Sх=0, Ах=0. 2. То же, на ось У: Sу=0 Ау – Р1 – q·а3=0 Ау = Р1 + q·а3 = 20 + 20·2= 60 кН Вертикальная составляющая реакций в консольной балке равна сумме сил, приложенных к балке.
SМА=0 МА + Р1·2 + q· 2 · 5=0 МА = -Р1·2 - q· 10 = -20·2 - 20· 10= -240 кН ·м Знак (-) показывает, что направление момента следует изменить на обратное. Реактивный момент в заделке равен S моментов внешних сил относительно заделки.
При плоском поперечном изгибе в поперечных сечениях возникают два внутренних усилия М изгибающий и поперечная сила Q.
Отбросим одну из частей (правую) и рассмотрим равновесие левой части. Взаимодействие частей балки заменим внутренними усилиями: М изгибающий и поперечная сила Q. Для определения Мизг. и Q используем 2 уравнения равновесия: 1. Sу=0 Ау – Р1 + Q =0; Q = Р1 – Ау; Q = S (Рi) у 2. S М0 =0 Ах – Р1 (х –а1) + М = 0 М = Р1 (х –а1) – Ах; М = S т0 (Рi) Таким образом, поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от сечения. Эпюры поперечных сил, изгибающих моментов. Общий порядок построения. 1. Определяем опорные реакции и делаем проверку. 2. Разбиваем балку на участки. За границы участков нагружения принимаем сечения, где приложены внешние силовые факторы, а также начало и конец распределенной нагрузки. 3. Применяя метод сечений, составим выражения для поперечных сил Q и изгибающих моментов Мизг. 4. По этим выражениям строим эпюры Q и Мизг., соблюдая правила знаков Q и Мизг. 5. На эпюре Q в месте приложения сосредоточенной нагрузки есть скачок равный этой силе, на эпюре Мизг скачок равен моменту, приложенному в данном сечении. I Σ Х = 0 RХА = 0 ΣУ = 0 RАУ + RВУ – 2Р = 0 RАУ + RВУ = 2Р RАУ = RВУ = Р Проверка: Σ МА = 0 RВУ · 4а – Р · 3А – РА = 0 0 = 0
II 3 участка нагружения III Метод сечений: Первое сечение Q = RА = Р Мизг = RАХ1; если Х1 - 0 → Второе сечение Мизг = 0; если Х1 = а → Мизг = Ра Q = RА - Р = Р – Р = 0 Мизг = RА · (а + х2 ) – РХ2 = РХ2 Ра – РХ2 = Ра Третье сечение Q = -RВ = - Р Мизг = RВ X3 = РХ3 Если Х3 = 0 → Мизг = 0 Если Х3 = а → Мизг = Ра
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.24 (0.007 с.) |

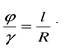 . Здесь φ - угол закручивания; γ – угол сдвига; l - длина бруса; R - радиус; R=d/2. Откуда
. Здесь φ - угол закручивания; γ – угол сдвига; l - длина бруса; R - радиус; R=d/2. Откуда 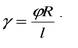 . Закон Гука имеет вид τk = Gγ. Подставим выражение для γ, получим
. Закон Гука имеет вид τk = Gγ. Подставим выражение для γ, получим 
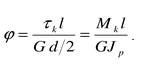 .
. 0,4Е. Для стали G = 0,8·105 МПа.
0,4Е. Для стали G = 0,8·105 МПа.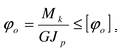 ,
, ;
;
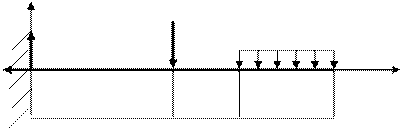
 Для их определения применим метод сечений. Сделаем мысленно разрез балки на расстоянии х от опоры А
Для их определения применим метод сечений. Сделаем мысленно разрез балки на расстоянии х от опоры А




