
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжение в любой точке поперечного сеченияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Элементарный момент силы dQ относительно центра круга dm = pdQ, где р — расстояние от точки до центра круга. Суммарный момент сил упругости получаем сложением (интегрированием) элементарных моментов:
После преобразования получим формулу для определения напряжений в точке поперечного сечения: Эвольвентное зубчатое колесо и его параметры. Толщина зуба колеса по окружности произвольного радиуса. Понятие о исходном, исходном производящем и производящем контурах. Станочное зацепление. Основные размеры зубчатого колеса. Виды зубчатых колес. Подрезание и заострение колеса. Понятие о области существования зубчатого колеса. Эвольвентная цилиндрическая зубчатая передача и ее параметры. Основные уравнения эвольвентного зацепления.
При ρ = 0 τк = 0; касательное напряжение при кручении пропорционально расстоянию от точки до центра сечения. Полученный интеграл Jp называется полярным моментом инерции сечения. Jр является геометрической характеристикой сечения при кручении. Она характеризует сопротивление сечения скручиванию. Анализ полученной формулы для Jр показывает, что слои, расположенные дальше от центра, испытывают большие напряжения. Эпюра распределения касательных напряжений при кручении (рис. 27.3)
Решение первой задачи сводится к определению необходимого числа функций времени (уравнений движения), однозначно определяющих положение каждой точки тела в пространстве. Решение второй задачи заключается в определении зависимостей, позволяющих по известным уравнениям движения определить траекторию, а также скорость и ускорение любой точки тела в любой момент времени. Поля́рный моме́нт ине́рции — интегральная сумма произведений площадей элементарных площадок dA на квадрат расстояния их от полюса — ρ2 (в полярной системе координат), взятая по всей площади сечения. То есть:
Эта величина используется для прогнозирования способности объекта оказывать сопротивление кручению. Она имеет размерность единиц длины в четвёртой степени (м4, cм4) и может быть лишь положительной. Для площади сечения, имеющей форму круга радиусом r полярный момент инерции равен:
Если совместить начало декартовой прямоугольной системы координат 0 с полюсом полярной системы (см. рис.), то
потому что
Полярный момент инерции для некоторых случаев
Распределение касательных напряжений при кручении Для круглого сплошного сечения:
где D — диаметр круга. Для кольцевого сечения (полый вал):
где D — внешний диаметр кольца, d — внутренний диаметр кольца.
Кручение Круче́ние — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил(момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор— крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию. Угол закручивания цилиндрического стержня в границах упругих деформаций под действием момента T может быть определён из уравнения закона Гука для случая кручения
где:
G — модуль сдвига. Отношение угла закручивания φ к длине
Деформация кручения является частным случаем деформации сдвига ГУКА ЗАКОН - основной закон теории упругости, выражающий линейную зависимость между напряжениями и малыми деформациями в упругой среде. Установлен P. Гуком (R. Hooke) в 1660. При растяжении стержня длиной l его удлинение При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи: а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку; б) проектировочный расчет - определить размеры вала из условия его прочности; в) расчет по несущей способности - определить максимально допустимый При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении: · по схеме вала и действующим на него скручивающим моментам строят · выбирают материал для рассчитываемого вала и определяют для этого материала допускаемое напряжение · для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении
Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:
Для сплошного круглого сечения
Определив размеры вала из условия прочности, проверяют вал на жесткость по формуле
где Если данное условие не выполняется, то необходимо выбрать размеры вала из условия жесткости:
Учитывая, что для сплошного круглого сечения
Окончательно выбирают диаметр d, удовлетворяющий условиям прочности и жесткости.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 Рис. 27.2
Рис. 27.2
 .
. , где
, где  .
. — максимальное напряжение.
— максимальное напряжение.
 Рис. 27.3
Рис. 27.3



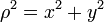 .
.




 — геометрический полярный момент инерции;
— геометрический полярный момент инерции; — длина стержня;
— длина стержня;
 пропорц. растягивающей силе F; в этом случае Г. з. имеет вид
пропорц. растягивающей силе F; в этом случае Г. з. имеет вид  , где
, где  - нормальное напряжение в поперечном сечении стержня,
- нормальное напряжение в поперечном сечении стержня,  - относит. удлинение, S - площадь поперечного сечения. Константа материала E наз. модулем Юнга. При этом относит. изменение поперечных размеров стержня
- относит. удлинение, S - площадь поперечного сечения. Константа материала E наз. модулем Юнга. При этом относит. изменение поперечных размеров стержня  пропорц. относительному удлинению:
пропорц. относительному удлинению: 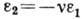 . Константа
. Константа  наз. коэф. Пуассона.
наз. коэф. Пуассона. ;
; (5.15)
(5.15) (5.16)
(5.16) , отсюда можем записать выражение для определения диаметра вала из условия его прочности:
, отсюда можем записать выражение для определения диаметра вала из условия его прочности: (5.17)
(5.17) , (5.18)
, (5.18) - допустимый относительный угол закручивания вала.
- допустимый относительный угол закручивания вала. (5.19)
(5.19) , можем записать выражение для определения диаметра вала из условия его жесткости:
, можем записать выражение для определения диаметра вала из условия его жесткости: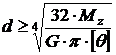 (5.20)
(5.20)


