Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подбор сечения балки из прокатного двутавраСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Строят эпюры Qx и Mx (см. практическую работу № 9). 2. Подбирают сечение стальной балки в следующем порядке: а) определяют требуемый момент сопротивления сечения балки:
где Мmax - наибольший по абсолютному значению изгибающий момент, принимаемый по эпюре Mx; R – расчетное сопротивление материала по пределу текучести (прил. VIII); б) по ГОСТам прил. I подбираем номер двутавровой стальной балки, которая должна иметь момент сопротивления Wx, наиболее близкий к значению требуемого момента сопротивления 3. Проверяют прочность принятой двутавровой балки по нормальным напряжениям. Такую проверку выполняют для сечения с нибольшим изгибающим моментом:
где Wx – момент сопротивления приятого сечения. Если условие удовлетворительно, то прочность балки по нормальным сечениям считается обеспеченной, и наоборот. 4. Строят эпюру нормальных напряжений s. Для этого вычерчивают крупно поперечное сечение балки и проводят на отдельном рисунке нулевую линию перпендикулярно нейтральной оси. Затем на уровне крайних точек сечения (верхней и нижней) откладывают найденные ранее значения smax и smin и соединяют эти значения прямой линией. Полученный график называется эпюрой s. Значения smax и smin откладывают по разные стороны от нулевой линии. 5. Проверяют прочность принятой двутавровой балки по касательным напряжениям. наибольшие касательные напряжения возникают в том сечении по длине балки, в котором действует наибольшая поперечная сила (по абсолютному значению), а по высоте сечения – на уровне нейтральной оси. Для определения этих напряжений действительное сечение двутавра упрощают: полка и стенка принимаются прямоугольными: полка с размерами b и t, а стенка – d (см. прил. I). таким образом, сечение двутавра теперь состоит из трех прямоугольников. Касательные напряжения на уровне нейтральной оси определяют по формуле Журавского:
где Qx – поперечная сила в рассматриваемом сечении балки; Sx – статический момент сечения, расположенного выше или ниже нейтральной оси; Проверяют прочность балки по касательным напряжениям
где RS – расчетное сопротивление материала сдвигу (прил. VIII). 6. Строим эпюру касательных напряжений t. К4асательные напряжения изменяются по высоте балки по криволинейному закону и имеют скачок в месте соединения полки и стенки. Поэтому эпюру t строят по значениям, найденным в пяти точках сечения: крайних точках, на уровне нейтральной оси и на уровне сопряжения стенки и полки — чуть ниже и чуть выше этого сопряжения. Напряжение в этих точках определяется по формуле Журавского. При этом статический момент Sx и ширина сечения b определяются для каждой точки сечения. Касательные напряжения в крайних точках сечения равны нулю.
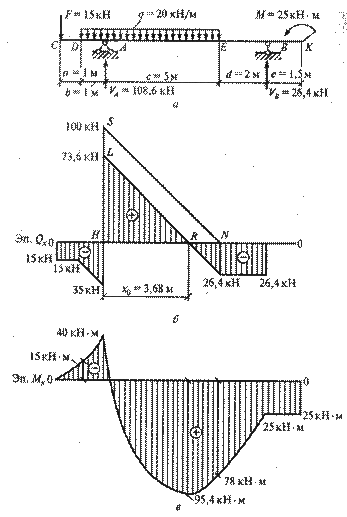
Пример 14. Подобрать сечение стальной двутавровой балки (рис. 46, а). Проверить прочность принятого сечения по нормальным напряжениям в сечении с наибольшим изгибающим моментом и по касательным напряжениям в сечении с наибольшей поперченной силой. Материал – сталь марки С-235. Решение. 1. Строим эпюры Qx и Mx (см. пример 10, практическая работа № 9). Наибольшее значение поперечной силы Qmax =73,6кН, изгибающего момента Mmax=95,4кН∙м (см. рис. 25).
Рис. 25
2. Подберем сечение стальной двутавровой балки по наибольшему изгибающему моменту
где R =230 МПа – расчетное сопротивление стали марки С-235 (прил. VIII). По табл. 3 прил. I принимаем двутавр № 30 с 3. Проверим прочность принятого сечения:
Прочность сечения по нормальным напряжениям обеспечена. 4. Строим эпюру нормальных напряжений. Отложим от нулевой линии 0-0 (рис. 26, б) значение
Рис. 26
5. Проверим прочность балки по касательным напряжениям. заменим действительное сечение упрощенным (рис. 26, в). Размеры приняты по табл. 3 прил. I. Определим наибольшее касательное напряжение
где
Подставим числовые значения в формулу:
Проверим прочность сечения по касательным напряжениям:
т.е. прочность обеспечена. В прокатных балках, которые не несут больших сосредоточенных сил в приопорных участках, это условие обычно соблюдается с большим запасом. 6. Построим эпюру касательных напряжений. Напряжение в сечении 2-2
где Напряжение в сечении 3-3
где b =13,5см, т.к. сечение 3-3 проходит в полке. Напряжение в сечении 4-4 равно нулю, т.к. По найденным значениям строим эпюру ty (рис. 26, г).
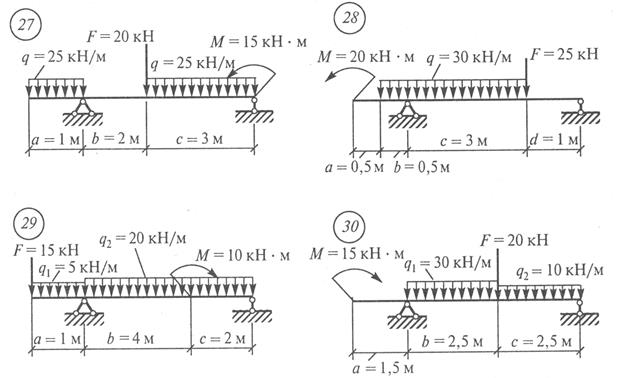
Задание для практической работы № 13. Подобрать сечение стальной двутавровой балки (рис. 27), проверить принятое сечение по нормальным и по касательным напряжениям и построить эпюры s и t для соответствующих сечений. Материал – сталь С-245.
Рис. 27
Рис. 27 Продолжение
Рис. 27 Продолжение
Рис. 27 Окончание
Практическая работа № 14
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 7163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ,
,

 ,
,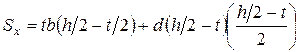 ; Jx – момент инерции всего сечения, принимается по табл. 3 прил. I; b – ширина сечения балки на уровне нейтральной оси.
; Jx – момент инерции всего сечения, принимается по табл. 3 прил. I; b – ширина сечения балки на уровне нейтральной оси. ,
,
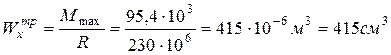 ,
, что больше чем
что больше чем 

 и
и  и соединим полученные точки. Верхняя часть испытывает сжатие, нижняя – растяжение, т.к. по эпюре Mx видно, что балка прогибается (обращена выпуклостью) вниз.
и соединим полученные точки. Верхняя часть испытывает сжатие, нижняя – растяжение, т.к. по эпюре Mx видно, что балка прогибается (обращена выпуклостью) вниз.
 ,
,
 .
. ,
, ,
,
 ,
,