
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка прочности балки при плоском поперечном изгибеСодержание книги
Поиск на нашем сайте
Общие положения Плоским поперечным изгибом называется такое напряженно-деформированное состояние балки, при котором из всех внутренних силовых факторов не равны нулю только поперечная сила в направлении одной оси и изгибающий момент относительно другой главной центральной оси инерции сечения балки. Плоский поперечный изгиб реализуется, когда нагрузка приложена в продольной плоскости симметрии или приводится к ней в каждом поперечном сечении. Если такой плоскости у балки нет, то нагрузка должна быть приложена в одной из главных плоскостей инерции балки (главная плоскость инерции – это плоскость, проходящая через одну через одну из главных центральных осей поперечного сечения и продольную ось балки). Проверка прочности предусматривает определение внутренних силовых факторов Q(z) и М(z) в каждом сечении балки, нахождение по ним максимальных по модулю нормальных - s, касательных - t и эквивалентных - sэкв напряжений в соответствующих точках балки и сравнение названных напряжений с допускаемыми. Методические указания к выполнению проверки прочности балки и пример расчета приведены в подразделах 4.2 и 4.3. Методические указания 1. Начертить в удобном масштабе расчетную схему балки, указать на ней числовые значения сил, нагрузок, моментов, длин пролетов, консолей и участков, показать реакции опор, пронумеровать участки. 2. Составить уравнения равновесия балки, определить опорные реакции и нанести их значения на схему. 3. Применить метод сечений при определении поперечных сил Q и изгибающих моментов М, построить эпюры Q и М. При построении эпюр согласно этому методу следует мысленно разрезать балку на две части в пределах каждого участка произвольно намеченным и зафиксированным по длине поперечным сечением. Причем, фиксированная координата по длине балки для данного поперечного сечения может отсчитываться от общего начала координат слева и справа балки или отдельно в пределах каждого участка. Отбросить одну часть, например, правую. Заменить ее действие на левую искомыми внутренними усилиями Q и М. Найти эти усилия из уравнений равновесия системы сил, приложенных к левой части, включая и сами Q и М. Поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил.
Изгибающий момент М в поперечном сечении балки численно равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения относительно центра тяжести сечения. Поперечная сила в сечении балки считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз, и отрицательной – если направлена в противоположные стороны.
Изгибающий момент считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз, и отрицательным – выпуклостью вверх. Записать аналитические выражения для поперечной силы Q(z) и изгибающего момента М(z) для каждого участка балки и вычислить значения Q(z) и М(z) на границах каждого участка. Если зависимость для изгибающего момента на участке криволинейна, а поперечная сила на границах этого участка имеет разный знак, то следует определить координату z на этом участке, где поперечная сила равна нулю, и для этой точки вычислить экстремальное значение изгибающего момента. По полученным значениям построить графики – эпюры Q(z) и М(z). 4. Используя дифференциальные зависимости при изгибе:
проверить правильность построения обеих эпюр. 5. Подобрать из условия прочности балки по нормальным напряжениям двутавровое сечение по моменту сопротивления Wх:
Выписать из сортамента геометрические характеристики сечения Wx, Jх – осевой момент инерции, Sx – статический момент полусечения, s – толщина стенки, b и t – ширина и толщина полки двутавра. 6. Определить максимальные нормальные напряжения по формуле:
и построить эпюру s в сечении балки. 7. Проверить прочность балки по касательным напряжениям:
и построить эпюру касательных напряжений t в стенке двутавра, рассчитав их в точках перехода к полке по формуле:
8. Проверить прочность балки по III теории прочности:
Так как расчетное напряжение зависит от s и t, то проверке подлежит тот элемент материала балки, для которых s и t будут одновременно возможно большими и это осуществимо при наличии таких двух условий: а) изгибающий момент и поперечная сила достигают наибольшей величины в одном и том же сечении по длине балки;
б) ширина резко меняется вблизи краев сечения (например, в двутавре или пустотелом прямоугольном профиле). Нормальные и касательные напряжения на уровне перехода от полки к стенке (в точках «к» см. рис.8) для таких профилей имеют величину, близкую максимальной. Указанные два условия, таким образом, определяют и необходимость дополнительной проверки прочности, а также сечение и точку на нем, для которых эта проверка должна быть сделана. Если эти условия не имеют места, тогда следует выбрать несколько поперечных сечений по длине балки и несколько точек по высоте сечения, могущих дать наиболее высокие значения расчетного напряжения. Для двутаврового сечения:
Значения М и Q в формулах (7) и (8) берутся для одного выбранного сечения.
Рис. 8 Пример расчета Для двутавровой балки (рис. 9а) Построить эпюры Q и М. Из условия прочности по нормальным напряжениям подобрать двутавровое сечение балки, если [s] = 160 МПа. Построить эпюру s в стенке двутавра. Проверить прочность балки по касательным напряжениям, если [t] = 100 МПа. Построить эпюру t в сечении балки. Проверить прочность балки по III теории прочности. Исходные данные: С = 1 м; а = 2 м; b = 3 м; Определение опорных реакций
Проверка:
Рис. 9
2. Построение эпюры поперечных сил Q
При
При
При Эпюра Q показана на рис. 9б. 3. Построение эпюры М изгибающих моментов
При
Найдем экстремум изгибающего момента:
Отсюда
При При
При z = 0 M3 = 0; При z = 1 M3 = –70 кНм; По полученным значениям ординат на участках построена эпюра М (рис. 9в). 1. Из условия прочности по нормальным напряжениям произведем подбор сечения балки.
Из сортамента выбираем двутавр № 36 с Wх = 743 см3; Jх = 13380 см4; b = 14,5 см; Sх = 423 см3; t = 1,23 см; S = 0,75 см. 2. Определим максимальные нормальные напряжения по формуле:
Эпюра нормальных напряжений в сечении показана на рис. 9г. Поскольку максимальный изгибающий момент отрицательный, то верхние волокна растянуты, а нижние сжаты. 3. Проверим прочность балки по касательным напряжениям. Из рис. 9б видно, что максимальная поперечная сила на опоре В. Поэтому проверку по касательным напряжениям проведем при Qmax = 102 кН.
τmax = 43 МПа <[τ] = 100 МПа. Определим касательные напряжения в точке К – точке перехода от стенке к полке двутавра.
Эпюра касательных напряжений в стенке двутавра приведена на рис. 9г. Проверка прочности балки по третьей теории прочности. С использованием построенных эпюр Q и М определяем, что опасным сечением будет сечение на опоре А, где М = 100 кН×м; Q = 98 кН. В опасном сечении в точке перехода от полки к стенке двутавра определим нормальные и касательные напряжения. σ = τ = σэкв =
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.135.243 (0.007 с.) |



 (4.2.1)
(4.2.1) (4.2.2)
(4.2.2) (4.2.3)
(4.2.3) (4.2.4)
(4.2.4) (4.2.5)
(4.2.5) (4.2.6)
(4.2.6) (4.2.7)
(4.2.7) (4.2.8)
(4.2.8)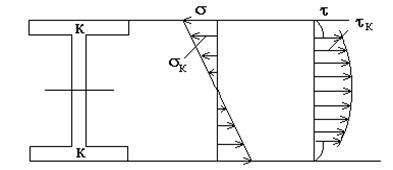
 = 5 м; q1 = 20 кНм; q2 = 40 кНм; М = 100 кНм; Р1 = 40 кН; Р2 = 50 кН; [σ ] = 160 МПа; [ τ ] = 100 МПа.
= 5 м; q1 = 20 кНм; q2 = 40 кНм; М = 100 кНм; Р1 = 40 кН; Р2 = 50 кН; [σ ] = 160 МПа; [ τ ] = 100 МПа.

 кН;
кН;

 кН
кН



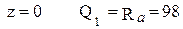 кН; При
кН; При 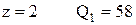 кН;
кН;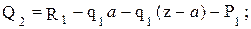
 кН; При
кН; При  кН;
кН;
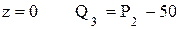 кН; При
кН; При  кН;
кН;
 кНм; При
кНм; При  кНм;
кНм;

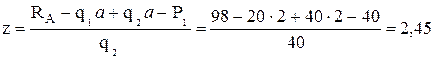 м;
м; кНм; При
кНм; При  кНм;
кНм; кНм;
кНм;
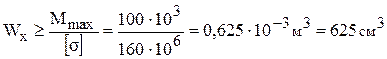

 = 43 МПа <[τ] = 100 МПа.
= 43 МПа <[τ] = 100 МПа.
 32 МПа
32 МПа =
=  = 126 МПа;
= 126 МПа; =
=  = 30 МПа;
= 30 МПа; = 140 МПа.
= 140 МПа.


