
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет статически неопределимой балкиСодержание книги
Поиск на нашем сайте
Общие замечания Балка называется статически неопределимой, если число неизвестных реакций больше числа уравнений статики, которые могут быть применены для их нахождения. Разность между числом неизвестных реакций и числом уравнений равновесия называется степенью статической неопределимости. Как и раньше, при решении статически неопределимых стержневых систем, для составления дополнительных уравнений перемещений следует рассмотреть условия совместности перемещений в такой балке. В сопротивлении материалов часто рассматриваются два способа раскрытия статической неопределимости в балках: теорема о трех моментах и способ приравнивания перемещений. Теорема о трех моментах – это зависимость, связывающая три изгибающих момента, появляющихся на опорах любых двух смежных пролетов неразрезной многопролетной балки, с нагрузкой, действующей на эти два смежных пролета. Так как на крайних опорах изгибающий момент известен, после нахождения изгибающих моментов на промежуточных опорах, многопролетную балку можно представить в виде однопролетных статически определимых балок, загруженных внешней нагрузкой данного пролета и вычисленными изгибающими моментами на опорах. Для шарнирно опертых однопролетных балок с помощью уравнений статики можно найти реакции на всех опорах. Если на крайних опорах изгибающие моменты неизвестны, например, когда балка начинается или заканчивается консолью или защемлением, то моменты могут быть найдены следующим образом. Если у балки имеется консоль, то момент на прилегающей к консоли опоре находится методом сечений. Если имеется защемление, то оно заменяется дополнительным шарнирно опертым пролетом, длина которого равна нулю. Это дает возможность записать дополнительные уравнения трех моментов и найти изгибающий момент в защемлении. Способ приравнивания перемещений заключается в том, что статически неопределимую балку мы заменяем статически определимой, загруженной реакциями от лишних отброшенных связей, и приравнивая к нулю перемещение в месте каждой отброшенной связи, получаем необходимое число дополнительных уравнений, связывающих между собой реакции и внешнюю нагрузку. Статически определимая балка, полученная таким образом называется основной системой.
Методические указания к выполнению расчетов обоими методами даны в подразделе 6.2. В подразделе 6.3. выполнен пример расчета многопролетной статически неопределимой балки. Методические указания Определение лишних неизвестных По теореме о трех моментах 1. Основную систему для расчета неразрезной балки получим, если над всеми промежуточными опорами и в местах защемлений ее концов «врезать» шарниры, а также ввести со стороны защемлений фиктивные пролеты длиною равной нулю, т.е. расчленить неразрезную балку на отдельные двухопорные балки, а в качестве «лишних» неизвестных принять внутренние изгибающие моменты в надопорных сечениях Мn – неизвестные опорные моменты в сечениях неразрезной балки над опорами. 2. Для каждой двухопорной балки построить эпюры изгибающих моментов от заданной внешней нагрузки, вычислить площади эпюр на каждом пролете w i и найти положение их центров тяжести. 3. Составить уравнения трех моментов для каждых двух смежных пролетов. Для любых смежных пролетов уравнение трех моментов имеет вид
Здесь wnи w n + 1 – площади эпюр моментов от заданных нагрузок соответственно в nиn+1 пролетах, рассматриваемых как двухопорныешарнирно опертые балки; а n – расстояние от центра тяжести «грузовой» площади wn до левой опоры n-1; b n+1– расстояние от центра тяжести «грузовой» площади wn + 1 до правой опоры n+1 (рис.12). 4. Решить систему составленных уравнений, найти опорные моменты на промежуточных опорах и в местах защемлений концов балки (если такие закрепления имеются). Найти опорные моменты на крайних опорах при наличии консолей, используя метод сечений, как для статически определимой балки.
Рис. 12 5. Рассматривая отдельные двухопорные балки, на которые была расчленена неразрезная балка, нагруженные уже известными опорными моментами и заданной нагрузкой, найти опорные реакции для каждой из указанных балок. Затем по ним определить опорные реакции неразрезной балки, суммируя реакции на промежуточных опорах от двух смежных пролетов. Опорные реакции неразрезной балки можно вычислить и иначе. Сумму моментов всех сил слева или справа от первой промежуточной опоры, относительно этой опоры, приравнять значению опорного момента и определить опорную реакцию на крайней левой или правой опоре неразрезной балки. Затем рассмотреть два левых или правых пролета. Сумму моментов всех сил слева или справа относительно второй промежуточной опоры приравнять величине опорного момента на этой опоре. Подставить уже известные значения реакции на крайней левой или правой опоре неразрезной балки и произвести вычисление опорной реакции на первой промежуточной опоре левой или правой и по аналогии определить все опорные реакции неразрезной балки. Произвести контроль правильности вычисления опорных реакций неразрезной балки åU=0.
6. Построить эпюры поперечных сил и изгибающих моментов для каждой однопролетной балки как от сил, непосредственно приложенных к балке, так и от опорных моментов. 7. Построить суммарные эпюры поперечных сил и изгибающих моментов, т.е. эпюры для заданной неразрезной балки, соединив эпюры однопролетных балок. Эпюру поперечных сил для неразрезной балки можно построить и иначе, т.е. после определения опорных реакций вычислить ординаты в характерных точках по методу сечений как сумму сил по одну сторону от сечения или по формуле в пределах каждого пролета
Здесь Q0 – поперечная сила в сечении Z простой двухопорной балки от заданной нагрузки. Мn и Мn - 1 – опорные моменты на левой и правой опоре данного пролета неразрезной балки. Эпюру изгибающих моментов для неразрезной балки можно так же построить и иначе, т.е. после определения опорных реакций, вычислить ординаты в характерных точках по методу сечений как сумму моментов сил по одну сторону от сечения, или алгебраически сложить в каждом пролете эпюры опорных моментов и эпюры изгибающих моментов от заданной нагрузки однопролетных балок основной системы, или по формуле в пределах каждого пролета
Здесь М0 – изгибающий момент в сечении Z простой двухопорной балки от заданной нагрузки. 8. Подобрать двутавровое сечение балки из условия прочности по нормальным напряжениям
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 676; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.163.26 (0.007 с.) |

 (6.2.1)
(6.2.1)
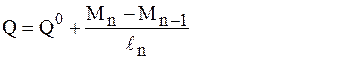 (6.2.2)
(6.2.2) (6.2.3)
(6.2.3)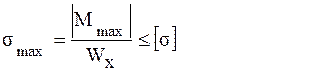 (6.2.4)
(6.2.4)


