
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к расчетуСодержание книги
Поиск на нашем сайте
Внецентренно нагруженных стержней 1. Следует определить геометрические характеристики поперечного сечения стержня – площадь F, координаты ее центра тяжести относительно начальных осей хс и ус и квадраты радиусов инерции относительно главных центральных осей Определяются F по известным линейным размерам сечения и квадратам радиусов инерции по формулам
где Jx, Jy - моменты инерции относительно главных центральных осей. Способ вычисления положения центров тяжести площади сечения и вычисление моментов инерции для сложных фигур представлен в разделе 3. 2. Определить положение нейтральной линии, т.е. линии, на которой нормальные напряжения будут равны нулю. Из формулы (7.1.1) следует, что это будет прямая линия, уравнение для которой будет иметь вид 1 + Провести нейтральную линию на чертеже сечения можно, вычислив координаты точек пересечения этой линией главных центральных осей по формулам (7.2.3), полученным из уравнения (7.2.2) у0 = 3. Наибольшие по модулю напряжения будут в наиболее удаленной от нейтральной оси в точке А (рис. 19). Подставив координаты этой точки в формулу (7.1.1), получим значение максимальных но модулю напряжений, а сравнив их с допускаемыми проверим прочность стержня. Если точка приложения силы находится за пределами ядра сечения, то в сечении стержня возникают напряжения разных знаков. (Ядром сечения называется область вокруг центра тяжести сечения, отличающегося тем, что сила, приложенная в пределах этой области, вызывает напряжения только одного знака во всем сечении). Так как материал стержня может иметь разные допускаемые нормальные напряжения для растяжения и сжатия, то прочность следует проверять для обоих случаев по условиям:
│σс│max ≤ [σc]; σPmax ≤ [σp] (7.2.4) Наибольшие по модулю напряжения противоположного, по сравнению с действующими в точке А, знака будут находиться в наиболее удаленной точке В по другую сторону от нейтральной оси. Подставив координаты точки В в уравнение (7.1.1) получим максимальные по модулю напряжения другого знака. 4. Нормальные напряжения в сечении будут изменяться по линейному закону от максимальных по модулю напряжений в точке А, через ноль на уровне нейтральной оси, до максимальных напряженийно модулю другого знака в точке В.
5. Допустимую нагрузку, которую может выдержать стержень, определяем по формулам: P ≤
P ≤
где [σ]А, [σ]В – допускаемые напряжения в точках А и В соответственно на растяжение и сжатие. За действительную допускаемую нагрузку принимается меньшая из двух, полученных по формулам (7.2.5а и 7.2.5б). Пример расчета стержня на внецентренное сжатие Короткий чугунный стержень, поперечное сечение которого показано на рис. 18, загружен в точке А продольной сжимающей силой Р. Найти положение нулевой линии и построить эпюру нормальных напряжений. Определить допустимую нагрузку Р из условий прочности в опасных точках сечения стержня.
Рис. 18 Рис. 19 Даны геометрические размеры поперечного сечения стержня а = 8 см, a b = 10 см, а также допускаемые напряжения чугуна на сжатие [σс]= 120 МПа и на растяжение [σр]= 30 МПа. Определение геометрических характеристик поперечного сечения стержня. Площадь F = 3 a · 2b + a · b = 24 · 20 + 8 · 10 = 560 см2 Сечение стержня симметрично относительно оси у, поэтому эта ось является главной центральной. Положение второй главной центральной оси найдем, если определим положение центра тяжести сечения на оси у. За начальную ось х примем ось, совпадающую с нижней гранью сечения, тогда координаты центра тяжести будут yc = = где статический момент Главные моменты инерции Jx =
Jу = Квадраты радиусов инерции
2. Определение положения нулевой линии (рис. 19) х0 = у0 = Здесь хр и ур - координаты точки приложения нагрузки Р. 3. Вычисление напряжений в опасных точках Опасными точками являются наиболее удаленные от нулевой линии точки А и В поперечного сечения стержня. Вычислим напряжение в этих точках в функции от нагрузки Р.
= –
= По этим значениям на рис. 19 построена в масштабе эпюра а. 4. Определение допустимой нагрузки Р из условий прочности. Условие прочности для точки А, где действует наибольшее сжимающее напряжение │σА│≤ [σС] или Отсюда Р ≤ Условие прочности для точки В, где возникает наибольшее растягивающее напряжение
│σВ│≤ [σР] или
Отсюда Р ≤ Окончательно принимаем допустимую нагрузку Р = 428кН.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.131.225 (0.008 с.) |

 и
и  .
. ,
, 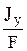 (7.2.1)
(7.2.1) = 0 (7.2.2)
= 0 (7.2.2) ; х0 =
; х0 =  (7.2.3)
(7.2.3)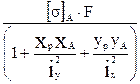 (7.2.5а)
(7.2.5а) (7.2.5б)
(7.2.5б)
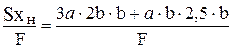 =
= cм
cм =
=  .
.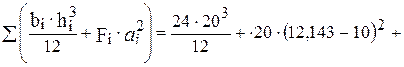
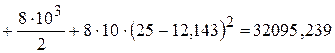 см4,
см4, 23466,667 см4
23466,667 см4 = 57,313 см2,
= 57,313 см2, = 41,905 см2.
= 41,905 см2. –
–  = –10,476 см,
= –10,476 см, –
–  = –3,210 см.
= –3,210 см.
 ,
,
 .
. ≤ [σС]
≤ [σС] =
=  = 9674,63 · 102 Н = 976 кН
= 9674,63 · 102 Н = 976 кН ≤ [σР]
≤ [σР]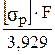 =
=  = 4275,90 · 102 Н = 428 кН
= 4275,90 · 102 Н = 428 кН


