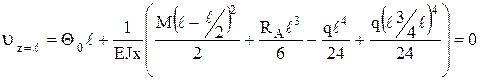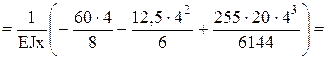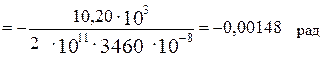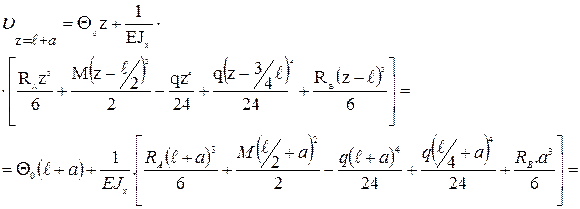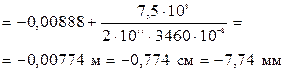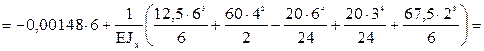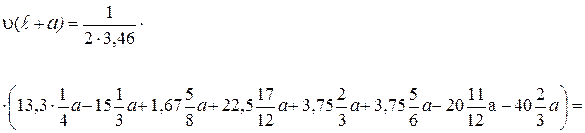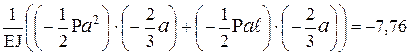Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет перемещений в балках при плоскомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Поперечном изгибе Общие пояснения Перемещения в балках оцениваются прогибом центра тяжести поперечного сечения балки vк и углом поворота сечения Qк вокруг оси перпендикулярной плоскости изгиба и проходящей через центр тяжести сечения. Достаточно большое число способов определения перемещений в балках можно разделить на две группы. К первой группе относятся способы нахождения аналитических функций перемещений путем интегрирования приближенного дифференциального уравнения изогнутой оси балки Далее в подразделе 5.2. даны методические указания для определения перемещений наиболее продуктивным методом первой группы – методом начальных параметров, и второй группы – способом А.К.Верещагина для вычисления интеграла Максвелла-Мора. В подразделе 5.3. приведен пример расчета перемещений балки двумя упомянутыми методами. Методические указания 1. При определении углов поворота и прогибов сечений балки методом начальных параметров применяются универсальные уравнения в виде:
Здесь Θ0 и u0 – угол поворота и прогиб сечения в начале координат; М, Р, q – соответственно сосредоточенные моменты, силы и равномерно распределенные нагрузки, приложенные к балке; Z – расстояние от начала координат до рассматриваемого сечения, угол поворота u¢ и прогиб u которого определяется; а, в, с – расстояние от начала координат до точки приложения соответственно М, Р, q. Эти уравнения можно применять на любом участке балки, при этом в каждом частном случае в уравнение войдут те члены, которые соответствуют нагрузкам, расположенным между началом координат (в крайней левой точке балки) и заданным сечением. Если направление действия нагрузок будет отвечать отрицательному изгибающему моменту, то знаки перед соответствующими членами меняются с плюса на минус. Постоянные EJxu0 и EJхΘ0 определяются из условий опорных закреплений балки. Если распределенная нагрузка q не доходит до заданного сечения в пределах данного участка, то необходимо эту нагрузку продолжить до конца данного участка и одновременно ввести компенсирующую нагрузку другого знака заданной интенсивности на той же части балки.
Интегрирование уравнения
производить без раскрытия скобок. 2. Применить формулу Верещагина при вычисления углов поворота и прогибов сечений балки интегралом Мора:
где d – обобщенное перемещение поперечного сечения (угол поворота или прогиб); wpi – площади эпюры изгибающих моментов от заданной нагрузки.
Площади простых фигур и координаты центров тяжести этих площадей приведены в таблице 1. Площади wi и ординаты 3. Строить изогнутую ось балки (упругую линию) следует по вычисленным значениям прогибов и углов поворота сечений. Упругая балка обращена выпуклостью вниз там, где изгибающий момент положительный, и выпуклостью вверх там, где М – отрицательный. Нулевым точкам эпюры М соответствуют точки перегиба упругой линии. Пример расчета Построить эпюры поперечных сил Q и изгибающих моментов М. Подобрать по сортаменту двутавровое сечение балки из условия прочности по нормальным напряжениям, если [s] = 160мПа. Вычислить методом начальных параметров прогиб посередине пролета Вычислить интегралом Мора по способу Верещагина углы поворота на опорах Θz=0 и Θz=
Вычертить изогнутую ось балки (масштаб: длины 1:50, прогиба 1:1). Выяснить, как следует изменить одну из нагрузок, чтобы: а) на одной из опор угол поворота сечения стал равным нулю; б) прогиб конца консоли стал равным нулю.
Определяем опорные реакции:
Проверка
0≡0 Реакции определены правильно.
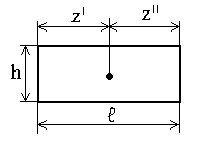
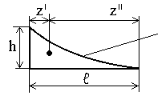
Таблица 1
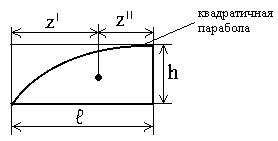
Примечание: в отмеченных (*) случаях h3 = h, если равномерно распределенная нагрузка на участке длиной ℓ у балки одинакова.
2. Построение эпюры поперечных сил Q. 1-й и 2-й участок:
Определим координату Z, при которой изгибающий момент на участке 1 будет экстремальным:
4-й участок. Консоль: Q = P = 20 кН. 3-й участок: Q = P – RВ = 20 – 67,5 = – 47,5 кН. 3. Построить эпюры изгибающих моментов М.
Эпюры Q и M показаны на рис. 10б и в. 4. Подбор сечения двутавровой балки из условия прочности при изгибе
Тогда требуемый момент сопротивления
Принимаем двутавр № 24, у которого Wх = 289 см3, Jх = 3460 см4. Действительное нормальное напряжение
Расхождение в процентах
5. Вычисление методом начальных параметров прогибов и углов поворота сечений балки.
Изгибающий момент М(z), угол поворота Θ(z) и прогиб u(z) будут
В нашем примере u0 = 0, так как начало координат совпадает с опорой А, где прогиб равен нулю. Θ0 определим из опорного условия, что прогиб на опоре В равен нулю:
Тогда
6.
Прогиб посередине пролета
7.
Прогиб на конце консоли
8. Угол поворота на опоре В
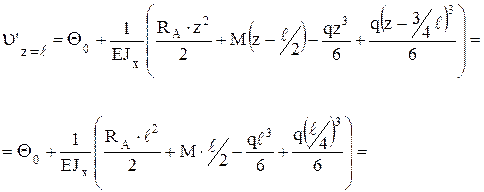
9. Вычисление перемещений интегралом Мора по способу Верещагина. Для вычисления перемещений предварительно выполняется разбивка площади грузовой эпюры изгибающих моментов на простые составляющие и строятся эпюры изгибающих моментов от единичной обобщенной силы, приложенной в сечении, где определяется соответствующее перемещение. На этих эпюрах указываются значения изгибающих моментов от единичной обобщенной силы под центром тяжести каждой составляющей площади грузовой эпюры изгибающих моментов. Перечисленные эпюры представлены на рис. 11.
Рис. 11 Составляющие площади грузовой эпюры, представленные на рис. 11а будут:
Прогиб u(ℓ/2) с учетом ординат на рис. 11б будет:
Угол поворота на опоре А, Θ(0), с учетом ординат на рис. 11 г будет:
Угол поворота на опоре В, Θ(ℓ), с учетом ординат на рис. 11д будет:
Результаты расчетов перемещений (углов поворота и прогибов) практически совпадают при расчете метода начальных параметров и с использованием правила Верещагина для вычисления интеграла Максвела-Мора. Изогнутая ось балки представлена на рис. 10. Как видно из рисунка, она хорошо согласуется с эпюрой изгибающих моментов, представленной на рис. 10в.
10. Исключение угла поворота на опоре А можно добиться, изменив заданный момент М. Величину изменения момента ΔМ можно определить из условия, что при действии дополнительного момента угол поворота будет равен ранее найденному но с обратным знаком. Тогда
или 
Таким образом, чтобы угол поворота на опоре был равен 0, надо изгибающий момент увеличить на 30,5 кНм. 11. Исключение прогиба на конце консоли можно добиться, изменив заданную силу Р. Величину изменения силы ΔР можно определить из условия, что при действии на балку дополнительной силы ΔР прогиб на конце консоли от нее будет равен ранее найденному, но с обратным знаком.
Тогда
или
Таким образом, чтобы прогиб на концах консоли был равен 0 следует силу Р уменьшить на 6,7 кН.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.23.94 (0.009 с.) |

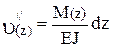 . Ко второй группе относятся энергетические способы нахождения перемещений в заданных точках, например, путем вычисления интеграла Максвелла-Мора
. Ко второй группе относятся энергетические способы нахождения перемещений в заданных точках, например, путем вычисления интеграла Максвелла-Мора  где M0(z) – изгибающий момент от единичной обобщенной силы, приложенной к точке, где определяются соответствующие перемещения.
где M0(z) – изгибающий момент от единичной обобщенной силы, приложенной к точке, где определяются соответствующие перемещения. (5.2.1)
(5.2.1)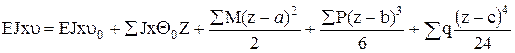 (5.2.2)
(5.2.2) (5.2.3)
(5.2.3) (5.2.4)
(5.2.4) – ординаты эпюр изгибающих моментов от единичных сил Рi= 1 или от единичных моментов Мi= 1, приложенных в сечениях, где вычисляем прогиб или угол поворота, под центром тяжести площадей wpi.
– ординаты эпюр изгибающих моментов от единичных сил Рi= 1 или от единичных моментов Мi= 1, приложенных в сечениях, где вычисляем прогиб или угол поворота, под центром тяжести площадей wpi. , если Е = 2×105 МПа, сравнить его с допускаемым
, если Е = 2×105 МПа, сравнить его с допускаемым 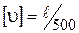 и, если нужно, увеличить номер балки, а так же углы поворота на опорах Θz= 0 и Θz=
и, если нужно, увеличить номер балки, а так же углы поворота на опорах Θz= 0 и Θz=  и прогиб на конце консоли υz=ℓ+ а .
и прогиб на конце консоли υz=ℓ+ а . и на конце консоли
и на конце консоли  .
.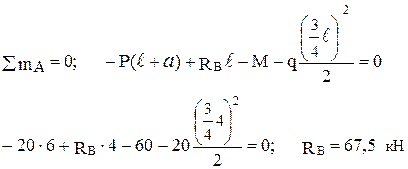


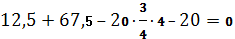

 квадратичная
парабола
квадратичная
парабола





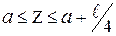


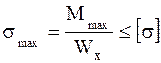

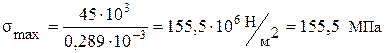
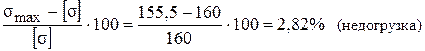


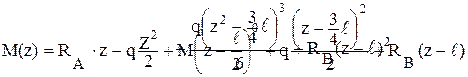
 При составлении уравнения для М(z), считается, что равномерно распределенная нагрузка q действует до конца балки, а на участке, где она отсутствовала, приложена нагрузка q противоположного знака, как это показано пунктиром на рис. 10а.
При составлении уравнения для М(z), считается, что равномерно распределенная нагрузка q действует до конца балки, а на участке, где она отсутствовала, приложена нагрузка q противоположного знака, как это показано пунктиром на рис. 10а.