
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перемещение в системе координатСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Когда мы говорим о перемещении, важно помнить, что перемещение зависит от системы отсчета, в которой рассматривается движение. Обратите внимание на рисунок.
Рис. 4. Определение модуля перемещения тела
Тело движется в плоскости XOY. Точка А – начальное положение тела. Ее координаты А(х1; у1). Тело перемещается в точку В (х2; у2). Вектор Рассчитать его можно как гипотенузу прямоугольного треугольника АВС, используя теорему Пифагора: АВ2 = АС2 + ВС2. Тема: Законы взаимодействия и движения тел Урок 3. Определение координаты движущегося тела Ерюткин Евгений Сергеевич
Тема урока – «Определение координаты движущегося тела». Мы уже обсуждали характеристики движения: пройденный путь, скорость и перемещение. Главной характеристикой движения является местоположение тел. Чтобы его характеризовать, необходимо использовать понятие «перемещение», именно оно дает возможность определить местоположение тела в любой момент времени, именно в этом и состоит главная задача механики.
Рис. 1. Путь как сумма множества прямолинейных перемещений
Траектория как сумма перемещений На рис. 1 представлена траектория движения тела из точки А в точку В в виде кривой линии, которую можем представить как набор малых перемещений. Перемещение – это вектор, следовательно, весь пройденный путь мы можем представить как набор сумм очень малых перемещений вдоль кривой. Каждое из малых перемещений – это прямая линия, все вместе они составят всю траекторию. Обратите внимание:- именно перемещение определяет положение тела. Любое перемещение мы должны рассматривать в определенной системе отсчета. Координаты тела Рисунок надо совместить с системой отсчета движения тел. Самый простой из рассматриваемых нами способов – это движение по прямой, вдоль одной оси. Для характеристики перемещений будем использовать способ, связанный с системой отсчета – с одной линией; движение прямолинейное.
Рис. 2. Одномерное движение
На рис. 2 представлена ось ОХ и случай одномерного движения, т.е. тело движется вдоль прямой, вдоль одной оси. В данном случае тело переместилось из точки А в точку В, перемещение составил вектор АВ. Для определения координаты точки А мы должны сделать следующее: опустить перпендикуляр на ось, координата точки А на этой оси будет обозначаться Х1, а опустив перпендикуляр из точки В, получим координату конечной точки – Х2. Выполнив это, можно говорить о проекции вектора на ось ОХ. При решении задач нам будет нужна проекция вектора, скалярная величина. Проекция вектора на ось В первом случае вектор направлен вдоль оси ОХ, совпадает по направлению, поэтому проекция будет со знаком плюс.
Рис. 3. Проекция перемещения со знаком минус
Пример отрицательной проекции На рис. 3 изображена еще одна возможная ситуация. Вектор АВ в данном случае направлен против выбранной оси. В этом случае проекция вектора на ось будет иметь отрицательное значение. При вычислении проекции обязательно ставится символ вектора S, а внизу – индекс Х: Sx. Путь и перемещение при прямолинейном движении Прямолинейное движение является простым видом движения. В данном случае можно говорить, что модуль проекции вектора – это и будет пройденный путь. Следует обратить внимание, что в данном случае длина модуля вектора равна пройденному пути.
Рис. 4. Пройденный путь совпадает с проекцией перемещения
Примеры различной взаимной ориентации оси и перемещения Чтобы окончательно разобраться с вопросом проекции вектора на ось и с координатами, рассмотрим несколько примеров:
Рис. 5. Пример 1
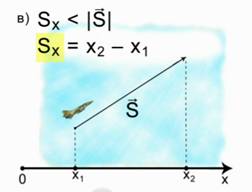
Пример 1. Модуль перемещения равен проекции перемещения и определяется как Х2 – Х1, т.е. из конечной координаты вычитаем начальную.
Рис. 6. Пример 2
Пример 2. Очень любопытен второй рисунок под буквой Б. Если тело движется перпендикулярно выбранной оси, то координата тела на этой оси не изменяется, и в этом случае модуль перемещения по этой оси равен 0.
Рис 7. Пример 3
Пример 3. Если тело движется под углом к оси ОХ, то, определяя проекцию вектора на ось ОХ, видно, что проекция по своему значению будет меньше, чем сам модуль вектора S. Путем вычитания Х2 – Х1, определяем скалярное значение проекции. Решение задачи на определение пути и перемещения Рассмотрим задачу. Определить местоположение моторной лодки. Лодка отошла от пристани и прошла вдоль берега прямолинейно и равномерно сначала 5 км, а затем в обратном направлении еще 3 км. Необходимо определить пройденный путь и модуль вектора перемещения.
Тема: Законы взаимодействия и движения тел Урок 4. Перемещение при прямолинейном равномерном движении Ерюткин Евгений Сергеевич Равномерное прямолинейное движение Для начала, давайте вспомним определение равномерного движения. Определение: равномерным движением называется такое движение, при котором тело за любые равные промежутки времени проходит одинаковые расстояния. Необходимо отметить то, что равномерным может быть не только прямолинейное, но и криволинейное движение. Сейчас мы рассмотрим один частный случай – движение вдоль прямой. Итак, равномерное прямолинейное движение (РПД) – движение, при котором тело движется вдоль прямой и за любые равные промежутки времени совершает одинаковые перемещения. Скорость Важная характеристика такого движения – скорость. Из 7 класса вам известно, что скорость – это физическая величина, которая характеризует быстроту движения. При равномерном прямолинейном движении скорость – величина постоянная. Скорость величина векторная, обозначается
в зависимости от ее направления
Обратите внимание на рис. 1. Если вектор скорости направлен по направлению оси, то тогда проекция скорости будет Определение скорости, пути и перемещения Перейдем к формуле для расчета скорости. Скорость определяется как отношение перемещения ко времени, в течение которого это перемещение произошло: Обращаем ваше внимание на то, что при прямолинейном движении длина вектора перемещения равна пути пройденному этим телом. Поэтому мы можем сказать, что модуль перемещения равен пройденному пути. Чаще всего вы эту формулу встречали в 7 классе и в математике. Она записывается просто: S = V * t. Но важно понимать, что это лишь частный случай. Уравнение движения Если вспомнить, что проекция вектора определяется как разность конечной координаты и начальной координаты, т.е. Sx= х2 – х1, то можно получить закон движения при прямолинейном равномерном движении.
График скорости Обратите внимание, что проекция скорости может быть как отрицательной, так и положительной, поэтому здесь ставится плюс или минус, в зависимости от направления скорости относительно выбранной оси.
Рис. 2. График зависимости проекции скорости от времени для РПД
График зависимости проекции скорости от времени, представленный выше, непосредственная характеристика равномерного движения. По горизонтальной оси откладывается время, по вертикальной оси – скорость. Если график проекции скорости располагается над осью абсцисс, то это означает, что тело будет двигаться вдоль оси Ох, в положительном направлении. В противоположном случае направление движения не совпадает с направлением оси. Геометрическое толкование пути
Рис. 3. Геометрический смысл графика скорости от времени
Тема: Законы взаимодействия и движения тел Урок 5. Прямолинейное равноускоренное движение. Ускорение Ерюткин Евгений Сергеевич
Тема урока «Неравномерное прямолинейное движение, прямолинейное равноускоренное движение». Для описания такого движения мы введем важную величину – ускорение. Напомним, что на предыдущих занятиях мы обсуждали вопрос о прямолинейном равномерном движении, т.е. таком движении, когда скорость остается величиной постоянной. Неравномерное движение А если скорость изменяется, что тогда? В этом случае говорят о том, что движение неравномерное. Мгновенная скорость Для характеристики неравномерного движения вводится новая физическая величина – мгновенная скорость. Определение: мгновенная скорость – это скорость тела в данный момент или в данной точке траектории. Прибор, который показывает мгновенную скорость, есть на любом движущемся средстве: в автомобиле, поезде и т.д. Это прибор, который называется спидометр (от англ. – speed («скорость»)). Обращаем ваше внимание на то, что мгновенная скорость определяется как отношение перемещения ко времени, в течение которого это перемещение произошло. Но ведь это определение ничем не отличается от данного нами ранее определения скорости при РПД. Для более точного определения необходимо отметить, что промежуток времени и соответствующее ему перемещение берутся очень маленькими, стремящимися к нулю. Тогда скорость не успевает поменяться сильно, и мы можем пользоваться формулой, которую вводили ранее: Обратите внимание на рис. 1. х0 и х1 – это координаты вектора перемещения. Если этот вектор будет очень маленьким, то и изменение скорости произойдет достаточно быстро. Это изменение в данном случае мы характеризуем изменением мгновенной скорости.
Рис. 1. К вопросу об определении мгновенной скорости
Ускорение Таким образом, неравномерное движение имеет смысл характеризовать изменением скорости от точки к точке, тем, как быстро это происходит. Это изменение скорости характеризуется величиной, которая называется ускорение. Обозначается ускорение Определение: ускорение определяется как отношение изменения скорости ко времени, в течение которого это изменение произошло. Ускорение измеряется м/с2. По сути, скорость изменения скорости – это есть ускорение. Значение проекции ускорения, поскольку это вектор, может быть отрицательным и положительным. Важно отметить, что, куда направлено изменение скорости, туда будет направлено ускорение. Особое значение это приобретает при криволинейном движении, когда изменяется значение. Тема: Законы взаимодействия и движения тел Урок 6. Скорость прямолинейного равноускоренного движения. График скорости Ерюткин Евгений Сергеевич Ускорение Вспомним, что такое ускорение. Ускорение – это физическая величина, которая характеризует изменение скорости за определенный промежуток времени. то есть ускорение – это величина, которая определяется изменением скорости за время, в течении которого это изменение произошло. Уравнение скорости Воспользовавшись уравнением, определяющим ускорение, удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени: Это уравнение даёт возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО. График скорости График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.
Рис. 1. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения
Проанализируем различные графики. Первый. Уравнение проекции скорости: Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит: График начинается в точке Если вы внимательно посмотрите на уравнение скорости, то вспомните, что в математике была похожая функция. Некоторые частные случаи Чтобы окончательно разобраться с графиком скорости рассмотрим частный случай. На первом графике зависимость скорости от времени связана с тем, что начальная скорость, Запись этого уравнения
Рис. 2. Различные случаи равноускоренного движения Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси ОХ. Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси ОХ. При этом модуль скорости постоянно возрастает, тело ускоряется. Данный видеоурок поможет пользователям получить представление о теме «Перемещение при прямолинейном равноускоренном движении». В ходе этого занятия учащиеся смогут расширить свои знания о прямолинейном равноускоренном движении. Учитель расскажет, как правильно определять перемещение, координаты и скорость при таком движении. Тема: Законы взаимодействия и движения тел Урок 7.Перемещение при прямолинейном равноускоренном движении Ерюткин Евгений Сергеевич
На предыдущих уроках мы обсуждали, как определить пройденный путь при равномерном прямолинейном движении. Настало время узнать, как определить координату тела, пройденный путь и перемещение при прямолинейном равноускоренном движении. Это можно сделать, если рассмотреть прямолинейное равноускоренное движение как набор большого количества очень малых равномерных перемещений тела. Опыт Галилея Первым решил задачу местоположения тела в определённый момент времени при ускоренном движении итальянский учёный Галилео Галилей. Свои опыты он проводил с наклонной плоскостью. По желобу он запускал шар, мушкетную пулю, а затем определял ускорение этого тела. Как же он это делал? Он знал длину наклонной плоскости, а время определял по биению своего сердца или по пульсу. Определение перемещения по графику скорости Рассмотрим график зависимости скорости равноускоренного прямолинейного движения от времени. Эта зависимость вам известна, она представляет собой прямую линию: v = v0 + at
Рис.1. Определение перемещения при равноускоренном прямолинейном движении
График скорости разбиваем на маленькие прямоугольные участки. Каждый участок будет соответствовать определённой постоянной скорости. Надо определить пройденный путь за первый промежуток времени. Запишем формулу: Теперь посчитаем суммарную площадь всех имеющихся у нас фигур. А сумма площадей при равномерном движении – это полный пройденный путь. Обратите внимание, от точки к точке скорость будет изменяться, тем самым мы получим путь, пройденный телом именно при прямолинейном равноускоренном движении. Заметим, что при прямолинейном равноускоренном движении тела, когда скорость и ускорение направлены в одну сторону, модуль перемещения равен пройденному пути, поэтому, когда мы определяем модуль перемещения – определяем пройденный путь. В данном случае можем говорить, что модуль перемещения будет равен площади фигуры, ограниченной графиком скорости и времени. Воспользуемся математическими формулами для вычисления площади указанной фигуры.
Конечную скорость, рассмотренную на предыдущем уроке, мы можем записать как сумму начальной скорости и вклада, обусловленного наличием у тела постоянного ускорения. Получается выражение:
Если открыть скобки, то
Если по отдельности записать каждое из этих выражений, итогом будет следующее:
Это уравнение впервые было получено благодаря экспериментам Галилео Галилея. Поэтому можно считать, что именно этот ученый впервые дал возможность определить местоположение тела в любой момент. Это и есть решение главной задачи механики. Определение координаты тела Теперь давайте вспомним, что пройденный путь, равный в нашем случае модулю перемещения, выражается разностью: Если в уравнение Галилея подставить полученное нами выражение для S, то запишем закон, по которому движется тело при прямолинейном равноускоренном движении:
Следует помнить, что скорость, ее проекция и ускорение могут быть отрицательными. Следующим этапом рассмотрения движения станет исследование движения по криволинейной траектории.
Тема: Законы взаимодействия и движения тел Урок 8. Перемещение тела при прямолинейном равноускоренном движении без начальной скорости Ерюткин Евгений Сергеевич Прямолинейное равноускоренное движение Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в XVI веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путем. Формула выглядит следующим образом: S=Vot+ at2/2, где а – это ускорение. Случай равномерного движения Первый, самый простой случай, это ситуация, когда ускорение равно нулю. Это означает, что уравнение, приведенное выше, превратится в уравнение: S = V0t. Это уравнение дает возможность найти пройденный путь равномерного движения. S, в данном случае, является модулем вектора. Его можно определить как разность координат: конечная координата х минус начальная координата х0. Если подставить это выражение в формулу, то получается зависимость координаты от времени. Случай движения без начальной скорости Рассмотрим вторую ситуацию. При V0 = 0 начальная скорость равна 0, это значит, что движение начинается из состояния покоя. Тело покоилось, затем начинает приобретать и увеличивать скорость. Движение из состояния покоя будет записываться без начальной скорости: S = at2/2. Если S – модуль перемещения (или пройденный путь) обозначить как разность начальной и конечной координаты (из конечной координаты вычитаем начальную), то получится уравнение движения, которое дает возможность определить координату тела для любого момента времени: х = х0 + at2/2. Проекция ускорения может быть, как отрицательной, так и положительной, поэтому можно говорить о координате тела, которая может как увеличиваться, так и уменьшаться. Пропорциональность пути квадрату времени Важные закономерности уравнений без начальной скорости, т.е. когда тело начинает свое движение из состояния покоя: Sx – пройденный путь, он пропорционален t2, т.е. квадрату времени. Если рассматривать равные промежутки времени – t1, 2t1, 3t1, то можно заметить следующие соотношения: Sx ~ t2 S1 ~ 1 S1 = a/2*t12 S2 ~ 4 S2 = a/2*(2t1)2 S3 ~ 9 S3 = a/2*(3t1)2 Если продолжить, закономерность сохранится. Перемещения за последовательные промежутки времени Можно сделать следующее заключение: пройденные расстояния увеличиваются пропорционально квадрату увеличения промежутков времени. Если был один промежуток времени, например 1 с, значит, пройденный путь будет пропорционален 12. Если второй отрезок 2 с, то пройденное расстояние будет пропорционально 22, т.е. = 4. Если за единицу времени выбираем некий промежуток, то полные расстояния, пройденные телом за последующие равные промежутки времени, будут относиться как квадраты целых чисел. Иными словами, перемещения, совершенные телом за каждую последующую секунду, будут относиться как нечетные числа: S1:S2:S3:…:Sn=1:3:5:…:(2n-1)
Рис. 1. Перемещения за каждую секунду относятся как нечетные числа
Рассмотренные закономерности на примере задачи Исследованные два очень важных заключения свойственны только прямолинейному равноускоренному движению без начальной скорости. Задача: автомобиль начинает двигаться от остановки, т.е. из состояния покоя, и за 4 с своего движения проходит 7 м. Определите ускорение тела и мгновенную скорость через 6 с после начала движения.
Рис. 2. Решение задачи
Решение: автомобиль начинает движение из состояния покоя, следовательно, путь, который проходит автомобиль, рассчитывается по формуле: S = at2/2. Мгновенная скорость определяется как V = at. S4 = 7 м, расстояние, которое автомобиль прошел за 4 с своего движения. Его можно выразить как разность полного пути, пройденного телом за 4 с, и пути, пройденного телом за 3 с. Используя это, получаем ускорение а = 2 м/с2, т.е. движение ускоренное, прямолинейное. Чтобы определить мгновенную скорость, т.е. скорость в конце 6 с, следует ускорение умножить на время, т.е. на 6 с, во время которых тело которое продолжало двигаться. Получаем скорость v(6с) = 12 м/с. Ответ: модуль ускорения равен 2 м/с2; мгновенная скорость в конце 6 с равна 12 м/с.
Тема: Законы взаимодействия и движения тел Урок 9: Лабораторная работа №1 «Исследование равноускоренного движения без начальной скорости» Ерюткин Евгений Сергеевич Цель работы Цель лабораторной работы – определить ускорение движения тела, а также его мгновенную скорость в конце движения. Впервые данную лабораторную работу проводил Галилео Галилей. Именно благодаря данной работе Галилею удалось установить опытным путём ускорение свободного падения. Наша задача – рассмотреть и разобрать, как можно определить ускорение при движении тела по наклонному жёлобу. Оборудование Оборудование: штатив с муфтой и лапкой, в лапке укреплён наклонный жёлоб; в жёлобе располагается упор в виде металлического цилиндра. Движущееся тело – это шарик. Счётчик времени – метроном, если его запустить, он будет считать время. Измерительная лента понадобится для измерения расстояния.
Рис. 1. Штатив с муфтой и лапкой, желоб и шарик
Рис. 2. Метроном, цилиндрический упор
Таблица измерений Составим таблицу, состоящую из пяти столбцов, каждый из которых необходимо заполнить. Первый столбец – это число ударов метронома, который используется нами как счетчик времени. S – следующий столбец – это расстояние, которое проходит тело, шарик, скатывающийся по наклонному жёлобу. Далее – время движения. Четвёртый столбец – это вычисленное ускорение движения. В последнем столбце – мгновенная скорость в конце движения шарика.
Необходимые формулы Для получения результата следует воспользоваться формулами: S = at2/2. Отсюда несложно получить, что ускорение будет равно отношению удвоенного расстояния, делённого на квадрат времени: a = 2S/t2. Мгновенная скорость определяется как произведение ускорения на время движения, т.е. промежутка времени от начала движения до того момента, как шарик столкнётся с цилиндром: V = at. Проведение эксперимента Перейдём к самому эксперименту. Для его выполнения следует отрегулировать метроном так, чтобы он совершал в одну минуту 120 ударов. Тогда между двумя ударами метронома будет промежуток времени, равный 0,5 с (полсекунды). Запускаем метроном и следим за тем, как он отсчитывает время. Далее при помощи измерительной ленты определяем расстояние между цилиндром, который составляет упор, и начальной точкой движения. Оно равно 1,5 м. Расстояние выбрано так, чтобы тело, скатывающееся по жёлобу, уложилось в промежуток времени не менее 4 ударов метронома.
Рис. 3. Постановка опыта
Опыт: шарик, который ставим в начало движения и отпускаем с одним из ударов, дает результат – 4 удара. Заполнение таблицы Результаты записываем в таблицу и переходим к вычислениям.
В первый столбец внесли цифру 3. Но ударов метронома было 4?! Первый удар соответствует нулевой отметке, т.е. мы начинаем отсчёт времени, поэтому время движения шарика – это промежутки между ударами, а их всего три. Длина пройденного пути, т.е. длина наклонной плоскости – 1,5 м. Подставляя эти значения в уравнение, получаем ускорение, равное приблизительно 1,33 м/с2. Обращаем ваше внимание, что это приближённое вычисление, с точностью до второго знака после запятой. Мгновенная скорость в момент удара равна приблизительно 1,995 м/с. Итак, мы выяснили, каким образом можно определить ускорение движущегося тела. Обращаем ваше внимание на то, что в своих опытах Галилео Галилей проводил определение ускорения, меняя угол наклона плоскости. Предлагаем вам самостоятельно проанализировать источники погрешностей при выполнении данной работы и сделать выводы.
Тема: Законы взаимодействия и движения тел Урок 10. Решение задач на определение ускорения, мгновенной скорости и перемещения при равноускоренном прямолинейном движении Ерюткин Евгений Сергеевич
Занятие посвящено решению задач на определение ускорения, мгновенной скорости и перемещения движущего тела. Задача на определение пути и перемещения Задача 1 посвящена исследованию пути и перемещения. Условие: тело движется по окружности, проходя ее половину. Необходимо определить отношение пройденного пути к модулю перемещения. Обратите внимание: дано условие задачи, но нет ни одного числа. Такие задачи будут встречаться в курсе физики довольно часто.
Рис. 1. Путь и перемещение тела
Введем обозначения. Радиус окружности, по которой движется тело, равен R. При решении задачи удобно сделать рисунок, на котором окружность и произвольную точку, из которой движется тело, обозначим А; тело движется в точку В, а S – это половина окружности, S Несмотря на то, что в задаче ни одного числа нет, тем не менее, в ответе мы получаем вполне определенное число (1,57).
Задача на график скорости Задача 2 будет посвящена графикам скорости. Условие: два поезда движутся навстречу друг другу по параллельным путям, скорость первого поезда – 60 км/ч, скорость второго – 40 км/ч. Ниже представлены 4 графика, и нужно выбрать те, на которых правильно изображены графики проекции скорости движения этих поездов.
Рис. 2. К условию задачи 2
Рис. 3. Графики к задаче 2
Ось скорости – вертикальная (км/ч), а ось времени – горизонтальная (время в ч). На 1-м графике две параллельные прямые, это модули скорости движения тела – 60 км/ч и 40 км/ч. Если вы посмотрите на нижний график, под номером 2, то увидите то же самое, только в отрицательной области: -60 и -40. На двух других графиках 60 сверху и -40 снизу. На 4-м графике 40 в верхней части, а -60 внизу. Что же можно сказать об этих графиках? Согласно условию задачи два поезда едут навстречу друг другу, по параллельным путям, поэтому если мы выберем ось, связанную с направлением скорости одного из поездов, то проекция скорости одного тела будет положительной, а проекция скорости другого отрицательной (поскольку сама скорость направлена против выбранной оси). Поэтому ни первый график, ни второй к ответу не подходят. Когда проекция скорости имеет одинаковый знак, нужно говорить о том, что два поезда движутся в одну сторону. Если мы выбираем систему отсчета, связанную с 1 поездом, то тогда величина 60 км/ч будет положительной, а величина -40 км/ч – отрицательной, поезд едет навстречу. Или наоборот, если мы связываем систему отчета со вторым поездом, то у одного из них проекция скорости 40 км/ч, а у другого -60 км/ч, отрицательная. Таким образом, подходят оба графика (3 и 4). Ответ: 3 и 4 графики. Задача на определение скорости при равнозамедленном движении Задача 3. Условие: автомобиль движется со скоростью 36 км/ч, и в течение 10 с тормозит с ускорением 0,5 м/с2. Необходимо определить его скорость в конце торможения В данном случае удобнее выбрать ось ОХ и направить начальную скорость вдоль этой оси, т.е. вектор начальной скорости будет направлен в ту же сторону, что и ось. Ускорение будет направлено в противоположную сторону, ведь автомобиль замедляет свое движение. Проекция ускорения на ось ОХ будет со знаком минус. Для нахождения мгновенной, конечной скорости воспользуемся уравнением проекции скорости. Запишем следующее: Vx= V0x- at. Подставляя значения, получаем конечную скорость 5 м/с. Значит, через 10 с после торможения скорость будет 5 м/с. Ответ: Vx = 5 м/с.
Задача на определение ускорения по графику скорости Задача 4. На графике представлены 4 зависимости скорости от времени, и необходимо определить, у какого из этих тел максимальное, а у какого минимальное ускорения.
Рис. 4. К условию задачи 4
Для решения необходимо рассмотреть все 4 графика поочередно. Для сравнения ускорений нужно определить их значения. Для каждого тела ускорение будет определяться как отношение изменения скорости ко времени, в течение которого это изменение произошло. Ниже проведены расчеты ускорения для всех четырех тел:
Как видим, у второго тела модуль ускорения минимальный, а у третьего тела – максимальный. Ответ: |a3| - max, |a2| - min.
Урок 11. Решение задач по теме «Прямолинейное равномерное и неравномерное движение» Ерюткин Евгений Сергеевич
Давайте рассмотрим две задачи, причем решение одной из них – в двух вариантах. Задача на определение пройденного пути при равнозамедленном движении Задача 1. Условие: самолет, летящий со скоростью 900 км/ч, совершает посадку. Время до полной остановки самолета 25 с. Необходимо определить длину взлетной полосы.
Рис. 1. К условию задачи 1
900 км/ч надо перевести в СИ, т.о. начальная скор
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 5767; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.9 (0.013 с.) |



 – это будет перемещение тела:
– это будет перемещение тела: 
 .
.






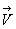 , единицей измерения скорости является м/с.
, единицей измерения скорости является м/с.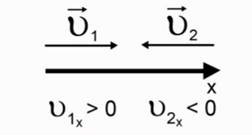 Рис. 1. Знак проекции скорости
Рис. 1. Знак проекции скорости . Если скорость
. Если скорость  направлена против выбранной оси, то проекция этого вектора
направлена против выбранной оси, то проекция этого вектора  будет отрицательной.
будет отрицательной. .
.


 .
.
 , это векторная величина.
, это векторная величина.
 ,
,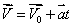

 . Скорость и время увеличиваются, обратите внимание, что на графике в том месте, где одна из осей – время, а другая – скорость, будет прямая линия. Начинается эта линия из точки
. Скорость и время увеличиваются, обратите внимание, что на графике в том месте, где одна из осей – время, а другая – скорость, будет прямая линия. Начинается эта линия из точки  , которая характеризует начальную скорость.
, которая характеризует начальную скорость. .
. продолжается до точки
продолжается до точки  , пересечения оси времени. В этой точке скорость тела становится равной нулю. Это означает, что тело остановилось.
, пересечения оси времени. В этой точке скорость тела становится равной нулю. Это означает, что тело остановилось. Это уравнение прямой, что подтверждается графиками, рассмотренными нами.
Это уравнение прямой, что подтверждается графиками, рассмотренными нами. . Ну и сам вид графика достаточно простой (график 1):
. Ну и сам вид графика достаточно простой (график 1):

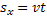 .
.
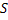 - площадь фигуры, (численно равная пройденному пути), равна полусумме оснований, умноженной на высоту. Обратите внимание, что на рисунке одним из оснований является начальная скорость. А вторым основанием трапеции будет конечная скорость, обозначенная буквой
- площадь фигуры, (численно равная пройденному пути), равна полусумме оснований, умноженной на высоту. Обратите внимание, что на рисунке одним из оснований является начальная скорость. А вторым основанием трапеции будет конечная скорость, обозначенная буквой  , умноженная на
, умноженная на  . Это означает, что высота трапеции
. Это означает, что высота трапеции 
 становится удвоенным. Мы можем записать следующее выражение:
становится удвоенным. Мы можем записать следующее выражение:










 – это перемещение, соединяющее начальную точку движения с конечной.
– это перемещение, соединяющее начальную точку движения с конечной.






















