Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая зависимость между длиной маятника и периодом колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дополнительная часть лабораторной работы заключается в том, чтобы лучше определить взаимосвязь периода колебаний и длины нитяного маятника. Эта зависимость должна определяться математически. Цель дополнительного задания в том, чтобы выявить математическую зависимость между периодом и длиной маятника. Как это можно сделать? Нужно рассмотреть отношение периодов колебаний маятника и отношение длин маятника. Посмотрим на таблицу, которую используем, и обсудим те величины, которые будем туда заносить.
В первой части мы рассмотрим отношение периода из второго опыта, когда длина маятника составляла 20 см. Отношение мы будем искать к периоду, который получили, когда длина маятника составляла 5 см. Отношение самих длин мы рассмотрим в нижней строке. Итак, в верхней строке отношение периодов То, что мы наблюдали, когда отношение периодов в квадрате равно отношению длин маятника. Из этого следует, что период мы можем записать как Другими словами, если мы увеличиваем длину маятника в 4 раза, то период увеличится в 2 раза. Если увеличим длину маятника в 3 раза, то увеличится период в
Тема: Механические колебания и волны. Звук Урок 31. Кинетическая энергия. Потенциальная энергия. Примеры решения задач Ерюткин Евгений Сергеевич Что такое энергия? Тема урока посвящена энергии. Итак, что это такое? Энергия – это универсальная количественная мера, характеризующая движение и взаимодействие тел. Энергия в механике может быть двух видов – потенциальная и кинетическая. Потенциальная энергия тела над Землей Потенциальная энергия – это энергия взаимодействия. Потенциальная энергия тела, поднятого над Землей, определяется массой тела, ускорением свободного падения и расположением тела относительно Земли: m – [кг] h – [м] Энергия измеряется в джоулях (Дж). Потенциальная энергия в общем случае зависит от выбранной системы отсчета. Ведь высоту мы можем отсчитывать не только от поверхности Земли, но и от условно выбранной какой-то точки или какого-либо уровня Задача Полная энергия Когда мы говорим об энергии, нужно помнить, что тело обладает несколькими видами энергий одновременно. Например, если мы рассмотрим летящий на большой высоте самолет, то можно говорить, что самолет обладает и потенциальной энергией, поскольку находится на некоторой высоте относительно Земли, и кинетической, когда он обладает еще и скоростью.
Рис. 2. Самолет обладает кинетической и потенциальной энергией
Если сложить два вида энергии, то мы получим т.н. полную механическую энергию тела. Список дополнительной литературы: А так ли хорошо знакомо вам понятие энергия? // Квант. — 1985. — №4. — С. 35 Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. — М.: Просвещение, 1990. — С. 119-141. Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – C. 309-347.
Кинетическая энергия Кинетическая энергия – энергия движения тела. Она определяет запас энергии тела, которое обладает скоростью. Кинетическая энергия тоже зависит от того, в какой системе отсчета происходит движение тел. Потенциальная энергия упруго деформированного тела Поговорим о потенциальной энергии упруго деформированного тела. Когда мы деформируем тело, т.е. меняем его форму или объем, то этому телу мы сообщаем некоторую энергию. Пример: мы растягиваем пружину или, наоборот, сжимаем, тем самым изменяя расстояние между атомами и молекулами, и создаем запас потенциальной энергии.
Рис. 1. Удлинение пружины под действием грузика
∆х – это изменение длины пружины, изменение длины тела. ∆х = х – х0 В этом случае мы можем говорить о том, что энергия деформированной пружины будет всегда положительной. Тема: Механические колебания и волны. Звук
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.221.124 (0.006 с.) |


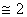


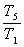
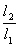 =4
=4



 .
. .
. раз. И т.д. В этом и заключается результат лабораторной работы.
раз. И т.д. В этом и заключается результат лабораторной работы.