
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механические колебания и волныСодержание книги
Поиск на нашем сайте
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
К о л е б а н и я - движения или процессы, обладающие той или иной степенью повторяемости во времени, например: колебания маятника часов, переменный электрический ток, колебания молекул в твердом теле, пульсация излучения звезд и так далее. Во всех колебательных процессах происходит взаимное превращение одного вида энергии в другой, например, в механических колебательных системах кинетическая энергия переходит в потенциальную и обратно, а в электромагнитных - энергия электрического поля переходит в энергию магнитного поля и обратно. Характерной чертой колебательных систем является также наличие устойчивого положения равновесия.
К простейшим периодическим колебаниям относятся г а р м о н и ч е с к и е к о л е б а н и я, в которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер,очень близкий к гармоническим, и, во-вторых,любой периодический процесс можно представить в виде суммы гармонических колебаний. Гармонические колебания. Если в системе совершаются гармонические колебания, то колеблющаяся физическая величина х изменяется со временем по закону
где А- амплитуда колебания, равная наибольшему абсолютному значению отклонения х от положения равновесия;
Выражение (2) для гармонических колебаний можно представить в эквивалентной форме
Если за время t система совершила N колебаний, то время одного колебания - период Различные формы представления гармонических колебаний: а) Метод векторных диаграмм Гармонические колебания можно изобразить графически с помощью вращающегося вектора на плоскости (рис.2). Для этого из начала координат проведем вектор
б) Комплексная форма Пусть Составим комплексное число Z= x+iy,тогда согласно формуле Эйлера
Если ввести комплексную амплитуду
Поэтому гармоническое колебание
Таким образом, можно проводить алгебраические преобразования не с синусами и косинусами,а с экспонентами, что намного проще. Физический же смысл всегда будет иметь только действительная часть конечного выражения, полученного в результате математических операций с комплексными числами.
Гармонический осциллятор Система, совершающая гармонические колебания, называется гармоническим осциллятором.
3.2.1. Пружинный, физический и математический маятники. Рассмотрим в качестве гармонического осциллятора механическую систему с одной степенью свободы, совершающую малые колебания около положения равновесия без трения. Примерами такой системы являются пружинный, физический и математический маятники. П р у ж и н н ы й м а я т н и к - груз массы m, подвешенный на невесомой абсолютно упругой пружине жесткостью k. При подвешивании груза пружина растянется на величину При выведении груза из положения равновесия (т. О на оси х) на тело будет действовать сила со стороны пружины При описании колебаний в механических системах необходимо исходить из основного закона механики(второй закон Ньютона), который для пружинного маятника при отсутствии сил трения имеет вид С учетом (3) и равенства ускорения тела
Вводя обозначение
Это линейное однородное дифференциальное уравнение второго порядка, описывающее гармонические колебания. Решением этого уравнения является функция
где Ф и з и ч е с к и й м а я т н и к - твердое тело, которое может вращаться вокруг неподвижной горизонтальной оси, не проходящей через его центр масс. В отсутствии сил трения в подвесе маятника вращательный момент относительно оси качения (т. О) создает только сила тяжести
где
где При малых
Вводя обозначение
решением которого является
где М а т е м а т и ч е с к и й м а я т н и к - материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести. Математический маятник представляет собой предельный случай физического маятника, вся масса которого сосредоточена в его центре масс, поэтому момент инерции математического маятника
Вынужденные колебания В ы н у ж д е н н ы е к о л е б а н и я в о з н и к а ю т п р и в н е ш н е м п е р и о д и ч е с к о м в о з д е й с т в и и н а к о л е б а т е л ь н у ю с и с т е м у. Общей чертой вынужденных колебаний является то,что спустя некоторое время система полностью «забывает» свое начальное состояние,и в ней устанавливаются незатухающие колебания с частотой внешнего воздействия. Рассмотрим вынужденные колебания на примере механической системы (рис.14). Маятник в виде заряженного шарика на длинном стержне из диэлектрика помещен между вертикальными пластинами плоского конденсатора, на которые подается переменное напряжение. Если внешняя сила
то уравнение движения для маятника имеет вид
Введя обозначения
Решением такого уравнения является сумма общего решения однородного уравнения
где первый член описывает свободные затухающие колебания, второй - незатухающие колебания с частотой Через время, равное времени релаксации
Из этого следует, что
Подставим:
(1) (2) (3) (4) Проведем сложение трех гармонических колебаний в левой части уравнения методом векторных диаграмм. Для этого произвольно расположим вектор
Резонанс Кривая, описывающая зависимость амплитуды вынужденных колебаний от частоты внешнего воздействия W, называется резонансной кривой или амплитудно - частотной характеристикой (АЧХ). П р и п р и б л и ж е н и и ч а с т о т ы в н е ш н е й с и л ы W к ч а с т о т е w0 н а б л ю д а е т с я в о з р а с т а н и е а м п л и т у д ы в ы н у ж д е н н ы х к о л е б а н и й. Э т о я в л е н и е н а з ы в а е т с я р е з о н а н с о м. Рассмотрим физическую сторону этого явления в разных областях частот. Если W<<w0, первый и второй члены в уравнении малы по сравнению с третьим и уравнение движения сводится к виду
В этом случае внешняя сила «идет» на преодоление квазиупругой силы, и колебания будут происходить со статической амплитудой
Если W>>w0, первый член в левой части уравнения много больше остальных и уравнение движения будет иметь вид
Решение его В области резонанса
Таким образом, в условиях резонанса роль внешней силы сводится главным образом к компенсации действующих в механической системе сил трения и ускорение создается силой упругости. При этом система совершает почти «гармонические» колебания с максимальной для нее амплитудой
Значение р е з о н а н с н о й ч а с т о т ы WРЕЗ можно определить из условия минимальности знаменателя в выражении
При d<<w0 , Отсюда следует, что чем выше добротность системы Q, тем острее «резонансный пик» (рис. Поскольку энергия осциллятора пропорциональна квадрату амплитуды, при резонансе система обладает наибольшей энергией ЕРЕЗ. Пусть
Чтобы убедится в справедливости, составим соотношение
Так как то отсюда
ВОЛНЫ Ф р о н т в о л н ы - геометрическое место точек системы, до которых доходят колебания источника к моменту времени t. Фронт волны представляет ту поверхность, которая отделяет часть системы, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
Геометрическое место точек, в которых колебания совершаются в одинаковой фазе, называется в о л н о в о й п о в е р х н о с т ь ю. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости - п л о с к а я в о л н а, или форму сферы - с ф е р и ч е с к а я в о л н а. Волну можно считать сферической на расстояниях значительно превышающих размеры источника (точечный источник) и при условии, что скорость распространения возмущения одинакова по всем направлениям (изотропная среда). Если источник возмущения находится настолько далеко, что волновая поверхность представляет собой плоскость (сфера очень большого радиуса), то говорят о плоской волне. Волна называется п о п е р е ч н о й, если колебания совершаются в направлениях, перпендикулярных к направлению распространения волны. Волна называется п р о д о л ь н о й, если колебания происходят в направлении распространения волны. Волновое уравнение Уравнение для любой волны вида являются решениями дифференциального уравнения, называемого в о л н о в ы м. Установим вид волнового уравнения для плоской волны произвольного вида. Для этого сопоставим вторые частные производные по х и t:
Из соотношений следует
Это дифференциальное уравнение в частных производных второго порядка, которое называется в о л н о в ы м у р а в н е н и е м. Любая функция, удовлетворяющая этому уравнению, будет описывать плоскую волну, распространяющуюся со скоростью V в направлении оси ОХ. Распространение волн в трех измерениях в однородной не поглощающей среде описывается волновым уравнением
или D где D= Для векторной волны волновое уравнение имеет вид D
Волны различной природы Энергия волны При распространении волн происходит перенос энергии без переноса вещества. В силу того, что энергия волны распределена в пространстве неравномерно, имеет смысл говорить о плотности энергии. Упругая среда, в которой распространяются м е х а н и ч е с к и е в о л н ы, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией среды. Рассмотрим плоскую продольную упругую волну в тонком стержне S(x,t)=f(1-x/V). Объемная плотность кинетической энергии определяется следующим равенством:
где dK - кинетическая энергия всех частиц в бесконечно малом объеме dv стержня, выбранном так, что в его пределах скорость частиц среды U(x,t)= Объемная плотность потенциальной энергии
где dП - потенциальная энергия однородно деформированного малого участка среды объемом dV=S0dx; k - малого участка стержня длиной dx и сечением S0, прямо пропорциональная произведению (ES0) и обратно пропорциональная длине этого участка;
Учитывая выражение (99) и равенство
Таким образом, плотности кинетической и потенциальной энергий упругой волны равны между собой в любой момент времени в любой точке среды. Следует отметить, что в отличие от локализованных колебаний осциллятора, где кинетическая и потенциальная энергии изменяются в противофазе (см. (12) и (13)), в бегущей волне колебания кинетической и потенциальной энергий происходят в одинаковой фазе.
Плотность полной энергии упругой волны
Из равенства (114) следует, что энергия бегущей волны перемещается вместе с волной с той же скоростью V без переноса частиц среды, колеблющихся около своих положений равновесия. При этом, согласно закону сохранения энергии, должна уменьшаться энергия источника волн. Для синусоидальной волны (79)
Вектором плотности потока энергии
Скалярная величина I, равная модулю среднего значения вектора Умова, называется и н т е н с и в н о с т ь ю в о л н ы:
Для синусоидальной волны
Интерференция волн. При интерференции наложении волн должны происходить в оном направлении. S2(r,t)=A2sin(w2t-k2r2+j02); определяется выражением где j1-j2=Dj=[(w2t-w1t)-(k2r2-k1r1)+(j02-j01)] - р а з н о с т ь ф а з волн в момент времени t. Для некогерентных волн разность фаз Dj с течением времени меняется, и в этом случае среднее значение квадрата амплитуды <A2> за время много большее периода <A2> = <A12> + <A22> Амплитуда результирующих колебаний будет м а к с и м а л ь н а в тех точках среды, для которых разность фаз равна ч е т н о м у числу p j2-j1=2mp, где m=0,±1,±2,±3,... Если разность начальных фаз j02 - j01=0, то условие м а к с и м у м о в д л я р а з н о с т и х о д а принимает вид или (r2-r1)=ml=2m(l/2) (r2-r1)=(2m+1)(l/2) Стоячие волны Для наблюдения устойчивой интерференционной картины не обязательно иметь два независимых когерентных источника. Вторую, когерентную с исходной, волну можно получить в результате отражения волны от границы среды, в которой происходит распространение волн. В результате и н т е р ф е р е н ц и и п а д а ю щ е й и о т р а ж е н н о й в о л н ы образуется с т о я ч а я в о л н а. Пусть уравнение падающей волны имеет вид S1(x,t)=Acos(w t -kx), тогда уравнение отраженной волны имеет вид S2(x,t)=Acos(w t+kx+j), где j - изменение (сдвиг) фазы волны, возникающее при отражении. При о т р а ж е н и и у п р у г и х в о л н сдвиг фазы зависит от волнового сопротивления Rволн отражающей среды, которое определяется по формуле Rволн=rv, где r - плотность среды, а v - фазовая скорость волны. Пусть волновые сопротивления среды, от которой распространяется волна - r 1v1, а среды, от которой волна отражается - r2v2. При соотношении r1v1< r2v2 волна отражается от более плотной среды и j =p, что соответствует прохождению волной дополнительного расстояния в l/2 (потеря половины длины волны). Если r 1v1>r2 v2, то волна отражается от менее плотной среды и j =0. Учитывая выше сказанное, уравнение отраженной волны можно записать в виде S2(x,t)=± A cos(w t + k x) где «плюс» соответствует j =0,а «минус» j =p. Тогда уравнение стоячей волны получим: S(x,t)=S1(x,t)+S2(x,t)=A[cos(w t-kx)±cos(w t+kx)] =
Точки, в которых амплитуда колебаний в стоячей волне Aст(x)=|2Asin(kx)|, а в стоячей волне Aст(x)=|2Acos(kx)|, достигает максимального значения 2А, называется п у ч н о с т я м и; точки, в которых амплитуда стоячей волны равна нулю, - у з л а м и. Расстояние между узлами равно половине длины бегущей волны. Для стоячей волны на границе всегда узел, для стоячей - пучность (рис.) Стоячая волна по существу уже не является волновым движением, так как в ней отсутствует перенос энергии, потому что падающая и отраженные волны за одно и то же время переносят одинаковую энергию в противоположном направлениях. В упругой стоячей волне максимальные значения кинетической энергии совпадают с пучностями, а максимальные значения потенциальной энергии - с узлами, так как в них происходит наибольшая деформация среды. В электромагнитной стоячей волне энергия электрического поля максимальна в пучностах вектора При наличии отражающих границ с двух сторон условие образования стоячей волны на участке длиной l следующие: l =n , если на границах пучности (рис.)
l =(2n-1) где l - длина бегущей волны, а n = 1, 2, 3.... Частоты, удовлетворяющая условиям, называются с о б с т в е н н ы м и ч а с т о т а м и (гармониками) стоячей волны на данном участке. Условия так же можно представить как условие резонанса, и говорить о наборе р е з о н а н с н ы х ч а с т о т стоячей волны на участке длинной l. спектрального анализа света.
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
К о л е б а н и я - движения или процессы, обладающие той или иной степенью повторяемости во времени, например: колебания маятника часов, переменный электрический ток, колебания молекул в твердом теле, пульсация излучения звезд и так далее. Во всех колебательных процессах происходит взаимное превращение одного вида энергии в другой, например, в механических колебательных системах кинетическая энергия переходит в потенциальную и обратно, а в электромагнитных - энергия электрического поля переходит в энергию магнитного поля и обратно. Характерной чертой колебательных систем является также наличие устойчивого положения равновесия.
К простейшим периодическим колебаниям относятся г а р м о н и ч е с к и е к о л е б а н и я, в которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер,очень близкий к гармоническим, и, во-вторых,любой периодический процесс можно представить в виде суммы гармонических колебаний. Гармонические колебания. Если в системе совершаются гармонические колебания, то колеблющаяся физическая величина х изменяется со временем по закону
где А- амплитуда колебания, равная наибольшему абсолютному значению отклонения х от положения равновесия;
Выражение (2) для гармонических колебаний можно представить в эквивалентной форме
Если за время t система совершила N колебаний, то время одного колебания - период Различные формы представления гармонических колебаний: а) Метод векторных диаграмм Гармонические колебания можно изобразить графически с помощью вращающегося вектора на плоскости (рис.2). Для этого из начала координат проведем вектор б) Комплексная форма Пусть Составим комплексное число Z= x+iy,тогда согласно формуле Эйлера
Если ввести комплексную амплитуду
Поэтому гармоническое колебание
Таким образом, можно проводить алгебраические преобразования не с синусами и косинусами,а с экспонентами, что намного проще. Физический же смысл всегда будет иметь только действительная часть конечного выражения, полученного в результате математических операций с комплексными числами.
Гармонический осциллятор Система, совершающая гармонические колебания, называется гармоническим осциллятором.
3.2.1. Пружинный, физический и математический маятники. Рассмотрим в качестве гармонического осциллятора механическую систему с одной степенью свободы, совершающую малые колебания около положения равновесия без трения. Примерами такой системы являются пружинный, физический и математический маятники. П р у ж и н н ы й м а я т н и к - груз массы m, подвешенный на невесомой абсолютно упругой пружине жесткостью k. При подвешивании груза пружина растянется на величину При выведении груза из положения равновесия (т. О на оси х) на тело будет действовать сила со стороны пружины При описании колебаний в механических системах необходимо исходить из основного закона механики(второй закон Ньютона), который для пружинного маятника при отсутствии сил трения имеет вид С учетом (3) и равенства ускорения тела
Вводя обозначение
Это линейное однородное дифференциальное уравнение второго порядка, описывающее гармонические колебания. Решением этого уравнения является функция
где Ф и з и ч е с к и й м а я т н и к - твердое тело, которое может вращаться вокруг неподвижной горизонтальной оси, не проходящей через его центр масс. В отсутствии сил трения в подвесе маятника вращательный момент относительно оси качения (т. О) создает только сила тяжести
где
где При малых
Вводя обозначение
решением которого является
где М а т е м а т и ч е с к и й м а я т н и к - материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести. Математически
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.187.15 (0.015 с.) |

 , (2)
, (2) - фаза колебания, являющаяся угловой мерой времени, прошедшего от начала колебаний,и определяющая значение х в данный момент времени;
- фаза колебания, являющаяся угловой мерой времени, прошедшего от начала колебаний,и определяющая значение х в данный момент времени; - начальная фаза, равная фазе в момент начала отсчета времени t =0;
- начальная фаза, равная фазе в момент начала отсчета времени t =0; - циклическая частота, имеющая смысл скорости изменения фазы колебания.
- циклическая частота, имеющая смысл скорости изменения фазы колебания.
 .
.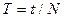 , число колебаний, совершенных за единицу времени - частота
, число колебаний, совершенных за единицу времени - частота  . Циклическая частота
. Циклическая частота  .
. , модуль которого равен амплитуде колебаний А,а сам он повернут относительно оси координат ОХ на угол, равный фазе колебаний
, модуль которого равен амплитуде колебаний А,а сам он повернут относительно оси координат ОХ на угол, равный фазе колебаний  . С течением времени вектор
. С течением времени вектор  , при этом проекции его на оси ОХ и ОУ будут совершать гармонические колебания. Метод векторных диаграмм используется,например,при сложении одинаково направленных гармонических колебаний.
, при этом проекции его на оси ОХ и ОУ будут совершать гармонические колебания. Метод векторных диаграмм используется,например,при сложении одинаково направленных гармонических колебаний. ,а
,а  .
.

 получим:
получим:

 .
. ,то
,то . (2а)
. (2а) , может быть записано как действительная часть комплексного числа Z, обозначаемая ReZ:
, может быть записано как действительная часть комплексного числа Z, обозначаемая ReZ: .
. , определяемую соотношением mg =k
, определяемую соотношением mg =k  ,
,  , по закону Гука.
, по закону Гука. .
. .
. второй производной смещения по времени
второй производной смещения по времени 
 .
. , уравнение движения тела можно записать в виде
, уравнение движения тела можно записать в виде .
. ,
, называется собственной частотой гармонических колебаний пружинного маятника в отсутствии потерь его энергии. Период колебания
называется собственной частотой гармонических колебаний пружинного маятника в отсутствии потерь его энергии. Период колебания  .
. ,
, - расстояние от оси качения до центра масс маятника (т. С),
- расстояние от оси качения до центра масс маятника (т. С),  - угол поворота маятника от положения равновесия. Согласно основному закону динамики вращательного движения
- угол поворота маятника от положения равновесия. Согласно основному закону динамики вращательного движения 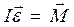 уравнение движения физического маятника имеет вид
уравнение движения физического маятника имеет вид ,
, - момент инерции маятника относительно оси качания, а
- момент инерции маятника относительно оси качания, а  - угловое ускорение, направление которого противоположно направлению момента силы тяжести, о чем говорит знак минус в скалярной записи уравнения движения.
- угловое ускорение, направление которого противоположно направлению момента силы тяжести, о чем говорит знак минус в скалярной записи уравнения движения.
 (радиан). Тогда
(радиан). Тогда .
.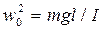 , уравнение движения можно записать в виде
, уравнение движения можно записать в виде ,
, ,
, - амплитуда колебаний угла
- амплитуда колебаний угла  и
и  - собственные частота и период гармонических колебаний физического маятника.
- собственные частота и период гармонических колебаний физического маятника. . Соответственно собственные частота и период гармонических колебаний математического маятника равны
. Соответственно собственные частота и период гармонических колебаний математического маятника равны ,
,  .
. изменяется гармонически с частотой
изменяется гармонически с частотой  и амплитудой
и амплитудой 
 ,
, .
.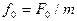 , получим линейное неоднородное дифференциальное уравнение вынужденных колебаний
, получим линейное неоднородное дифференциальное уравнение вынужденных колебаний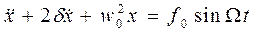 .
. и частного решения неоднородного уравнения
и частного решения неоднородного уравнения ,
, между действием силы и смещением х.
между действием силы и смещением х.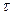 , свободные колебания практически прекращаются и маятник переходит в состояние установившихся вынужденных колебаний с частотой внешней силы
, свободные колебания практически прекращаются и маятник переходит в состояние установившихся вынужденных колебаний с частотой внешней силы  .
. ,
, .
. .
. , описывающий третье колебание. Вектор
, описывающий третье колебание. Вектор  , описывающий первое колебание, опережает его на p, а вектор
, описывающий первое колебание, опережает его на p, а вектор  - на p/2. Так как сумма
- на p/2. Так как сумма  , из рисунка следует
, из рисунка следует ;
; .
. .
. .
. .
. будет описывать колебания с амплитудой
будет описывать колебания с амплитудой  , при которых силы трения и упругости становятся несущественными по сравнению с внешней силой. При W ® ¥ амплитуда колебания А стремится к нулю.
, при которых силы трения и упругости становятся несущественными по сравнению с внешней силой. При W ® ¥ амплитуда колебания А стремится к нулю. первый и третий члены уравнения (51) сравняются, а так как они противоположны по знаку, то
первый и третий члены уравнения (51) сравняются, а так как они противоположны по знаку, то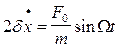 ,
,  .
. .
. ,
, .
. и
и  , а с учетом
, а с учетом 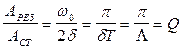 .
. и
и  - циклические частоты, при которых энергия системы убывает в два раза по сравнению с
- циклические частоты, при которых энергия системы убывает в два раза по сравнению с  ,тогда величина
,тогда величина 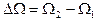 называется шириной резонансной кривой. Для системы с высокой добротностью
называется шириной резонансной кривой. Для системы с высокой добротностью  ;
;  и
и .
. .
. ,а
,а  ,
, ,
, . С учетом можно получить очень важное соотношение между полушириной резонансной кривой
. С учетом можно получить очень важное соотношение между полушириной резонансной кривой 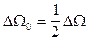 вынужденных колебаний и временем релаксации свободных затухающих колебаний:
вынужденных колебаний и временем релаксации свободных затухающих колебаний: .
.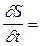
 ;
;  ;
; ;
;  .
.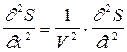 .
.

 ,
,  - оператор Лапласа.
- оператор Лапласа. .
. ,
, одинакова;
одинакова;  - плотность среды.
- плотность среды. ,
, - относительная деформация рассматриваемого участка.
- относительная деформация рассматриваемого участка. ,получим
,получим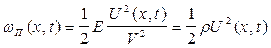 .
. .
.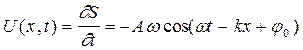 ;
; .
. (вектором Умова) называется вектор, направленный в сторону переноса энергии волны и равный по величине отношению энергии, переносимой волной за единицу времени сквозь малую площадку dS к площади dS^ - проекции этой площадки на плоскость, перпендикулярную направлению переноса энергии. Так как энергия dEмех заключена в элементе объема
(вектором Умова) называется вектор, направленный в сторону переноса энергии волны и равный по величине отношению энергии, переносимой волной за единицу времени сквозь малую площадку dS к площади dS^ - проекции этой площадки на плоскость, перпендикулярную направлению переноса энергии. Так как энергия dEмех заключена в элементе объема , то
, то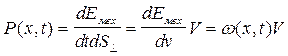 ;
; .
.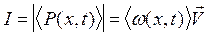 .
. .
.
 (рис.), энергия магнитного поля - в пучностях вектора
(рис.), энергия магнитного поля - в пучностях вектора  .
. , если на границах узлы (рис.)
, если на границах узлы (рис.)


