
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновой пакет. Групповая скорость. Дисперсия.Содержание книги
Поиск на нашем сайте
Плоская синусоидальная волна типа называется м о н о х р о м а т и ч е с к о й и представляет собой бесконечный во времени и в пространстве волновой процесс с постоянной частотой, амплитудой и начальной фазой. Ни одна реальная волна не является строго монохроматической хотя бы потому, что не может длиться бесконечно долго. Но любую волну, используя Фурье разложение (1), можно заменить эквивалентной ей системой синусоидальных волн (спектральное разложение). Совокупность значений амплитуд, начальных фаз и частот такой системы синусоидальных волн называется с п е к т р о м соответственно амплитуд, начальных фаз и частот рассматриваемой синусоидальной волны. Возможность применения спектрального анализа для описания волн основана на действии п р и н ц и п а с у п е р п о з и ц и и, выполнение которого установлено опытным путем. Суть его заключается в следующем: при одновременном распространении волн результирующее смещение частицы среды равно векторной сумме ее смещений, обусловленных каждой из волн в отдельности. Другими словами, волны распространяются независимо друг от друга при условии, что их скорости в данной среде не зависит от интенсивности (линейная среда). Г р у п п о й в о л н или в о л н о в ы м п а к е т о м называют несинусоидальную волну, спектр частот которой характеризуется небольшим разбросом около некоторой основной частоты w0. Простейший волновой пакет представлен двумя плоскими монохроматическими волнами с одинаковыми амплитудами и близкими частотами w1 и w2, распространяющимися вдоль оси ОХ.
где
В этом случае волновой пакет S(x,t) представляет собой плоскую «квазисинусоидальную» волну с частотой w0, волновым числом К0 и амплитудой А
Мгновенный «снимок» такой модулированной по амплитуде волны приведен на рис.. Скорость распространения фронта монохроматической волны есть скорость распространения точек поверхности равной фазы и называется ф а з о в о й с к о р о с т ь ю. За скорость распространения волнового пакета (г р у п п о в а я с к о р о с т ь) принимают скорость перемещения точек, в которой амплитуда волнового пакета имеет какое-либо фиксированное значение. Для волнового пакета групповая скорость по определению равна скорости перемещения точек поверхности равной фазы амплитуды А Dwt-DkХ гр=const, откуда следует Dwdt-DkdХ гр=0. Тогда
Для волнового пакета с непрерывным спектром частот
Групповая скорость равна скорости переноса энергии волновым пакетом. Среда называется н е д и с п е р г и р у ю щ е й,если монохроматические волны с разными частотами распространяются с одной и той же фазовой скоростью
или а зависимость w(k) линейная
В такой среде групповая скорость равна фазовой
и форма волнового пакета не изменяется с течением времени. Среда называется д и с п е р г и р у ю щ е й, если фазовая скорость монохроматических волн одной природы зависит от их частоты
Само же явление зависимости фазовой скорости от частоты называется д и с п е р с и е й. В этом случае зависимость w(k) не является линейной
и форма волнового пакета с течением времени будет изменяться (волновой пакет «расплывается»). Групповая скорость, как характеристика его движения, имеет смысл лишь на тех участках, на которых волновой пакет еще сохраняет свою форму. В этом случае
так как
В зависимости от знака производной
В случае нормальной дисперсии групповая скорость U будет меньше фазовой скорости V гармонической составляющей волнового пакета с доминирующей частотой w0; при аномальной дисперсии групповая скорость U больше фазовой скорости.
Интерференция волн. При интерференции наложении волн должны происходить в оном направлении. S2(r,t)=A2sin(w2t-k2r2+j02); определяется выражением где j1-j2=Dj=[(w2t-w1t)-(k2r2-k1r1)+(j02-j01)] - р а з н о с т ь ф а з волн в момент времени t. Для некогерентных волн разность фаз Dj с течением времени меняется, и в этом случае среднее значение квадрата амплитуды <A2> за время много большее периода <A2> = <A12> + <A22> Амплитуда результирующих колебаний будет м а к с и м а л ь н а в тех точках среды, для которых разность фаз равна ч е т н о м у числу p j2-j1=2mp, где m=0,±1,±2,±3,... Если разность начальных фаз j02 - j01=0, то условие м а к с и м у м о в д л я р а з н о с т и х о д а принимает вид или (r2-r1)=ml=2m(l/2) (r2-r1)=(2m+1)(l/2) Стоячие волны Для наблюдения устойчивой интерференционной картины не обязательно иметь два независимых когерентных источника. Вторую, когерентную с исходной, волну можно получить в результате отражения волны от границы среды, в которой происходит распространение волн. В результате и н т е р ф е р е н ц и и п а д а ю щ е й и о т р а ж е н н о й в о л н ы образуется с т о я ч а я в о л н а. Пусть уравнение падающей волны имеет вид S1(x,t)=Acos(w t -kx), тогда уравнение отраженной волны имеет вид S2(x,t)=Acos(w t+kx+j), где j - изменение (сдвиг) фазы волны, возникающее при отражении. При о т р а ж е н и и у п р у г и х в о л н сдвиг фазы зависит от волнового сопротивления Rволн отражающей среды, которое определяется по формуле Rволн=rv, где r - плотность среды, а v - фазовая скорость волны. Пусть волновые сопротивления среды, от которой распространяется волна - r 1v1, а среды, от которой волна отражается - r2v2. При соотношении r1v1< r2v2 волна отражается от более плотной среды и j =p, что соответствует прохождению волной дополнительного расстояния в l/2 (потеря половины длины волны). Если r 1v1>r2 v2, то волна отражается от менее плотной среды и j =0. Учитывая выше сказанное, уравнение отраженной волны можно записать в виде S2(x,t)=± A cos(w t + k x) где «плюс» соответствует j =0,а «минус» j =p. Тогда уравнение стоячей волны получим: S(x,t)=S1(x,t)+S2(x,t)=A[cos(w t-kx)±cos(w t+kx)] =
Точки, в которых амплитуда колебаний в стоячей волне Aст(x)=|2Asin(kx)|, а в стоячей волне Aст(x)=|2Acos(kx)|, достигает максимального значения 2А, называется п у ч н о с т я м и; точки, в которых амплитуда стоячей волны равна нулю, - у з л а м и. Расстояние между узлами равно половине длины бегущей волны. Для стоячей волны на границе всегда узел, для стоячей - пучность (рис.) Стоячая волна по существу уже не является волновым движением, так как в ней отсутствует перенос энергии, потому что падающая и отраженные волны за одно и то же время переносят одинаковую энергию в противоположном направлениях. В упругой стоячей волне максимальные значения кинетической энергии совпадают с пучностями, а максимальные значения потенциальной энергии - с узлами, так как в них происходит наибольшая деформация среды. В электромагнитной стоячей волне энергия электрического поля максимальна в пучностах вектора При наличии отражающих границ с двух сторон условие образования стоячей волны на участке длиной l следующие: l =n , если на границах пучности (рис.)
l =(2n-1) где l - длина бегущей волны, а n = 1, 2, 3.... Частоты, удовлетворяющая условиям, называются с о б с т в е н н ы м и ч а с т о т а м и (гармониками) стоячей волны на данном участке. Условия так же можно представить как условие резонанса, и говорить о наборе р е з о н а н с н ы х ч а с т о т стоячей волны на участке длинной l. спектрального анализа света.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.255.183 (0.005 с.) |

 ,
, ;
; 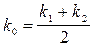 ;
;  ;
;  .
. .
. .
. .
. ,
,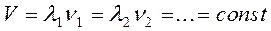 ,
, .
.
 .
.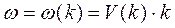
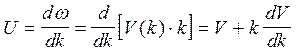 ;
;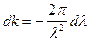 , выражение для групповой скорости можно записать в другом виде
, выражение для групповой скорости можно записать в другом виде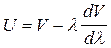 .
. различают н о р м а л ь н у ю д и с п е р с и ю:
различают н о р м а л ь н у ю д и с п е р с и ю: 
 (рис.), энергия магнитного поля - в пучностях вектора
(рис.), энергия магнитного поля - в пучностях вектора  .
. , если на границах узлы (рис.)
, если на границах узлы (рис.)


