
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые характеристики движения по окружностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Угловая скорость обозначается греческой буквой омега (w), она говорит о том, на какой угол поворачивается тело за единицу времени. Это величина дуги в градусной мере, пройденной телом за некоторое время. Заметьте, если твердое тело вращается, то угловая скорость для любых точек на этом теле будет величиной постоянной. Ближе точка располагается к центру вращения или дальше – это не важно, т.е. от радиуса не зависит. Единицей измерения в этом случае будет либо градус в секунду, либо радиан в секунду. Часто слово «радиан» не пишут, а пишут просто с-1. Для примера найдем, чему равна угловая скорость Земли. Земля делает полный поворот на 360° за 24 ч, и в этом случае можно говорить о том, что угловая скорость равна Также обратите внимание на взаимосвязь угловой скорости и линейной скорости: V = w . R. Необходимо отметить, что движение по окружности с постоянной скоростью – это частный случай движения. Однако движение по окружности может быть и неравномерным. Скорость может изменяться не только по направлению и оставаться одинаковой по модулю, но и меняться по своему значению, т.е., кроме изменения направления, существует еще и изменение модуля скорости. В этом случае мы говорим о так называемом ускоренном движении по окружности. Тема: Законы взаимодействия и движения тел Урок 22. Решение задач Ерюткин Евгений Сергеевич
Урок посвящен решению задач Задача 1 Задача 1 посвящена закону всемирного тяготения. Условие: определите высоту, на которой сила тяжести будет в 3 раза меньшей, чем на поверхности Земли. Дано: СИ Решение: R = 6400 км 6400 . 103 м ______________ h -? Ответ: h»4685 км. В условии указано, что сила тяжести должна быть в 3 раза меньше, чем на поверхности Земли. Сила F1 – это сила притяжения тела к Земле на поверхности Земли, а сила F2 на некоторой высоте. Поскольку задача относится к закону всемирного тяготения, давайте этот закон запишем, но сделаем это два раза. Первый раз – для тела, которое находится на поверхности Земли, а второй раз – для тела, которое находится на некоторой высоте относительно поверхности Земли. Итак, F1 – это сила тяготения, или сила притяжения тела, масса, которого m к самой Земле. Сам закон запишется следующим образом: Запишем теперь формулу для силы F2, которая соответствует силе взаимодействия между малым телом m и массой Земли, телом массы Земли на некоторой высоте h: Из условия известно, что F1 и F2 связаны зависимостью: Чтобы сделать следующий шаг, понадобится извлечь квадратный корень из правой и из левой частей. Окончательный ответ получаем в формуле, которая определяет высоту: Если теперь подставить все известные значения, то получим ответ: h»4685 км. Эта задача хорошо показывает возможность определения высоты, на которую можно запустить спутник с таким расчетом, чтобы на него действовала определенного значения сила тяжести. Это является важным условием при исследовании движения спутников. Задача 2 Задача 2 посвящена криволинейному движению. Условие: велосипедист движется по закруглению дороги, радиус закругления дороги 50 м, скорость велосипедиста 36 км/ч. Определите центростремительное ускорение велосипедиста, проходящего закругление дороги, и определите силу трения, которая действует на велосипед. Дано: СИ Решение: R = 50 м V = 36 км/ч 10 м/с FТР = FЦ; FТР = FЦ = m . аЦ; FТР = 60 . 2 =120 H m = 60 кг аЦ -? Ответ: аЦ = 2 м/с2. F -? FТР = 120 H Найти требуется аЦ и силу трения, которая действует на велосипедиста. Для этого в первую очередь 36 км/час переведем в систему СИ – 10 м/с. Обратимся к решению. Вспомните, что центростремительное ускорение определяется как отношение квадрата скорости к радиусу закругления дороги: В этом случае можно записать Вот это и есть центростремительное ускорение. Теперь можем говорить, раз у нас есть центростремительное ускорение, т.е. действует сила, направленная к центру окружности, значит, действует в противовес другая сила – ведь тело движется по окружности постоянного радиуса без проскальзывания и пробуксовки. Это сила трения между колесами и дорогой. В этом случае обязательно мы должны отметить, что FТР=FЦ. По второму закону Ньютона FТР=FЦ=m . аЦ. Итак, FТР =60 . 2 =120 H. Ответ;аЦ = 2 м/с2 и FТР = 120 H. Отметим, что если бы сила трения и центростремительная сила были неравны, то мы бы наблюдали либо проскальзывание, либо пробуксовывание велосипеда по этому закруглению, что нарушило бы его равновесие. Задача 3 Задача 3. Итак, переходим к заключительной, третьей задаче, которая будет посвящена прямолинейному движению. Условие: определите начальную скорость тела, которое, двигаясь вертикально вверх, через 2 с после начала движения достигло скорости 5 м/с. Определите высоту, на которой окажется тело, когда скорость его станет равна 5 м/с. Дано: Решение: t = 2 c V =5 м/с V=V0 – g . t; 5 = V0 – 10 . 2; h -? Ответ: Начнем с начальной скорости. Посмотрите, мы запишем сначала полное уравнение скорости:
Рис. 1. Система отсчета, выбранная для решения задачи
Система отсчета связана с поверхностью Земли. Теперь совместим уравнение, уравнение скорости с выбранной системой отсчета. Обратите внимание, относительно этой системы отсчета начальная скорость Скорость через 2 с, которая определена как 5 м/с, тоже направлена вертикально вверх – Отсюда получаем, что начальная скорость, т.е. скорость, с которой тело бросили вертикально вверх, будет равна Запишем уравнение движения в общем виде: Мы уже сказали, что начальная скорость направлена вертикально вверх, она будет со знаком плюс. Ускорение свободного падения Ответ:
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 721; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.009 с.) |



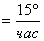 .
.

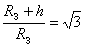






 ;
; 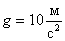 ;
; ;
;  ;
;
 h = 30 м.
h = 30 м.
 направлена вертикально вверх, совпадает по направлению с осью у.
направлена вертикально вверх, совпадает по направлению с осью у. . Ускорение свободного падения
. Ускорение свободного падения  направлено вертикально вниз. Здесь указанной стрелочкой мы обозначили это ускорение. Дальше записываем уравнение: V=V0 – g . t. Подставляя известные значения, имеем: 5 = V0 – 10 . 2.
направлено вертикально вниз. Здесь указанной стрелочкой мы обозначили это ускорение. Дальше записываем уравнение: V=V0 – g . t. Подставляя известные значения, имеем: 5 = V0 – 10 . 2.


