
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема О движении центра масс смтСодержание книги
Поиск на нашем сайте
Введем важное понятие центра масс СМТ введем понятие естественным путем.Рассмотрим выражение для импульса СМТ
Вектор Радиусом вектором центра масс. Иногда называют центром инерции. Очевидно Центр масс-это фиктивная точка которая сосредотачивает в себе всю массу СМТ.положение точки задается ф (2).С учетом опр. Последняя ф. преобразуется следующим образом Ур-е движения для импульса СМТ эквивалентно ур-ю движения МТ вся масса которой сосредоточена в центре. А все внешние силы дейст. На СМТ приложены к ее центру масс. Это утверждение называется теоремой о движении центра масс. Отметим что у СМТ есть еще одно ур-е о движении момента импульса в этом отличие СМТ от МТ. Закон сохранения импульса. Фактически з.с. в механике представляет собой интегралы ур-я движения. СМТ называется изолированной если на нее не действуют внешние силы.Рассмотр. Ур-е движения выведенное на прошлой лекции Ф.(3) и (4) выражают закон сохранения импульса. Для изолир. СМТ импульс системы не изменяется во времени(const)
С учетом этой формулы закон сохр.импульса можно сформулировать:центр масс изолир. СМТ движется равномерно и прямолинейно. Закон сохр. момента импульса. Ранее мы вывели закон импульса всей СМТ
Распишем формулу подробнее:
Формулы (8),(9) и (10) выражают закон сохр.момента импульса для изолир.СМТ:момент импульса не изменяется во времени. Замечание: возможны в механике ситуации, когда
Закон сохранения энергии. 1.изменение: рассмотрим одну матер. Точку. она движется вдоль оси х(см. л №8 и 1) Проведем ряд преобразований в которых лежит второй закон Ньютона.
Следовательно ф(18) перепишется:
если умножить обе части на dt:
(см. л. №8 и. 2) Проинтегрируем (23) от точки 1 до точки 2.
Введем следующую физ.величину А,которая называется работой,
(26) работает когда
!!! Рассматривалось только одномерное движение!!! Закон сохранения энергии в общем случае криволинейного движения м.т. Общий случай движ.м.т. по криволинейной траектории: (см. Л.№8 и.3) В этом случае ур-е имеет вид: вспомним
длина вектора
После сделанных преобразований ур-е (2)
Потенциальные силы. Среди множества видов сил особое место занимают потенциальные силы. (см. Л.№9 и.2)
№21. Потенциальная энергия. Закон сохран. мех. Энергии. По определению потенциал. энерг. мт находящейся под действием потенциал. силы назыв. функция координат такая что элементар. работа Тогда A=
Работа этой силы зависит только от полож. точек в пространстве. Согласно закону измен. кинетич. энергии находящейся под действием потенц. силы:
В силу производности мы можем написать При движ. мт под действ. Только потенц. сил выполняется закон сохранения энергии. Т.е. энергия сохраняется во время движения.
№22. Силы инерции при поступательном ускоренном движении системы отсчета. НСО- система отсчета, движущаяся с ускорением.
Мы знаем что обычная сила изменяет скорость мт (сила как колич.векторная мера взаимодействий между телами), НО к этому приводит и резкое торможение поезда если человек находится внутри. Возникает парадоксальная ситуация, оказывается есть такие системы отсчета, в которых скорость мт может изменяться если на них не действуют силы как мера взаимодействия. Пусть имеется некоторая инерциальная система отсчета которую будем считать не подвижной(ИСО) Пусть XOYZ которая движется ускоренно относительно (ИСО) но поступательно так что оси параллельны Согласно данному выше опред., сист. отсчета XOYZ – будет НСО, мы хотим понять каковы уравнения которые описывают движ. В НСО. Обозначим Для 3 векторов изображ. на (И2) мы видим
Системы поралельны и не меняются во времени. Очевидно
Отметим что в ИСО выполняется 2 з. Ньютона в его обычном виде.
Введенная векторная величина называется силойинерции при поступ. движ. НСО. С точки зрения реальности это сила фиктивна в том смысле что она не относится к мере взаим. тел, и возникает только в НСО когда Это уравнение – есть основ. уравнением динамики мт в НСО, когда последнее движ. поступательно с точки зрения общей теор. относит. не какими экспериментами нельзя различить силы инерции и силы тяготения. На основание этого уравнения можно легко объяснить опыт с поездом.
№23. Общий случай движения НСО: скорость. Равномерное движение точки по окружности См. (И1),(И2) в лекции №11
Описываем изменение во времени
см(И3) в лекции№11
Мы переходим к случаю когда сист. отсчета НСО движется произвольно ИСО. В общем случае это движение можно разложить на 2 состав. Первое это пост. и ускор. движ центра О- этот случай мы рассмотрели ранее. Второе это вращательное движение сист. XOYZ с углов. скор. углов. ускор.
Найдем угловой скоростью
№24. Общий случай движения НСО: ускорение. Продеференцируем обе части
Подставим преобразования:
Вектор Введем вектор
№25.Уравнение динами Мт в НСО.
Применим 2 з. Ньютона для ИСО в S1:
Первое слагаемое в Кореолесова сила определяется с одной стороны вращением НСО, а с другой скоростью Мт относительно S.
№26. Движение Мт относительно вращающейся Земли. Рассмотрим S1 связанная с солнцем приблизительно инерциальна, система S связана с Землей, суточное вращение. Внешнюю реальную силу(результирующую).
Тогда закон механики
По определению вектор
Формулы (1) и (2) совместно являются уравнениями движения Мт.
№27. Вес тела. Маятник Фуко. Весом тела называют силу При этом мы считаем, что тело покоится относительно Земли (НСО). Применим формулу
подставим
С учетом того, что
согласно этой формуле вес тела есть векторная сумма силы гравитационного притяжения Земли Фор-лы (1) и (2) есть конечные формулы вопроса (вес тела). Пусть пл-сть колеб. совпадает с пл-ю рисунка. Маятник имеет скорость
1) 2) 3)
№28.Углы Эйлера. Углы Эйлера -3 угла, которые описывают вращение системы S с тт. относительно S1. Рис.1: Дадим ряд определений: Пл-ть По определению углы Эйлера называются углы: Угол Угол Угол
№29.Вращательное движение. Вращательное движение, при котором 2 его точки остаются всегда неподвижными, прямая проходящая через эти точки - называется осью вращения. Все остальные точки не лежащие на оси описывают окружности в плоскостях оси вращения, центры этих окружностей лежат на оси вращения. Рассмотрим какую либо точку, которая движ. по окружности. R-радиус,
№30.Уровнение движения твердого тела. Мы говорили о том, что тт. есть СМТ мы доказали, что эта система обладает 6 степенями свободы, поэтому для описания СМТ необходимо 6 скалярных уравнений; Эти уравнения есть уравнения описывающие динамику тт. – это 6 скаляр. уравнений Уравнения моментов можно брать относительно произвольного неподвижного начала или относительно центра масс тт.. Можно также брать произвольно движ. начало, если только скорость его в любой момент времени параллельна скорости центра масс. При ограничение свободы движ. число независимых уравнений, требующихся для описания движ. тт., уменьшается. Она всегда равна числу степеней свободы. Внутренние силы не влияют на движ. тт.
(см. и5 лекции 14)
представим, что
( не такая экзотика для полупроводников ) вывод: если между проекциями физ. Величин сущ-ет связь типа (4), причем
Формула (5) уже дает связь между 1) (6)
Формула (8) дает связь проекции
Аналогично получим:
Из 9-ти коэффициентов независимы только 6. Величины осевыми моментами инерции тв. тела. Величины называются центробежными моментами инерции ТТ. Величины называются центробежными моментами инерции ТТ. Векторы
Тензор Величины Тензор
№32.Вычисление моментов инерции относительно оси. Пусть ось Z есть ось вращения.
Момент инерции относительно оси.
Этот предел если существует, то равен объемному интегралу
Формула (5) дает выражение для момента инерции относительно оси в случае непрерывного расположения массы вещества.
(см. рис в лекции №17) Расм. произвольное тв. тело. Пусть точка О –центр масс этого тела, а ось Ri отсчитывается от центра масс. Задача: сравнить осевой момент инерции относительно оси
Ф-ла (2) и (5)
Формула (7) выражает теорему Гюйгенса-Штейнера. №36. Движение тел с переменной массой.
речь не идет о релятивистском изменении массы. Мы называем тело телом с переменной массой если в процессе его движения масса тела меняется за счет потери или приобретения вещества.пример: 3-х ступенчатая ракета. Выгорает топливо, масса уменьшается. Для получения уравнения движения тела с переменной массой нет необходимости привлечения новых физ. Принципов. Это ур-е следует из законов Ньютона .(см. и1 лекции 20) Пусть имеется ракета (см и1) которая имеет массу М(t). Пусть в неподвижной ИСО S скорость ракеты равна dM<0 (2) следовательно мы имеем: dM+dm=0 (3)- закон сохранения массы. Импульс системы в момент времени t:
Для общего случая: Когда действует внешняя сила:
Мы пренебрегаем произведением
Мы учтем силу для общего случая:
Уравнение (9) описывает движение тела с переменной массой в ИСО S при наличии внешних сил F.
Расписываем левую часть (9):
Обозначим через
с учетом (3) перепишем (13)
Формула (15) есть главная формула данного вопроса. Вектор Уравнение (15) называется уравнением Мещерского или уравнением движения тела с переменной массой для общего случая(в присутствии F). №37. Формула Циолковского. (см. и2 в лекции 20)
Спроецируем
Обозначим
Формула (4) называется формулой Циолковского. Эта формула показывает насколько изменится масса ракеты при увеличении скорости от Из этой формулы видно, что для увеличения скорости при минимальном расходе топлива нуж
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

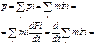
 (1)
(1)
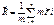
 (2) называется (
(2) называется ( -масса
-масса  частицы.
частицы.  -ее радиус-вектор)
-ее радиус-вектор) (3)-вектор скорости центра масс СМТ.
(3)-вектор скорости центра масс СМТ.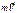
 (4).Импульс всей СМТ=импульсу центра масс. С учетом выведенного закона движения для
(4).Импульс всей СМТ=импульсу центра масс. С учетом выведенного закона движения для 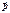 (см.13 вопрос) Эквивалентный вид
(см.13 вопрос) Эквивалентный вид 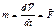 (5)
(5) (1) Очевидно для изолированной СМТ внешние силы =0
(1) Очевидно для изолированной СМТ внешние силы =0  (2) интегрируя Ур-е (2)
(2) интегрируя Ур-е (2) 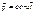 (3)
(3)  (4)
(4) (5)
(5)  -масса всей СМТ.
-масса всей СМТ.  -скорость движения центра масс.
-скорость движения центра масс. (6) М-для изолированных СМТ =0.
(6) М-для изолированных СМТ =0.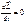 (7) Проинтегрируем Ур-е (7) получим ф(8)
(7) Проинтегрируем Ур-е (7) получим ф(8)  (8)
(8) 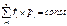 (9)
(9) (10)
(10) , но
, но  спроецируем (6) на оси координат
спроецируем (6) на оси координат  ;
; 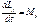 ;
;  (11)
(11)  (12)
(12)  (13)
(13) (14) В таком случае говорят, что система материальных точек описываем. Ур-ем (11) обладает первым интегралом движения (12) или (14).
(14) В таком случае говорят, что система материальных точек описываем. Ур-ем (11) обладает первым интегралом движения (12) или (14).
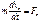 (15)
(15) (16);
(16); 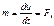 (17);
(17);  (18);
(18);  ;
;  ;
;  ;
; ;
; 
 ;
; 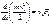 (19)
(19)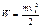 (20) называется кинетической энергией
(20) называется кинетической энергией
 Джоуль (Дж).
Джоуль (Дж). ;
;  ;
;  ;
;  (21)
(21) (22)
(22)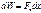 (23)
(23)


 ;
;  (24);
(24);  (25)
(25) сила перемещения м.т. из х1 в х2.
сила перемещения м.т. из х1 в х2. (26) Размерность
(26) Размерность  совпадает. Ф (25) с учетом (26) приобретает окончательный вид.
совпадает. Ф (25) с учетом (26) приобретает окончательный вид.
 (27) выражает закон изменения энергии м.т. для одномерного движения. Изменение кинетической энергии м.т. по перемещ. из 1 в 2 равно работе силы
(27) выражает закон изменения энергии м.т. для одномерного движения. Изменение кинетической энергии м.т. по перемещ. из 1 в 2 равно работе силы 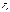 ,действующей на м.т..
,действующей на м.т.. может зависеть от х, но если
может зависеть от х, но если  ,тогда:
,тогда:  если
если  , получаем
, получаем  ;
;  (28)
(28)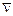 Формула (28) (которая работает при
Формула (28) (которая работает при  ) всегда для одномерного движения называется законом сохранения кинетического движения.
) всегда для одномерного движения называется законом сохранения кинетического движения. (1) на основании закона природы (1) выведем важное отношение для кинетической энергии для общего случая криволинейного движения. Умножим скалярно на
(1) на основании закона природы (1) выведем важное отношение для кинетической энергии для общего случая криволинейного движения. Умножим скалярно на 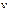 ;
; 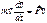 (2)
(2) 
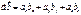

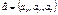 ;
;  ;
;  ;
;
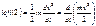
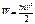 (3)
(3)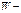 кинетическая энергия (3) м.т. для общего случая криволинейного движения. Размерность
кинетическая энергия (3) м.т. для общего случая криволинейного движения. Размерность  .
. (4)
(4)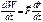 (5) как и для одномерного движения из (5)
(5) как и для одномерного движения из (5)  (6).Проинтегрируем (6) вдоль траектории движения (см.Л.№9 и.1)
(6).Проинтегрируем (6) вдоль траектории движения (см.Л.№9 и.1)  (7)
(7)  (8)
(8)  имеющий направление из 1 в 2.
имеющий направление из 1 в 2.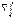 -по контуру
-по контуру  от F как предел следующей суммы:
от F как предел следующей суммы:  (9) где Fi действующая на м.т. на
(9) где Fi действующая на м.т. на 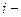 том участке.
том участке. 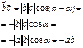
 (см. Л.№9 и.1.2.)
(см. Л.№9 и.1.2.) (10) является следствием интеграла (9).
(10) является следствием интеграла (9).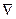 Физ величина
Физ величина  (11) называется работой силы F по перемещению м.т. из 1 в 2 вдоль траектории L.
(11) называется работой силы F по перемещению м.т. из 1 в 2 вдоль траектории L. 
 С учетом определений (7) превращается
С учетом определений (7) превращается  (12) называется законом изменения кин.энергии для общего случая криволинейного движения м.т.
(12) называется законом изменения кин.энергии для общего случая криволинейного движения м.т.  (13)
(13) 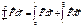 (14) учтем св-во (10) и получим
(14) учтем св-во (10) и получим 
 (15)
(15) по перемещению мт на d
по перемещению мт на d  равна
равна  .
.





 =const
=const Пример про поезд.
Пример про поезд.
 в ИСО.
в ИСО. ---это равенство работает для
---это равенство работает для  .
.
 есть ускорение смт в НСО.
есть ускорение смт в НСО.  является ускорением мт.
является ускорением мт. переносное ускорение- это ускорение начала координат точки О системы НСО относительно ИСО.
переносное ускорение- это ускорение начала координат точки О системы НСО относительно ИСО. 
 представим теперь:
представим теперь: 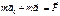 ;
;  ;
; ;
;
 отлична от 0. Ускорение
отлична от 0. Ускорение  которое приобретает Мт будет настолько же реальным на сколько ускорение от реальной силы.
которое приобретает Мт будет настолько же реальным на сколько ускорение от реальной силы.
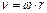 Предадим векторный вид
Предадим векторный вид  Введем радиус вектор мт… и учтем что
Введем радиус вектор мт… и учтем что  направлена по касательной окружности. По построению видно, что
направлена по касательной окружности. По построению видно, что  перпендикулярна плоскости окружности.
перпендикулярна плоскости окружности.

 при условии что его модуль const, а конец движ. со скоростью
при условии что его модуль const, а конец движ. со скоростью  .
.

 с
с ;
;  -единые орты НСО.
-единые орты НСО. Продеференцируем по времени, один раз
Продеференцируем по времени, один раз 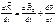
 -это скорость мт в НСО.
-это скорость мт в НСО.  -это скорость в точке О в НСО.
-это скорость в точке О в НСО. с учетом разложения
с учетом разложения  , а так же учитывая то что орты вращаются с
, а так же учитывая то что орты вращаются с .
.
 ;
; 
 ;
;  -скорость мт в НСО,
-скорость мт в НСО,  - скорость нач. координат в НСО,
- скорость нач. координат в НСО,  -скорость Мт в НСО,
-скорость Мт в НСО, 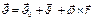 (Общий случай движения НСО: скорость.) по времени
(Общий случай движения НСО: скорость.) по времени
 -ускорение Мт в НСО;
-ускорение Мт в НСО;  -ускорение т. О в НСО;
-ускорение т. О в НСО;
 ;
;  ;
;  ;
; 

 Является окончательной формулой и дает связь между
Является окончательной формулой и дает связь между  и
и  для произвольного движения НСО.
для произвольного движения НСО. - Кориолисово ускорение.
- Кориолисово ускорение. - это вектор назыв. переносным ускорением, именно такое ускор. в НСО имеет Мт, которое покоится.
- это вектор назыв. переносным ускорением, именно такое ускор. в НСО имеет Мт, которое покоится.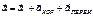 ;
;  ;
;  ;
; ;
;  -настоящая сила.
-настоящая сила. ;
; ; -Это уравнение представляет собой основной закон динамики в НСО, для общего случая поступательного и вращательного ускоренного движения относительно ИСО
; -Это уравнение представляет собой основной закон динамики в НСО, для общего случая поступательного и вращательного ускоренного движения относительно ИСО
 -Кореолесова сила инерции.
-Кореолесова сила инерции. 
 с ускорением поступательного движения системы S. Основные 2 слагаемых возникают из-за,вращательного движения НСО, с угловой скоростью
с ускорением поступательного движения системы S. Основные 2 слагаемых возникают из-за,вращательного движения НСО, с угловой скоростью  .
.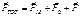 ;
;  -сила притяжения Земли.
-сила притяжения Земли.  -сила притяжения со стороны солнца.
-сила притяжения со стороны солнца. - результирующая всех других сил.
- результирующая всех других сил.
 -ускорения центра Земли под действием гравитации солнца.
-ускорения центра Земли под действием гравитации солнца. ;
;  ;
;
 .
. . (1)
. (1)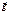 определяемый из равенства
определяемый из равенства  называется вектором свободного падения.
называется вектором свободного падения. (2)
(2) приложенную к телу!!! Которая равна и противоположно направлена силе, с которой подставка действует на тело!
приложенную к телу!!! Которая равна и противоположно направлена силе, с которой подставка действует на тело! ,
,

 ;
;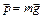 . (1)
. (1) мы видим, что вес тела состоит из 2 частей:
мы видим, что вес тела состоит из 2 частей: (2)
(2) и центробежной силы инерции.
и центробежной силы инерции. ,
,  -начальная к траектории
-начальная к траектории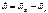

 ;
; -это состав. действ. вдоль нити, растягивающая ее.
-это состав. действ. вдоль нити, растягивающая ее.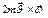 -сила мала и она оказывает малое влияние, т. к.
-сила мала и она оказывает малое влияние, т. к.  .
.
 и
и 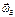 находятся в пл-ти доски. Эта сила
находятся в пл-ти доски. Эта сила 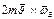 направлена перпендикулярно доске, является частью силы Кориолиса и вызывает смещение пл-ти колебаний, и в результате это смещение становится заметным.
направлена перпендикулярно доске, является частью силы Кориолиса и вызывает смещение пл-ти колебаний, и в результате это смещение становится заметным.
 -прямая по которой пересекаются плоскости
-прямая по которой пересекаются плоскости  и
и 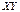 .
. пересекает пл-ть OXY по линии
пересекает пл-ть OXY по линии  (линия узлов), полож. направление совпадает с вектором
(линия узлов), полож. направление совпадает с вектором  .
.  .
.
 является углом собственного вращения.
является углом собственного вращения. называется углом процессии.
называется углом процессии. называется углом нутации.
называется углом нутации. .
.
 ;
;  -угловая скорость вращения тт.
-угловая скорость вращения тт.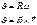
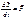 ;
;  ;
; №31.Моменты инерции.
№31.Моменты инерции.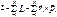
 (1)
(1)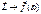
 (2)
(2) (3)
(3)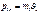
 ,
, (4)
(4) , то видим, что векторы, для которых эта связь справедлива, непараллельны
, то видим, что векторы, для которых эта связь справедлива, непараллельны
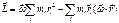 (5)
(5)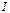 и
и  на оси координат.
на оси координат.  ,
, 
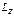
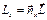
 (
(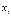 ;
;  ;
; 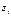 )
)
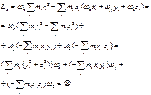
 (7)
(7)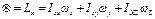 (8)
(8) момента кол-ва движения ТТ и сразу с тремя проекциями вектора угловой скорости
момента кол-ва движения ТТ и сразу с тремя проекциями вектора угловой скорости 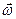
 (9)
(9) (10) Из формул (10) видно:
(10) Из формул (10) видно:  (11)
(11) ,
,  ,
, 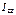 называются
называются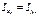 ,
,  ,
, 
 не параллельны. Такая связь, когда связываются 2 не параллельных вектора называется тензорной связью, и говорят, что эта связь определяется с помощью тензора 2-го ранга.
не параллельны. Такая связь, когда связываются 2 не параллельных вектора называется тензорной связью, и говорят, что эта связь определяется с помощью тензора 2-го ранга. (12)
(12) , введенный в формуле (12) с помощью (10) называется тензором инерции твердого тела.
, введенный в формуле (12) с помощью (10) называется тензором инерции твердого тела.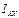 ,
, 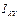 и т.д., называются компонентами тензора.
и т.д., называются компонентами тензора.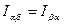 называется симметричным тензором.
называется симметричным тензором.
 (2)
(2) (3)
(3) (4)
(4)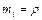 (
(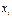 ;
;  ;
; 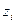 )
) 
 (
( ;
; 
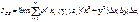


 (5)
(5) проходит через центр масс. Пусть АВ – ось //
проходит через центр масс. Пусть АВ – ось //  и нах-ся на расстоянии а. пусть Ri- радиус i-той точки, лежащей в пл-сти xoy.
и нах-ся на расстоянии а. пусть Ri- радиус i-той точки, лежащей в пл-сти xoy.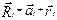 (1)
(1) и оси АВ
и оси АВ от
от 
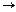 Iо
Iо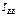 от АВ
от АВ  (2)
(2) (3)
(3) (4)
(4)
 (6)
(6)  (5)
(5)

 (7)
(7)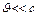 ,
,  км/с
км/с 
 .Пусть в течении малого времени dt происходит выброс массы dm, причем скорость выброса есть u. Мы считаем что система замкнутая, для таких систем выполняется закон сохранения импульса, выполняется закон сохр. массы. Обозначим dM- уменьшение массы ракеты за dt.
.Пусть в течении малого времени dt происходит выброс массы dm, причем скорость выброса есть u. Мы считаем что система замкнутая, для таких систем выполняется закон сохранения импульса, выполняется закон сохр. массы. Обозначим dM- уменьшение массы ракеты за dt.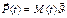 (4)
(4)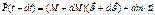 (5)
(5) (6)
(6) (7)
(7)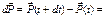
 Получаем:
Получаем: 
 как величину 2-го порядка малости
как величину 2-го порядка малости (8)
(8)
 (9)
(9) - относительная скорость газов относительно ракеты, тогда относительно S
- относительная скорость газов относительно ракеты, тогда относительно S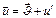 (10)
(10) (11)
(11)
 (12)
(12)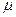 ежесекундный расход топлива
ежесекундный расход топлива (13) {кг/с}
(13) {кг/с}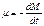 (14)
(14)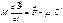 (15)
(15)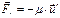 (16) назовем реактивной силой.
(16) назовем реактивной силой.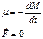 (1)
(1)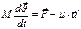 с учетом (1) на ось Z
с учетом (1) на ось Z
 (2)
(2)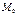 ,
,  - значения массы и скорости перед включением двигателя ракеты
- значения массы и скорости перед включением двигателя ракеты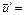 const
const
 (3)
(3) (4)
(4) до
до 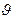 . Из этой формулы можно узнать насколько изменится скорость ракеты.
. Из этой формулы можно узнать насколько изменится скорость ракеты. 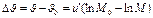 (5)
(5)


