
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
СТО. Интервал и собственное время.Содержание книги
Поиск на нашем сайте
Пусть в точке пространства с координатами x, y, z в момент времени t происходит некоторое физическое явление (событие). Пусть в другой точке x1, y1, z1 в момент времени t, происходит другое событие, тогда по определению интервалом между двумя событиями называется величина равная: S= ▼ Мы показали, что интервал между двумя событиями является инвариантным. Мы рассматриваем бесконечно малые расстояния и интервалы между двумя событиями dx=(x1-x), dt=(t1-t), dS=
55.СТО. 4-х мерная формулировка-преобразование Лоренца и вращение в плоскости x, τ. Математическое отступление. Формулы преобразования координат вектора при повороте в системе (здесь рисунок). Получим связь ax=>f1(ax;ay), ay=> f2(ax;ay), ax= aα=Rαβaβ’ (4), Rαβ= Введем формально четвертую координату. τ=ict (6). Будем считать, что формулы преобразования типа (3) и (4) справедливы и для координатной плоскости τx(здесь рисунок). tgj=i(V/c) (7). Формулы преобразования (3) и (4) в точности совпадают с преобразованиями Лоренца (II). cosj=1/ СТО. 4-х радиус вектор, 4-х векторы скорости и ускорения. По определению четырехрадиусом-вектором называется величина rα=(x, y, z, τ) (10). Мы показали что формула преобразования является следующими формулами: rα=γαβr’β (11). γαβ=(Здесь формула из тетради) (12). Применим (11) к α=1→r1=x, r1=γ11r1’+γ12r2’+γ13r3’+γ14r4’=x’/ Обобщим определение четырехрадиуса-вектора на произвольный трех-вектор. ▼ По определению четырехрадиусом-вектором называется совокупность величин aα=(ax, ay, az, aτ), которые при преобразовании Лоренца (вращение в плоскости xτ на угол j) преобразуется как четырехрадиус-вектор по формуле (11). aα=γαβaβ’ (13) суммирование по индексу β от одного до четырех. Кинематика СТО. dt0 лоренц-скаляр (инвариант), мы это показали. dt0-как масса в обычном мире. ▼ Четырехвектором-скорости называется следующим четырехвектором: uα= ux=dx/(dt
Тривиальная формула преобразования скорости при вращении uα=γαβuβ’ (21) ▼ Четырех-вектор ускорения по определению равен:
uαvα=0 (25) четырех-векторы скорости и ускорения арктагенальны (сколярное произведение=0) 57-58.СТО. Ковариантная формулировка основного закона динамики материальной точки. Сила Минковского. Инерционные свойства частиц описываются массой покоя этой частицы (m0).четырех-вектор импульса. ▼ По определению pα=m0uα (26). Естественным релетивистским обобщением II закона Ньютона является следующее уравнение: ▼ Fα-называется силой Минковского. Запишем в координатах
Тогда уравнение (27) четырех-вектора компоненты приобретают следующий вид: ▼ Справа в (34) стоит мощность, следовательно, слева изменение энергии. ▼ Таким образом мы определяем полную энергию частицы. E= Проанализируем. Формула для трех-координат системы четырех-вектора (трехмерная формула для четырех-вектора): E= E= ▼ (41) дает связь импульса частицы с энергией покоящейся частицы.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.7.116 (0.006 с.) |

 (9). Преобразуем (9), чтобы узнать чему оно равно в системе К’, пользуясь формулами (II). c2(t1-t)2=1/(1-V2/c2){c2(t1’-t’)2+2V(x1’-x’)(t1’-t’)+V2/c2(x1’-x’)2}, (x1-x)2=(x1’-x’)2+V2(t1’-t’)2+2V(x1’-x’)(t1’-t’), (y1-y)2=(y1’-y’)2, (z1-z)2=(z1’-z’)2, c2(t1-t)2-(x1-x)2=1/(1-V2/c2){ c2(t1’-t’)2+2V(x1’-x’)(t1’-t’)+V2/c2(x1’-x’)2-(x1’-x’)2-V2(t1’-t’)-2V(x1’-x’)(t1’-t’)}=1/(1-V2/c2){ (t1’-t’)2(c2-V2)+ (x1’-x’)2(1-V2/c2)}= 1/(1-V2/c2){c2(t1’-t’)2(1-V2/c2)-(x1’-x’)2(1-V2/c2)}=c2(t1’-t’)2-(x1’-x’)2, S2=c2(t1-t)2-(x1-x)2-(y1-y)2-(z1-z)2=c2(t1’-t’)2-(x1’-x’)2-(y1’-y’)2-(z1’-z’)2=S’2 (10). S=S’=invar (11).
(9). Преобразуем (9), чтобы узнать чему оно равно в системе К’, пользуясь формулами (II). c2(t1-t)2=1/(1-V2/c2){c2(t1’-t’)2+2V(x1’-x’)(t1’-t’)+V2/c2(x1’-x’)2}, (x1-x)2=(x1’-x’)2+V2(t1’-t’)2+2V(x1’-x’)(t1’-t’), (y1-y)2=(y1’-y’)2, (z1-z)2=(z1’-z’)2, c2(t1-t)2-(x1-x)2=1/(1-V2/c2){ c2(t1’-t’)2+2V(x1’-x’)(t1’-t’)+V2/c2(x1’-x’)2-(x1’-x’)2-V2(t1’-t’)-2V(x1’-x’)(t1’-t’)}=1/(1-V2/c2){ (t1’-t’)2(c2-V2)+ (x1’-x’)2(1-V2/c2)}= 1/(1-V2/c2){c2(t1’-t’)2(1-V2/c2)-(x1’-x’)2(1-V2/c2)}=c2(t1’-t’)2-(x1’-x’)2, S2=c2(t1-t)2-(x1-x)2-(y1-y)2-(z1-z)2=c2(t1’-t’)2-(x1’-x’)2-(y1’-y’)2-(z1’-z’)2=S’2 (10). S=S’=invar (11).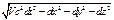 (12). Пусть дана инерциальная система отсчета К’, в некоторой точке x’, y’, z’ происходит два события во время dt0-измеряется часами, покоящимися в К’. Время dt0 есть собственное время, прошедшее между двумя событиями. Найдем интервал между двумя событиями. dS=
(12). Пусть дана инерциальная система отсчета К’, в некоторой точке x’, y’, z’ происходит два события во время dt0-измеряется часами, покоящимися в К’. Время dt0 есть собственное время, прошедшее между двумя событиями. Найдем интервал между двумя событиями. dS=  =cdt0, dt0=
=cdt0, dt0=  (13)-связь интервала и времени. Подставим в (13) dS из формулы (12): dt0=
(13)-связь интервала и времени. Подставим в (13) dS из формулы (12): dt0= 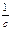


 =(
=( ) (14)
) (14)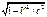 . dt0=dt
. dt0=dt  (15)-связывает собственное время dt0 с временем dt в К’.
(15)-связывает собственное время dt0 с временем dt в К’. +ay
+ay  y (1),
y (1),  +ay’
+ay’ 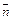 y’ (2)
y’ (2) =
=  +j), ax=ax’cosj-ay’sinj(3)
+j), ax=ax’cosj-ay’sinj(3) (5), a’x
(5), a’x 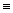 ax’ aα=
ax’ aα=  , a’α=
, a’α=  , ax=Rxxa’x+Rxya’y. Конец матем. отступления.
, ax=Rxxa’x+Rxya’y. Конец матем. отступления. =1/
=1/  (8), sinj=cosjtgj, sinj=(iV/c)/
(8), sinj=cosjtgj, sinj=(iV/c)/  =(1/
=(1/  )(x’-ict’iV/c)=(x’+Vt’)/
)(x’-ict’iV/c)=(x’+Vt’)/  (I). Проверим вторую формулу τ=(x’iV/c+τ’)/
(I). Проверим вторую формулу τ=(x’iV/c+τ’)/  . t=(t’+x’V/c2)/
. t=(t’+x’V/c2)/  . Таким образом поварот системы координатной плоскости xτ на угол j, дает для x, y, z и t формулу Лоренца.
. Таким образом поварот системы координатной плоскости xτ на угол j, дает для x, y, z и t формулу Лоренца. +0+0+(-iV/c)(ict’)/
+0+0+(-iV/c)(ict’)/ 
 (14), dt0=dt
(14), dt0=dt  (15), β=V/c (16), dt0=dt
(15), β=V/c (16), dt0=dt  (17).
(17). )=dx/dt/
)=dx/dt/  =
=  /
/  (18), uy=
(18), uy= 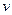 y/
y/  , uz=
, uz=  (20).
(20). =uαuα=-c2, uαuα=1/
=uαuα=-c2, uαuα=1/  (
( +
+ 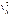 +
+ 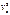 -c2)=
-c2)= 

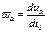 (22), он четырех-вектор по построению. Формула преобразования Лоренца для ускорения:
(22), он четырех-вектор по построению. Формула преобразования Лоренца для ускорения:  γαβvβ’ (23). Компоненты ускорения. vx=
γαβvβ’ (23). Компоненты ускорения. vx=  =
= 
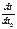 =
= 


 =
=  ; a=vx, b=
; a=vx, b=  ; b’=
; b’= 
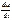



 =-
=- 


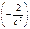
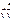
 vx=
vx=  +
+  (24);
(24);  =uαuα=-c2=const; 2ux
=uαuα=-c2=const; 2ux  =0
=0 =Fα (27), Fα-некоторый четырех-вектор.
=Fα (27), Fα-некоторый четырех-вектор.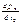 =
= 
 =
= 
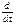
 =Fx.
=Fx.
 =Fx
=Fx  (28); v<<c. Мы потребуем, чтобы в правой части (28) стояла обычная сила F, тогда: ▼ Компоненты четырех-вектора силы:
(28); v<<c. Мы потребуем, чтобы в правой части (28) стояла обычная сила F, тогда: ▼ Компоненты четырех-вектора силы:  =Fx
=Fx 
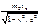 =
=  (30)-обыкновенные силы Ньютона.
(30)-обыкновенные силы Ньютона.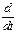
 =Fτ uαvα=0, uα
=Fτ uαvα=0, uα  (m0 uα), воспользуемся (27): uαFα=0 (31).
(m0 uα), воспользуемся (27): uαFα=0 (31).
 +
+ 
 +
+ 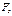
 +
+ 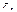
 =0;
=0;  =-
=- 
 ;
;  =(i/c)
=(i/c)  (32);
(32);  =
=  (33)
(33)
 =
= 
 =
=  ;
; 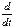
 =
=  (34)
(34) (35);
(35);  =
=  (36)
(36)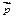 =
= 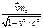 ;
;  m(v)
m(v)  (37); m(v)=
(37); m(v)= 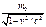 (38);
(38);  =
=  ; pα=(px, py, pz, i, E/c) (39).
; pα=(px, py, pz, i, E/c) (39).

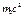 =
=  +…; E=
+…; E= 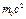 (40) для покоящегося тела. T=E-E0
(40) для покоящегося тела. T=E-E0  [m(0)-m0]c2
[m(0)-m0]c2 ;
;  =
= 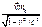 =>
=>  =
=  (41).
(41).


