
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение электронов В магнитном полеСтр 1 из 2Следующая ⇒
ДВИЖЕНИЕ ЭЛЕКТРОНОВ В МАГНИТНОМ ПОЛЕ Цель работы. Определение удельного заряда электрона Приборы и принадлежности: э кспериментальная установка марки «PHYWE» фирмы HYWE Systems GmbH & Co. (Германия) в составе: электронно-лучевая трубка; катушки Гельмгольца (1 пара); источник питания универсальный (2 шт.); цифровой мультиметр (2 шт.); разноцветные соединительные шнуры.
Введение Удельным зарядом элементарной частицы называют отношение заряда частицы к её массе Удельный заряд электрона Многочисленные экспериментальные методы определения удельного заряда частиц
Магнитное поле. Опыты показывают, что магнитное поледействует на движущиеся в нём заряженные частицы.Силовой характеристикой, определяющей подобное его действие, является магнитная индукция – векторная величина В. Магнитное поле изображают с помощью силовых линий магнитной индукции, касательные к которым в каждой точке совпадают с направлением вектора B. При однородном магнитном поле вектор B постоянен по величине и направлению в любой точке поля. Сила, действующая на заряд q, движущийся со скоростью V в магнитном поле, была определена немецким физиком Г. Лоренцем (сила Лоренца). Она выражается формулой
F л = q∙ [ V∙B ] или Fл = | q | VB∙sin α (1)
где α – угол, образованный вектором скорости V движущейся частицы и вектором индукции магнитного поля В.
На неподвижный электрический заряд магнитное поле не действует. В этом его существенное отличие от поля электрического. Направление силы Лоренца определяется с помощью правила «левой руки ». Если ладонь левой руки расположить так, чтобы в неё входил вектор B, а четыре вытянутых пальца направить вдоль направления движения положительных зарядов (q >0), совпадающие с направлением тока I (
покажет направление силы, действующей на положительный заряд (q >0) (рис. 1). В случае отрицательных зарядов (q< 0) направления тока I и скорости V движения противоположны. Направление силы Лоренца определяется по направлению тока. Таким образом, сила Лоренца перпендикулярна вектору скорости, поэтому модуль скорости не будет меняться под действием этой силы. Но при постоянной скорости, как следует из формулы (1), остаётся постоянным и значение силы Лоренца. Из механики известно, что постоянная сила, перпендикулярная скорости, вызывает движение по окружности, то есть является центростремительной. При отсутствии других сил, согласно второму закону Ньютона, она сообщает заряду центростремительное или нормальное ускорение
где α – угол между векторами V и B.
В случае α = 900, sinα = 1 из формулы (2) радиус круговой траектории заряда определяется формулой
Работа, совершаемая над движущейся зарядом в магнитном поле постоянной силой Лоренца, равна Δ А = F л. Δ r или Δ А = F л.Δ r cosβ, (4)
где β – угол между направлением векторов силы F л. и направлением вектора перемещения Δ r.
Период вращения (время одного полного оборота), равен
Рис.2
Подставив в (5) вместо радиуса r его выражение из (3), получим, что кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: период обращения не зависит от энергии частицы, зависит только от индукции магнитного поля и величины, обратной удельному заряду:
Если магнитное поле однородно, но начальная скорость заряженной частицы V направлена под углом α к силовым линиям В, то движение можно представить как суперпозицию двух движений: равномерного прямолинейного в направлении, параллельном магнитному полю со скоростью V // = V∙cosα и равномерного
Рис.3
вращения под действием силы Лоренца в плоскости, перпендикулярной магнитному полю cо скоростью V ┴= V∙sinα. В результате траектория движения частицы будет представлять собой винтовую линию (рис.3). Шаг винтовой линии равен расстоянию, пройденному зарядом вдоль поля со скоростью V // за время, равное периоду вращения h = VТcos, (7) где Подставив это выражение для Т в (7), получим
Ось спирали параллельна силовым линиям магнитного поля B.
Электрическое поле. На точечный заряд q, помещённый в электрическое поле, характеризующееся вектором напряжённости E, действует сила F = q E, (9) Направление силы F совпадает с направлением вектора E, если заряд положительный, и противоположно E в случае отрицательного заряда. В однородном электрическом поле вектор напряжённости в любой точке поля постоянен по величине и направлению. Если движение происходит только вдоль силовых линий однородного электрического поля, оно является равноускоренным прямолинейным. По второму закону Ньютона F = m a уравнение движения заряда в электрическом поле выражается формулой q E = Предположим, что точечный отрицательный заряд, двигающийся первоначально вдоль оси Х со скоростью V, попадает в однородное электрическое поле между пластинами плоского конденсатора, как показано на рис. 4.
Рис. 4
Движение заряда вдоль оси X является равномерным, его кинематическое уравнение x = x 0 + Vt (x 0 – начальная координата, t – время), V = const, x 0 = 0. Время пролёта зарядом конденсатора с длиной пластин ℓ равно Движение вдоль оси Y определяется электрическим полем внутри конденсатора. Если зазор между пластинами мал по сравнению с их длиной, краевыми эффектами можно пренебречь и электрическое поле в пространстве между пластинами считатьоднородным (Еy = const). Движение заряда будет равноускоренным Vy = V 0y + at. У скорение определяется с формулой (10). Выполнив интегрирование (10), получим Траектория и характер движения заряженной частицы в однородном электрическом поле плоского конденсатора подобны аналогичным характеристикам движения в гравитационном поле брошенного горизонтально тела. Отклонение заряженной частицы вдоль оси Y равно
При перемещении заряда в электрическом поле между точками, имеющими разность потенциалов U, электрическим полем совершается работа, вследствие чего заряд приобретает кинетическую энергию. В соответствии с законом сохранения энергии
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряжённостью E, то результирующая сила F, определяющая его движение, равна векторной сумме силы, действующей со стороны электрического поля и силы Лоренца F эм = q E + q [ V∙B ]. (11)
Это выражение называется формулой Лоренца. В данной лабораторной работе исследуется движение электронов в магнитном и электрическом полях. Все соотношения, рассмотренные выше для произвольного заряда, справедливы и для электрона. Считаем, что начальная скорость электрона равняется нулю. Попадая в электрическое поле, заряд ускоряется в нём, и, пройдя разность потенциалов U, приобретает некоторую скорость V. Её можно определить из закона сохранения энергии. В случае нерелятивистских скоростей (V << скорости света c) имеющего вид
где е = –1,6∙10-19Кл – заряд электрона, m e = 9,1∙10-31 кг – его масса. Из (12) скорость электрона
Подставляя её в (3), получим формулу для нахождения радиуса окружности, по которой движется электрон в магнитном поле:
Таким образом, зная разность потенциалов U, ускоряющую электроны при их движении в электрическом поле до нерелятивистских скоростей, индукцию однородного магнитного поля B, в котором эти электроны движутся, описывая круговую траекторию, и, экспериментально определяя радиус указанной круговой траектории r, можно вычислить удельный заряд электрона
Экспериментальная установка
Фото измерительного стенда представлено на рис.5. Рис. 5
Рис.6 На рис. 7 приведены основные узлы экспериментальной установки с обозначениями функциональных частей.
1 − электронно−лучевая трубка; 2, 6 − цифровые мультиметры; 3 – источник питания ИП1 катушек Гельмгольца; 4 − катушки Гельмгольца; 5 − источник питания ИП2 электронно-лучевой трубки.
Рис.8
На рис. 9 показана схема подключения катушек Гельмгольца к источнику питания ИП1.
Рис. 9
При пропускании тока через катушки в пространстве между ними возникает магнитное поле, характеризующееся высокой степенью однородности. Оно является результатом суперпозиции магнитных полей, индуцируемых каждым витком с током кольцевого проводника Индукция магнитного поля в центре кольцевого проводника с током, содержащего один виток, выражается формулой
где R – радиус кривизны проводника, I – сила тока в нём, µ– магнитная проницаемость, µ0 – магнитная постоянная (µ0 = 4π·10-7 Гн/м). Величина индукции магнитного поля на оси катушек пропорциональна току I, протекающему в обмотке каждого из кольцевых проводников и числу витков в них n. Теоретический расчёт магнитной индукции поля катушек Гельмгольца с использованием закона Био–Савара–Лапласа и принципа суперпозиции на оси X в центре системы приводит к адаптированной формуле для расчёта В, используемой в данной работе
где R – радиус кольцевого проводника, µ0 = 4π·10-7 Гн/м (магнитная постоянная).
На рис.10 показано распределение индукции магнитного поля в пространстве между катушками Гельмгольца вдоль оси x, совпадающей с осью симметрии катушек. Пунктиром показаны распределения магнитных полей, создаваемых каждым из кольцевых проводников.
Рис. 10
Неоднородность генерируемого поля при соответствующей юстировке катушек может не превышать 5%.
Электронно-лучевая трубка (ЭЛТ), используемая в экспериментальной установке, показана на рис.11. Фото (вид сверху) иллюстрирует также её месторасположение в пространстве между катушками Гельмгольца в области однородного магнитного поля. ЭЛТ представляет собой лучевой тетрод в стеклянной колбе сферической формы с вакуумом. В колбе расположена электронная пушка - катод косвенного накала, закреплённый на металлической траверсе с перемычками. Для визуализации электронного пучка используется наполнение стеклянной колбы водородом при низком давлении.
Рис.11. Электронно-лучевая трубка с катушками Гельмгольца (вид сверху): 1 – электронная пушка; 2 – траверса с перемычками, используемая как шкала для оценки радиуса траектории электронов; 3 – катушки Гельмгольца.
Испускаемые катодом вследствие термоэлектронной эмиссии электроны фокусируются электродами электронно-лучевой пушки в виде пучка и движутся по прямолинейной траектории вертикально вверх. При подаче на катушки Гельмгольца напряжения от источника питания ИП1 в области размещения ЭЛТ, создаётся однородное магнитное поле. Траектория электронного пучка изменяется из прямолинейной в кольцевую кольцевую.
Рис. 12
Эффект наблюдается визуально по слабому свечению голубоватого цвета внутри стеклянной колбы, соответствующему траектории пучка электронов. Диаметр визуализированной траектории электронов оценивается с помощью расположенной в колбе перекладины с несколькими перемычками, покрытыми люминофором (рис.12).
На рис.13 показана схема подключения к источнику питания ИП2 электронно-лучевой трубки с указанием диапазонов изменения параметров источника.
Рис.13
Рис. 14. Источник питания катушек Гельмгольца (ИП1) (фото передней панели).
Рис. 15. Источник питания электронно– лучевой трубки (ИП2) (фото передней панели). Порядок выполнения работы ПРИМЕЧАНИЕ 1. Все приборы и функциональные элементы установки соединены, соединительными шнурами. НЕ ТРОГАТЬ! ВНИМАНИЕ. При выполнении работы необходимо строго соблюдать правила техники безопасности, установленные на рабочем месте и в лаборатории.
ВНИМАНИЕ.
ВНИМАНИЕ. Измерения необходимо проводить в затемнённом помещении, чтобы наблюдать траекторию пучка электронов. ПРИМЕЧАНИЕ 4. На экспериментальной установке возможно проводить также измерения радиуса траектории пучка электронов с использованием для регистрации третьей слева перемычки шкалы, расположенной в стеклянной колбе ЭЛТ. Она, соответствует радиусу пучка электронов r3 = 0,03 м (рис.12). 14. Эти измерения проводить по требованию преподавателя. Повторить пункты 11 и 12 несколько раз, наблюдая пересечение электронного пучка с третьей перемычкой.
15. Данные измерений соответствующих пар характеристик: ускоряющего напряжения U и тока в катушках I и для каждого опыта при r3 = 0,03 м занести в табл. 2. 16. Выключить измерительную установку. Порядок выключения: а) ручками регулировки уменьшить ток в катушках Гельмгольца до нуля (повернуть в крайнее левое положение). На ИП1 левую и правую ручку установить на 0. б) ручками регулировки уменьшить ускоряющее напряжение электронно-лучевой трубки до нуля (повернуть в крайнее левое положение на ИП2 2– ую и 3– ю ручки). в) выключить источники питания ИП1 и ИП2 (тумблеры на задней панели).
Таблица 1
Таблица 2
Список литературы
1. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Изд-во «Академия», 2005 и далее. – 720 с. 2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2004 и далее. – 544 с. 3. Савельев И.В. Курс общей физики в 3-х тт. – М.: Астрель АСТ, 2007 и далее. Захарова Т.В.(общ. ред.) Физика. Сборник заданий в тестовой форме ч.2. – М.: МИИТ, 2010 – 192 с. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В МАГНИТНОМ ПОЛЕ Цель работы. Определение удельного заряда электрона Приборы и принадлежности: э кспериментальная установка марки «PHYWE» фирмы HYWE Systems GmbH & Co. (Германия) в составе: электронно-лучевая трубка; катушки Гельмгольца (1 пара); источник питания универсальный (2 шт.); цифровой мультиметр (2 шт.); разноцветные соединительные шнуры.
Введение Удельным зарядом элементарной частицы называют отношение заряда частицы к её массе Удельный заряд электрона Многочисленные экспериментальные методы определения удельного заряда частиц
Магнитное поле. Опыты показывают, что магнитное поледействует на движущиеся в нём заряженные частицы.Силовой характеристикой, определяющей подобное его действие, является магнитная индукция – векторная величина В. Магнитное поле изображают с помощью силовых линий магнитной индукции, касательные к которым в каждой точке совпадают с направлением вектора B. При однородном магнитном поле вектор B постоянен по величине и направлению в любой точке поля. Сила, действующая на заряд q, движущийся со скоростью V в магнитном поле, была определена немецким физиком Г. Лоренцем (сила Лоренца). Она выражается формулой F л = q∙ [ V∙B ] или Fл = | q | VB∙sin α (1)
где α – угол, образованный вектором скорости V движущейся частицы и вектором индукции магнитного поля В.
На неподвижный электрический заряд магнитное поле не действует. В этом его существенное отличие от поля электрического. Направление силы Лоренца определяется с помощью правила «левой руки ». Если ладонь левой руки расположить так, чтобы в неё входил вектор B, а четыре вытянутых пальца направить вдоль направления движения положительных зарядов (q >0), совпадающие с направлением тока I (
покажет направление силы, действующей на положительный заряд (q >0) (рис. 1). В случае отрицательных зарядов (q< 0) направления тока I и скорости V движения противоположны. Направление силы Лоренца определяется по направлению тока. Таким образом, сила Лоренца перпендикулярна вектору скорости, поэтому модуль скорости не будет меняться под действием этой силы. Но при постоянной скорости, как следует из формулы (1), остаётся постоянным и значение силы Лоренца. Из механики известно, что постоянная сила, перпендикулярная скорости, вызывает движение по окружности, то есть является центростремительной. При отсутствии других сил, согласно второму закону Ньютона, она сообщает заряду центростремительное или нормальное ускорение
где α – угол между векторами V и B.
В случае α = 900, sinα = 1 из формулы (2) радиус круговой траектории заряда определяется формулой
Работа, совершаемая над движущейся зарядом в магнитном поле постоянной силой Лоренца, равна Δ А = F л. Δ r или Δ А = F л.Δ r cosβ, (4)
где β – угол между направлением векторов силы F л. и направлением вектора перемещения Δ r.
Период вращения (время одного полного оборота), равен
Рис.2
Подставив в (5) вместо радиуса r его выражение из (3), получим, что кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: период обращения не зависит от энергии частицы, зависит только от индукции магнитного поля и величины, обратной удельному заряду:
Если магнитное поле однородно, но начальная скорость заряженной частицы V направлена под углом α к силовым линиям В, то движение можно представить как суперпозицию двух движений: равномерного прямолинейного в направлении, параллельном магнитному полю со скоростью V // = V∙cosα и равномерного
Рис.3
вращения под действием силы Лоренца в плоскости, перпендикулярной магнитному полю cо скоростью V ┴= V∙sinα. В результате траектория движения частицы будет представлять собой винтовую линию (рис.3). Шаг винтовой линии равен расстоянию, пройденному зарядом вдоль поля со скоростью V // за время, равное периоду вращения h = VТcos, (7) где Подставив это выражение для Т в (7), получим
Ось спирали параллельна силовым линиям магнитного поля B.
Электрическое поле. На точечный заряд q, помещённый в электрическое поле, характеризующееся вектором напряжённости E, действует сила F = q E, (9) Направление силы F совпадает с направлением вектора E, если заряд положительный, и противоположно E в случае отрицательного заряда. В однородном электрическом поле вектор напряжённости в любой точке поля постоянен по величине и направлению. Если движение происходит только вдоль силовых линий однородного электрического поля, оно является равноускоренным прямолинейным. По второму закону Ньютона F = m a уравнение движения заряда в электрическом поле выражается формулой q E = Предположим, что точечный отрицательный заряд, двигающийся первоначально вдоль оси Х со скоростью V, попадает в однородное электрическое поле между пластинами плоского конденсатора, как показано на рис. 4.
Рис. 4
Движение заряда вдоль оси X является равномерным, его кинематическое уравнение x = x 0 + Vt (x 0 – начальная координата, t – время), V = const, x 0 = 0. Время пролёта зарядом конденсатора с длиной пластин ℓ равно Движение вдоль оси Y определяется электрическим полем внутри конденсатора. Если зазор между пластинами мал по сравнению с их длиной, краевыми эффектами можно пренебречь и электрическое поле в пространстве между пластинами считатьоднородным (Еy = const). Движение заряда будет равноускоренным Vy = V 0y + at. У скорение определяется с формулой (10). Выполнив интегрирование (10), получим Траектория и характер движения заряженной частицы в однородном электрическом поле плоского конденсатора подобны аналогичным характеристикам движения в гравитационном поле брошенного горизонтально тела. Отклонение заряженной частицы вдоль оси Y равно При перемещении заряда в электрическом поле между точками, имеющими разность потенциалов U, электрическим полем совершается работа, вследствие чего заряд приобретает кинетическую энергию. В соответствии с законом сохранения энергии
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряжённостью E, то результирующая сила F, определяющая его движение, равна векторной сумме силы, действующей со стороны электрического поля и силы Лоренца F эм = q E + q [ V∙B ]. (11)
Это выражение называется формулой Лоренца. В данной лабораторной работе исследуется движение электронов в магнитном и электрическом полях. Все соотношения, рассмотренные выше для произвольного заряда, справедливы и для электрона. Считаем, что начальная скорость электрона равняется нулю. Попадая в электрическое поле, заряд ускоряется в нём, и, пройдя разность потенциалов U, приобретает некоторую скорость V. Её можно определить из закона сохранения энергии. В случае нерелятивистских скоростей (V << скорости света c) имеющего вид
где е = –1,6∙10-19Кл – заряд электрона, m e = 9,1∙10-31 кг – его масса. Из (12) скорость электрона
Подставляя её в (3), получим формулу для нахождения радиуса окружности, по которой движется электрон в магнитном поле:
Таким образом, зная разность потенциалов U, ускоряющую электроны при их движении в электрическом поле до нерелятивистских скоростей, индукцию однородного магнитного поля B, в котором эти электроны движутся, описывая круговую траекторию, и, экспериментально определяя радиус указанной круговой траектории r, можно вычислить удельный заряд электрона
Экспериментальная установка
Фото измерительного стенда представлено на рис.5. Рис. 5
Рис.6 На рис. 7 приведены основные узлы экспериментальной установки с обозначениями функциональных частей.
1 − электронно−лучевая трубка; 2, 6 − цифровые мультиметры; 3 – источник питания ИП1 катушек Гельмгольца; 4 − катушки Гельмгольца; 5 − источник п
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.175.182 (0.208 с.) |
 по известной траектории пучка электронов в электрическом и переменноммагнитном полях.
по известной траектории пучка электронов в электрическом и переменноммагнитном полях. . Эта характеристика широко применяется для идентификации частиц, так как позволяет отличать друг от друга разные частицы, имеющие одинаковые заряды (например, электроны от отрицательно заряженных мюонов, пионов и др.).
. Эта характеристика широко применяется для идентификации частиц, так как позволяет отличать друг от друга разные частицы, имеющие одинаковые заряды (например, электроны от отрицательно заряженных мюонов, пионов и др.). = (1,75896 ± 0,00002)∙1011 Кл∙кг -1.
= (1,75896 ± 0,00002)∙1011 Кл∙кг -1. ), то отогнутый большой палец
), то отогнутый большой палец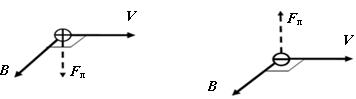 Рис.1
Рис.1 . Траектория движения заряда в однородном магнитном поле при V
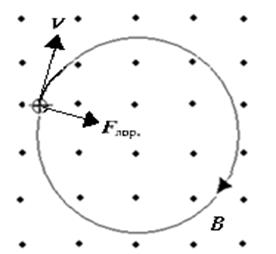
. Траектория движения заряда в однородном магнитном поле при V  B представляет собой окружность (рис.2), радиус которой r определяется из условия
B представляет собой окружность (рис.2), радиус которой r определяется из условия , (2)
, (2) (3)
(3) Так как всегда выполняется условие F л
Так как всегда выполняется условие F л  (5)
(5) . (6)
. (6)
 .
. . (8)
. (8) (10)
(10)
 .
. , где С − постояннаяинтегрирования. При начальном условии (t = 0) V 0y = 0 получим C = 0..
, где С − постояннаяинтегрирования. При начальном условии (t = 0) V 0y = 0 получим C = 0.. . С учётом характера действующей силы оно зависит от
. С учётом характера действующей силы оно зависит от 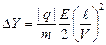 .
. .
. , (12)
, (12) .
.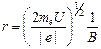 . (13)
. (13) по формуле
по формуле (14)
(14)
 На рис. 6 приведено фото экспериментальной установки марки «PHYWE».
На рис. 6 приведено фото экспериментальной установки марки «PHYWE». Рис.7. Экспериментальная установка:
Рис.7. Экспериментальная установка:






 Функциональные части экспериментальной установки и схемы их подключения
Функциональные части экспериментальной установки и схемы их подключения Катушки Гельмгольца (кольца Гельмгольца) представляют собой два коаксиальных кольцевых проводника одинакового радиуса с n числом витков, расположенные в параллельных плоскостях соосно, таким образом, что расстояние между ними равно радиусу колец (рис.8).
Катушки Гельмгольца (кольца Гельмгольца) представляют собой два коаксиальных кольцевых проводника одинакового радиуса с n числом витков, расположенные в параллельных плоскостях соосно, таким образом, что расстояние между ними равно радиусу колец (рис.8).
 и в целом системы из двух кольцевых проводников (рис.8).
и в целом системы из двух кольцевых проводников (рис.8). ,
,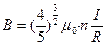 . (15)
. (15)


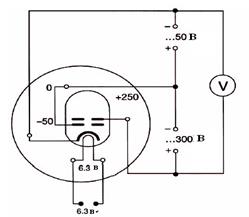


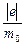 ∙1011, Кл/кг
∙1011, Кл/кг
 )ср. , Кл/кг
)ср. , Кл/кг
 ∙1011 Кл/кг
∙1011 Кл/кг
 )ср. Кл/кг
)ср. Кл/кг
 ∙1011 Кл/кг
∙1011 Кл/кг



