
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон движения ведомого звенаСодержание книги
Поиск на нашем сайте Рассмотрим параболический закон движения. В параболическом законе скорость движения толкателя на первой части фазы удаления равномерно возрастает, а на второй части равномерно убывает до нуля. Ускорение на этих участках остаётся постоянным по величине. Силы инерции изменяют знак в середине подъёма, что приводит к недостаточно спокойной работе механизма из-за возникающей вибрации. Более рациональным будет такое движение толкателя, при котором ускорение постепенно меняет знак, как при подъёме, так и при опускании. Вычисление масштабов:
Рассмотрим построение графика перемещения и графиков первой и второй производной перемещения по углу поворота. График перемещения строится как две сопряжённые ветви параболы, вершина одной находится в начале координат, вершина другой в точке с координатами ( На оси S откладываем максимальный ход ведомого звена Два других графика можно построить аналитическим методом. Амплитудные значения
Аналогично строятся и графики для фазы сближения, амплитудные значения
Определение минимальных размеров кулачкового механизма Переходим к построению графика по оси абсцисс откладываем ординаты первой производной, а по оси ординат – перемещение. Все точки совмещённого графика Для незначительного упрощения построения профиля кулачка выбираем центр для одностороннего вращения кулачка. Соединив центр вращения кулачка т.О1 с началом т.О координат совмещённого графика, получим отрезок О1О, изображающий минимальный радиус кулачка в масштабе
Определение размеров ролика толкателя Для уменьшения износа профиля кулачка и потерь на трение толкатель снабжают роликом. Размер ролика rp выбирают из условия выполнения закона движения(чтобы не получить заострение практического профиля кулачка): rp≤ 0.8ρmin, и из условия конструктивности: rp≤Rmin, где Rmin минимальный радиус кулачка; ρmin – минимальный радиус кривизны профиля кулачка на выпуклой его части. Участки теоретического профиля кулачка с наименьшим ρmin определяют визуально. Затем для этих участков находят центр среднего круга кривизны, проходящего через три ближайшие точки. Средний круг кривизны можно определить и с помощью хорд, соединяющих соседние точки со средней точкой. Через середины каждой из хорд проводят перпендикуляры и находят их пересечение. В точке их пересечения будет находится центр кривизны. Окончательно радиус ролика берётся меньший из двух вычисленных по формулам: rp≤ 0.8ρmin, rp≤ 0.4Rmin Для вычерчивания практического профиля нужно провести ряд окружностей радиусом ролика с центрами на теоретическом профиле, и огибающая этих окружностей будет практическим профилем кулачка. Построение профиля кулачка Построение профиля кулачка можно вести в любом масштабе. Из произвольной точки О1 проводим окружность радиусом Rmin. Через точку О1 проводим луч О1Т, который будет осью толкателя. Пересечение окружности с осью толкателя даёт низшее положение толкателя. На оси движения толкателя от точки нижнего положения О откладываем вверх перемещение толкателя, взятые из графика Совокупность последовательных положений толкателя даёт центровой профиль кулачка. Определяем радиус ролика и строим рабочий профиль кулачка. Замеряем на совмещённом графике
Значение углов давления для каждой фазы движения.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 , [м/мм], где
, [м/мм], где  - максимальное перемещение толкателя на чертеже
- максимальное перемещение толкателя на чертеже , [м/мм], где
, [м/мм], где  - расстояние на чертеже соответствующее фазе удаления
- расстояние на чертеже соответствующее фазе удаления ).
). откладываем фазовый угол удаления
откладываем фазовый угол удаления  восстановим перпендикуляр, на нём отложим hmax=
восстановим перпендикуляр, на нём отложим hmax=  и
и  в масштабе равны:
в масштабе равны: [мм],
[мм],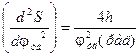 [мм];
[мм]; [мм],
[мм],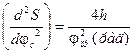 [мм];
[мм]; . Суть построения: исключение аргумента φ из функции
. Суть построения: исключение аргумента φ из функции  и
и  . Каждому углу поворота соответствует ордината S перемещения и ордината первой производной
. Каждому углу поворота соответствует ордината S перемещения и ордината первой производной  . Эти ординаты и являются в дальнейшем координатами совмещённого графика, причём
. Эти ординаты и являются в дальнейшем координатами совмещённого графика, причём соединяем плавной кривой. К полученной кривой проводим справа и слева касательные под углом =300 к вертикальной оси и находим точку О1 их пересечения. Касательные после пересечения ограничивают область, в которой любая точка может быть взята за центр вращения кулачка.
соединяем плавной кривой. К полученной кривой проводим справа и слева касательные под углом =300 к вертикальной оси и находим точку О1 их пересечения. Касательные после пересечения ограничивают область, в которой любая точка может быть взята за центр вращения кулачка. .
.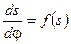 углы передачи движения и давления, которые должны быть
углы передачи движения и давления, которые должны быть  .
.




