
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращательные и поступательное движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В дальнейшем будем рассматривать механическую систему из трех материальных тел, как показано на рис. 18.4. Платформы 2 и 3 совершают лишь вращательные движения (платформа 2 относительно оси
Рис. 18.4
Используя известный «принцип независимости действия сил и моментов» [1], можно при составлении уравнений динамики рассмотреть вращательные движения системы материальных тел и получить связь угловых движений с движущими моментами. Затем, определить дополнительные силы и моменты, вызванные поступательным перемещением начала СК Б4 по дуге окружности радиуса Таким образом, как было показано ранее, при наличии несовпадения точек ЦМ трех тел сложное движение платформы 4 может быть представлено как сумма двух движений: поступательного и вращательного. При изучении вращательного движения платформы 4 вокруг ЦМ
Рис. 18.5
Поступательное пространственное движение соответствует перемещению точки пересечения осей вращения
Все точки тела, движущегося поступательно в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе, поэтому для описания динамики поступательного движения тела достаточно знать динамику движения любой его точки. В рассматриваемом случае движение ЦМ Для учета влияния переносного движения на динамику системы достаточно лишь учесть инерционные силы, обусловленные этим переносным движением, действующие на платформы ОПУ СAС. Если ЦМ Реакции со стороны платформы 4, обусловленные переносным поступательным движением, передаваемые на платформу 3 лежат в плоскости, содержащей ось вращения
Рис. 18.6 Платформа 3 совершает лишь вращательные движения, переносное движение платформы 4 может сказываться на динамике движения платформы 3 лишь через реакции со стороны платформы 4. Если ЦМ платформы 3 лежит на оси
Поскольку ЦМ платформы 4 лежит на оси Таким образом, параллакс по существу (при упомянутых условиях) оказывает влияние лишь на динамику привода В соответствии с выражением для локальной производной:
первые слагаемые системы уравнений Эйлера (18.16) физически представляют собой моменты инерционных сил (например, В отличие от чисто гироскопических тел угловые скорости в выражениях кинетических моментов для рассматриваемого случая не являются постоянными, они изменяются в функции времени, поэтому в общем случае вторые слагаемые уравнений (18.16) характеризуют нелинейные обратные связи гироскопических моментов, вызванных вращениями относительно ортогональных осей.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.52.58 (0.007 с.) |

 , платформа 3 ‒ относительно оси
, платформа 3 ‒ относительно оси  ). Только платформа 4 находится в сложном движении, которое может быть представлено как сумма поступательного движения ЦМ
). Только платформа 4 находится в сложном движении, которое может быть представлено как сумма поступательного движения ЦМ  со скоростью
со скоростью  (оно однозначно связано с изменениями угла поворота
(оно однозначно связано с изменениями угла поворота  ) и вращательного ‒ относительно ЦМ
) и вращательного ‒ относительно ЦМ 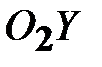 и
и  ). Поскольку вращательное движение платформы 4 должно рассматриваться относительно точки
). Поскольку вращательное движение платформы 4 должно рассматриваться относительно точки  , т.е. с точкой
, т.е. с точкой 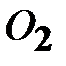 . Таким образом для изучения только вращательного движения рассматриваемой системы материальных тел оси СК Б2, БЗ, Б4, связанные с телами должны иметь общее начало координат, лежащее на оси вращения
. Таким образом для изучения только вращательного движения рассматриваемой системы материальных тел оси СК Б2, БЗ, Б4, связанные с телами должны иметь общее начало координат, лежащее на оси вращения  (точка
(точка 
 относительно оси
относительно оси  в соответствии с изменением
в соответствии с изменением  , и дополнив этими связями математическую модель, составленную с учетом вращательных движений, получить полную математическую модель движения системы трех твердых тел.
, и дополнив этими связями математическую модель, составленную с учетом вращательных движений, получить полную математическую модель движения системы трех твердых тел.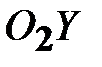 , т.е. система должна рассматриваться так, как будто параллакс
, т.е. система должна рассматриваться так, как будто параллакс  отсутствует (
отсутствует (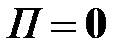 ), как это показано на рис. 18.5.
), как это показано на рис. 18.5.
 и
и  . Это перемещение является плоским поступательным движением относительно оси
. Это перемещение является плоским поступательным движением относительно оси  по окружности с радиусом равным параллаксу
по окружности с радиусом равным параллаксу  .
. платформы 4 в реальной конструкции характеризуется углом поворота
платформы 4 в реальной конструкции характеризуется углом поворота 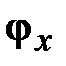 , закон изменения которого полностью определяет динамику плоского поступательного движения платформы 4.
, закон изменения которого полностью определяет динамику плоского поступательного движения платформы 4. с постоянной угловой скоростью
с постоянной угловой скоростью  нормальные силы в опорах платформы 4 пропорциональны центробежным силам, направленным вдоль оси
нормальные силы в опорах платформы 4 пропорциональны центробежным силам, направленным вдоль оси  , при изменениях
, при изменениях  и перпендикулярной к оси вращения
и перпендикулярной к оси вращения  ,и они не создают моментов относительно оси вращения
,и они не создают моментов относительно оси вращения 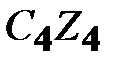 (рис. 18.6).
(рис. 18.6).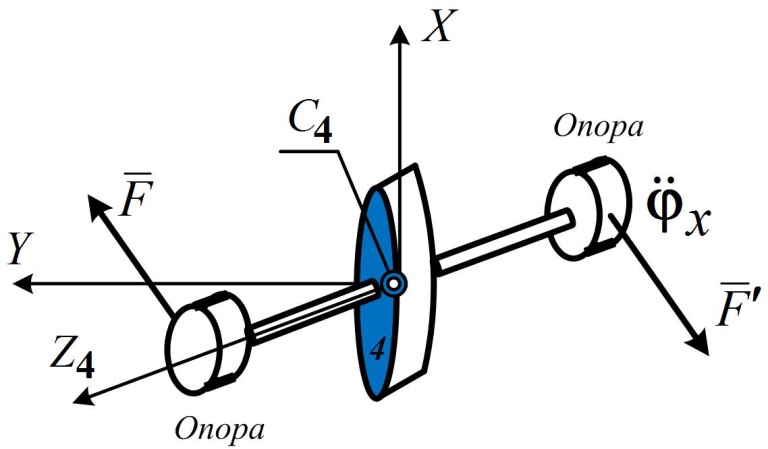
 .
. и то, в виде простого увеличения момента инерции от платформы 4, вызванного ее смещением на величину П относительно оси вращения
и то, в виде простого увеличения момента инерции от платформы 4, вызванного ее смещением на величину П относительно оси вращения  .
.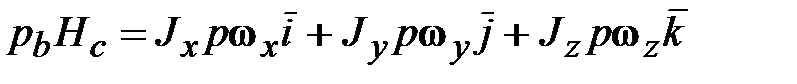
 ‒ это проекция углового ускорения тела в инерциальном пространстве на ось
‒ это проекция углового ускорения тела в инерциальном пространстве на ось  ), вторые слагаемые уравнений (18.16), содержащие произведения угловых скоростей, физически представляют собой гироскопические моменты, обусловленные кинетическими моментами
), вторые слагаемые уравнений (18.16), содержащие произведения угловых скоростей, физически представляют собой гироскопические моменты, обусловленные кинетическими моментами  ,
,  ,
,  и вращениями твердого тела относительно осей, ортогональных к направлениям этих кинетических моментов.
и вращениями твердого тела относительно осей, ортогональных к направлениям этих кинетических моментов.


