
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Часть II анализ динамики пространственного углового сопровождения цели с подвижного авиационного объектаСодержание книги
Поиск на нашем сайте
Часть II АНАЛИЗ ДИНАМИКИ ПРОСТРАНСТВЕННОГО УГЛОВОГО СОПРОВОЖДЕНИЯ ЦЕЛИ С ПОДВИЖНОГО АВИАЦИОННОГО ОБЪЕКТА Раздел 16 ПРИМЕР СЛОЖНОЙ ТЕХНИЧЕСКОЙ СИСТЕМЫ СОПРВОЖДЕНИЯ ПОДВИЖНОГО ОБЪЕКТА БОРТОВОЙ ОПТИЧЕСКОЙ УСТАНОВКОЙ
Авиационный комплекс с бортовым оптическим прибором сопровождения подвижного объекта
Структурные схемы АК БОП в режиме сопровождения (САС) Контур управления слежением СУ ОСП В терминах теории автоматического управления основная задача АК БОП может быть сформулирована следующим образом. Ось чувствительности (оптическая ось ‒ ОО) БОП вращается за счет измерения углового рассогласования между направлениями на подвижный объект (линия визирования ‒ ЛВ) и ОО (визирная ось ‒ ВО – нулевое положение пеленгатора в пространстве). Для реализации управляемого вращения ОО полностью весь корпус БОП или отклоняющие элементы в его оптической схеме размещаются в качестве полезной нагрузки ОПУ, установленной на борту КК и вращаются с помощью приводов по каждой из двух (трех) ортогональных осей. Следовательно, структура СУ ОСП соответствует объединению одноконтурных СП, как показано на рис. 16.6. Структурная схема рассматриваемой локальной СУ включает традиционный набор функциональных элементов: дискриминатор ‒ регулятор ‒ исполнительный орган – объект управления. На рис. 16.6 приняты следующие обозначения: ДиК ОПУ – динамика и кинематика сложного пространственного механического движения карданова подвеса; ИО – исполнительный орган;
Рис. 16.6
Раздел 17 ОСОБЕННОСТИ ЗАДАЧИ ПРОСТРАНСТВЕННОГО УГЛОВОГО СОПРОВОЖДЕНИЯ ЦЕЛИ С ПОДВИЖНОГО ОБЪЕКТА
Трехстепенное опорно-поворотное устройство АК БОП
Параметры поворотов вокруг осей вращения трехстепенного ОПУ
Раздел 18 УРАВНЕНИЯ ДВИЖЕНИЯ ИНЕРЦИОННЫХ МАСС ОПУ САС ПРИ НЕСОВПАДЕНИИ ОСЕЙ ВРАЩЕНИЯ И ЦЕНТРОВ МАСС РАМ ПОДВЕСА ОПУ 18.1 Векторно-матричные методы преобразования СК
Обозначения векторов В дальнейшем будем использовать следующую систему обозначений векторов и матриц. Вектор, существующий в пространстве независимо от выбора СК, называется физическим вектором, а три числа (трехмерное пространство), являющихся составляющими физического вектора и образующих матрицу-столбец (3×1) ‒ математическим вектором:
С математической точки зрения Угловая скорость СК b относительно СК а (абсолютная или инерционная СК) представляется физическим вектором угловой скорости с нижним индексом Производную по времени будем обозначать оператором р. Тогда Символ р без нижнего индекса, предшествующий математическому вектору или матрице, означает дифференцирование по времени каждого элемента вектора или матрицы:
Так как векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
то для представления в матричной форме операции векторного произведения запишем:
Как известно [1], матрица A направляющих косинусов (3×3) преобразует составляющие вектора из одной СК в другую СК:
Дифференцируя уравнение (18.2), получим:
где Запишем, например, с помощью физических векторов известное уравнение Кориолиса [4]:
т.е. изменение Поскольку уравнения (18.3) и (18.4) описывают одну и ту же геометрическую ситуацию, то
что приводит к математической формулировке уравнения Кориолиса:
Умножив обе части уравнения (18.5) на матрицу направляющих косинусов
Момент количества движения
Движение свободного твердого тела в пространстве описывается дифференциальными уравнениями Эйлера в векторной форме [4] с учетом ограничений, описываемых также дифференциальными уравнениям. По смыслу рассматриваемой задачи (вращения вокруг осей, не имеющих поступательного движения в пространстве) покажем дифференциальные уравнения только вращательного движения. Как известно [3], движения ЦМ С твердого тела в инерциальном пространстве описывается выражением (второй закон Ньютона):
Рис. 18.2
где в соответствии с рис. 18.2: ‒ ‒ ‒ ‒ Умножим векторно обе части уравнения (18.9) на вектор
=
После умножения на вектор
где Уравнение (18.10) является математическим выражением второго закона Ньютона для вращения относительно начала отсчета инерциальной (абсолютной) СК. По теореме Кориолиса
а для твердого тела верно
или с учетом формулы для двойного векторного произведения
Отсюда следует, что вектор кинетического момента Запишем для векторов в абсолютной СК
Используя формулу для векторного произведения
где
Так как тензор
Следовательно, угловая скорость и кинетический момент инерции твердого тела совпадают по направлению, когда тело вращается вокруг главной оси инерции.
Вывод уравнения Эйлера Запишем физический вектор кинетического момента инерции в подвижной СК b (
Сумма первых трех слагаемых в (18.13) называется относительной или локальной производной Изменение во времени ортов Так как из определения орта следует Продифференцируем
Рис. 18.3
Аналогично можно записать: Следовательно:
Таким образом, производная по времени от вектора кинетического момента твердого тела в связанной с ним СК b будет определяться уравнением:
Записав векторное уравнение (18.14) в проекциях на оси СК b, связанной с твердым телом (
= ‒ + где Для вращения тела вокруг главной оси инерции последнее выражение упрощается, и уравнения Эйлера в проекциях на оси координат принимают вид:
 ; ;
Если возникает необходимость рассмотрения поступательного движения ЦМ С, то такое движение описывается векторным уравнением (18.9) при условии что равнодействующая всех сил Уравнения Эйлера для поступательного движения в проекциях на оси координат принимают вид:
 ; ;
Векторное уравнение (18.10) и три скалярных уравнения (18.16) описывают вращательное движение ЦМ С в абсолютной (инерциальной) СК; векторное уравнение (18.9) и три скалярных уравнения (18.17) описывают поступательное движение ЦМ твердого тела. При этом, как было принято ранее, оси координат Другими словами движение тела в пространстве представляется в виде двух составляющих: поступательное перемещение начала отсчета подвижной СК Если вращение происходит относительно тоски С, неподвижной в абсолютной СК ( Таким образом, при применении уравнений динамики в форме Эйлера целесообразно сложное движение тела представлять в виде суммы двух движений ‒ переносного поступательного и относительного вращательного.
Часть II АНАЛИЗ ДИНАМИКИ ПРОСТРАНСТВЕННОГО УГЛОВОГО СОПРОВОЖДЕНИЯ ЦЕЛИ С ПОДВИЖНОГО АВИАЦИОННОГО ОБЪЕКТА Раздел 16 ПРИМЕР СЛОЖНОЙ ТЕХНИЧЕСКОЙ СИСТЕМЫ СОПРВОЖДЕНИЯ ПОДВИЖНОГО ОБЪЕКТА БОРТОВОЙ ОПТИЧЕСКОЙ УСТАНОВКОЙ
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.01 с.) |

 ,
,  – пространственные углы ЛВ и ВО в абсолютной системе координат (СК);
– пространственные углы ЛВ и ВО в абсолютной системе координат (СК);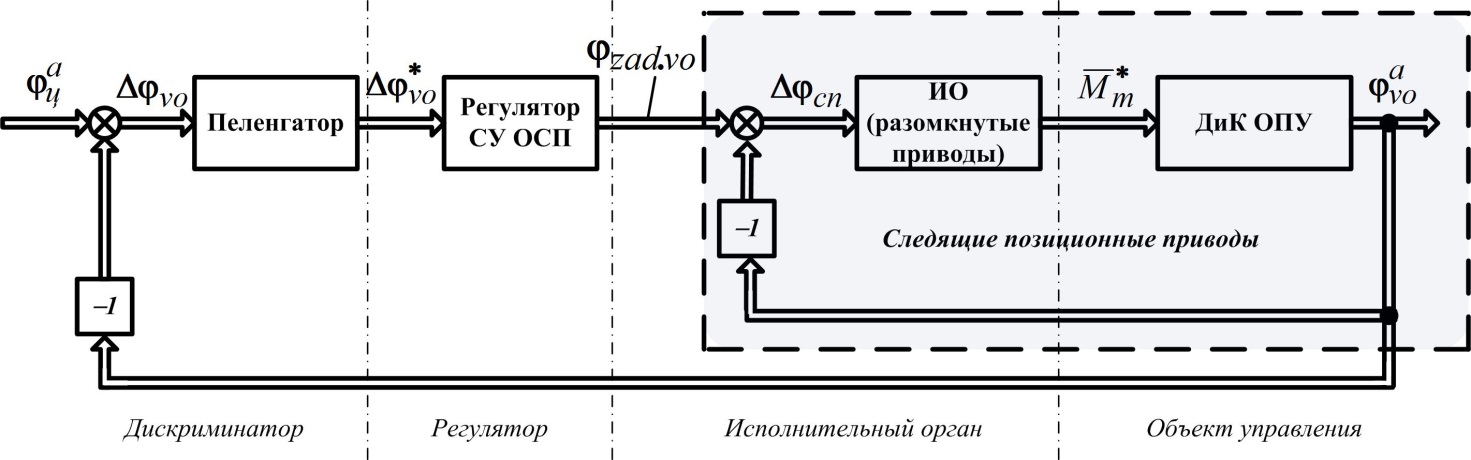
 ,
,  – угловое рассогласование между ЛВ и ВО в пространстве и его измеренное значение;
– угловое рассогласование между ЛВ и ВО в пространстве и его измеренное значение; – выходной сигнал регулятора САС (заданное значение пространственного угла при использовании СП);
– выходной сигнал регулятора САС (заданное значение пространственного угла при использовании СП); – ошибка отработки
– ошибка отработки  ;
; – вектор механических моментов, создаваемых приводами и приложенных к осям вращения ОПУ.
– вектор механических моментов, создаваемых приводами и приложенных к осям вращения ОПУ.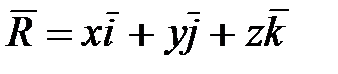 ,
, 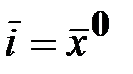 ,
,  ,
, 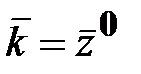 ‒ физический вектор;
‒ физический вектор;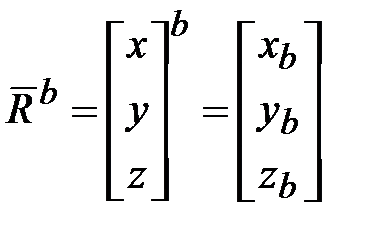 ,
, 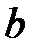 обозначение СК ‒ математический вектор.
обозначение СК ‒ математический вектор. и
и  являются разными величинами, хотя оба этих выражения являются условными представлениями одного и того же физического понятия – положения точки в пространстве.
являются разными величинами, хотя оба этих выражения являются условными представлениями одного и того же физического понятия – положения точки в пространстве.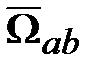 (
(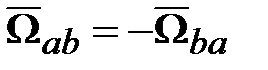 ). Тогда
). Тогда 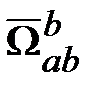 ‒ математический вектор, формируемый составляющими вектора
‒ математический вектор, формируемый составляющими вектора 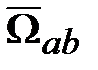 в СК b.
в СК b.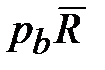 ‒ это скорость изменения физического вектора
‒ это скорость изменения физического вектора 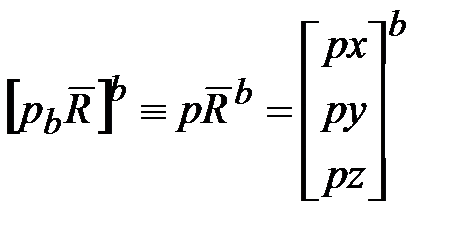 .
.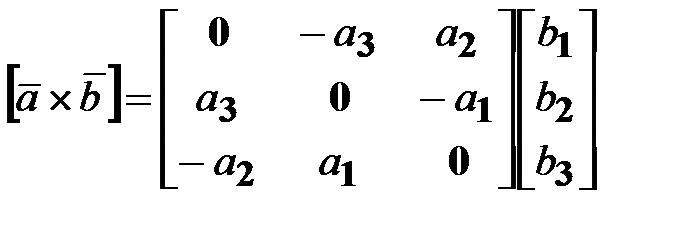 ,
,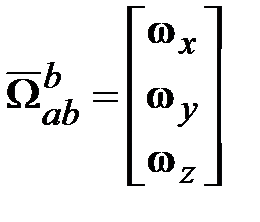 ,
, 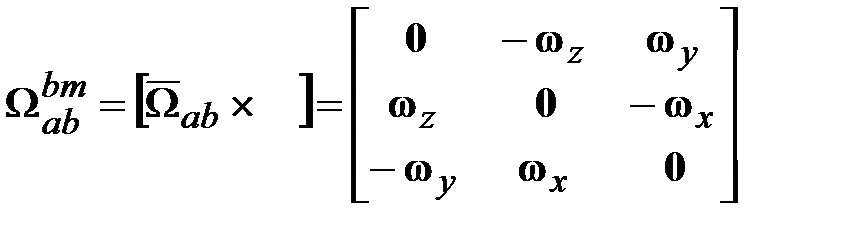 . (18.1)
. (18.1)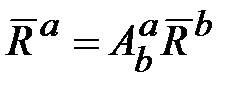 . (18.2)
. (18.2)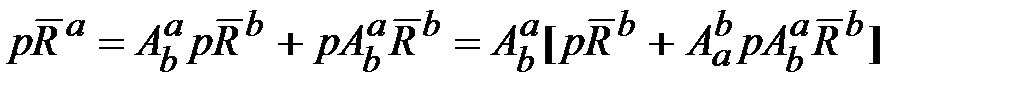 , (18.3)
, (18.3)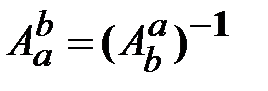 ‒ матрица, обратная
‒ матрица, обратная 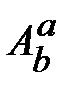 .
.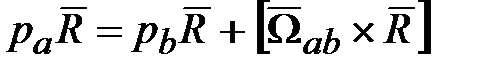 , (18.4)
, (18.4)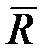 в СК а равно изменению
в СК а равно изменению 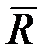 в СК b плюс влияние на
в СК b плюс влияние на 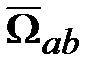 двух СК.
двух СК.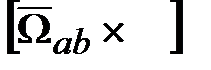 и
и 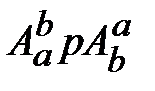 должны быть эквивалентны. Тогда из уравнения (18.1) следует
должны быть эквивалентны. Тогда из уравнения (18.1) следует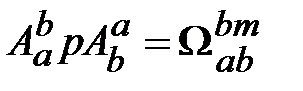 , (18.5)
, (18.5)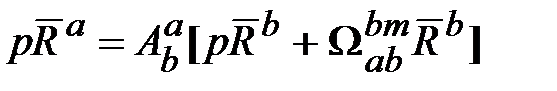 . (18.6)
. (18.6)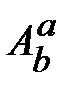 , получим соотношение, описывающее скорость изменения этих косинусов:
, получим соотношение, описывающее скорость изменения этих косинусов: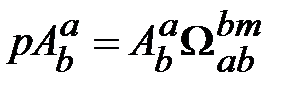 . (18.7)
. (18.7)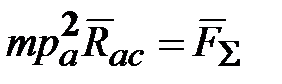 , (18.9)
, (18.9)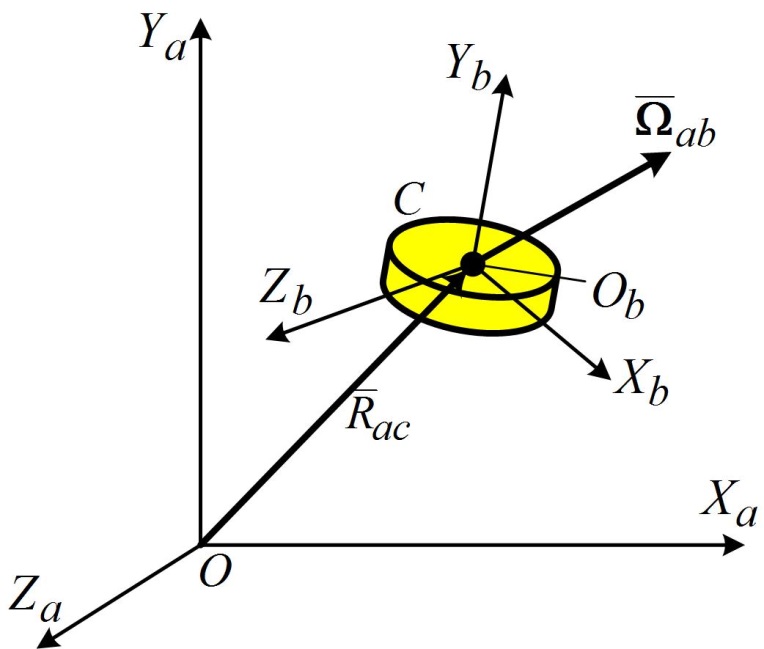
 ‒ радиус-вектор ЦМ С твердого тела с началом в точке
‒ радиус-вектор ЦМ С твердого тела с началом в точке  ;
;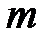 и
и 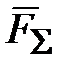 ‒ масса тела и вектор суммы сил, действующих на него;
‒ масса тела и вектор суммы сил, действующих на него;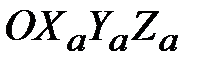 ‒ абсолютная (инерциальная) СК;
‒ абсолютная (инерциальная) СК;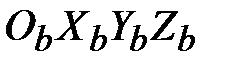 ‒ СК, связанная с телом.
‒ СК, связанная с телом.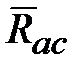 и отдельно преобразуем его левую часть (с учетом
и отдельно преобразуем его левую часть (с учетом 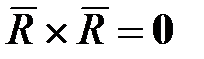 ):
):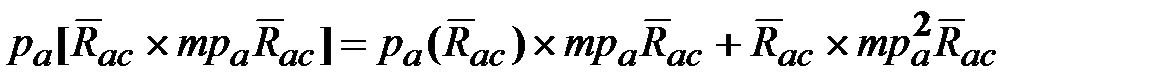 =
=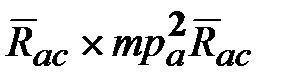 .
.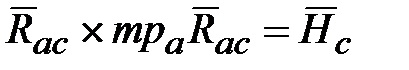 называется кинетическим моментом твердого тела с массой
называется кинетическим моментом твердого тела с массой 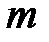 , сосредоточенной в ЦМ С.
, сосредоточенной в ЦМ С.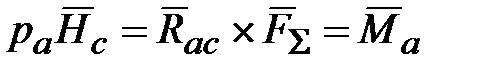 , (18.10)
, (18.10)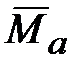 ‒ вектор суммарного момента сил, действующих на твердое тело относительно точки
‒ вектор суммарного момента сил, действующих на твердое тело относительно точки 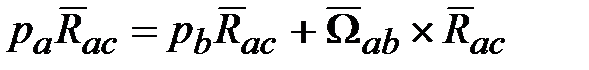 ,
,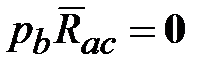 (вращение тела вокруг точки
(вращение тела вокруг точки 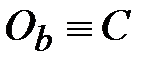 не изменяет вектор
не изменяет вектор 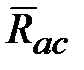 ), т.е. кинетический момент (момент количества движения) можно представить:
), т.е. кинетический момент (момент количества движения) можно представить: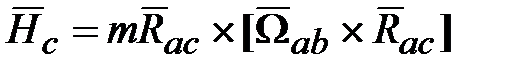 ,
,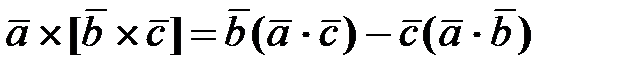 :
: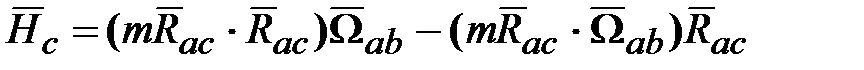 .
.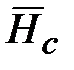 и вектор угловой скорости
и вектор угловой скорости 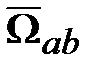 в общем случае не совпадают по направлению.
в общем случае не совпадают по направлению.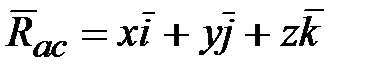 ;
; 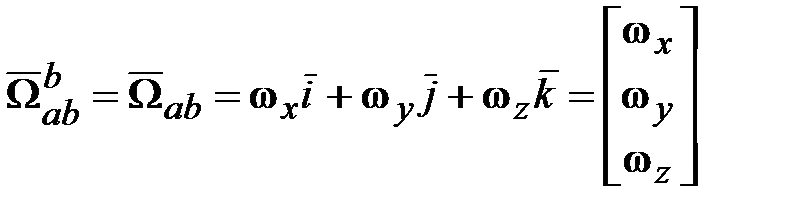 .
.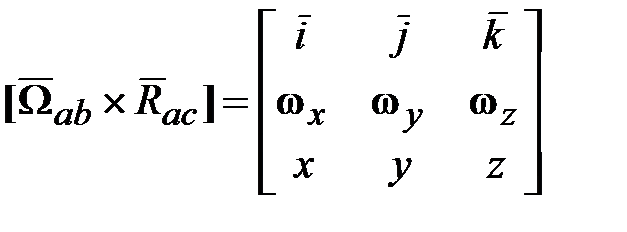 , а также записи
, а также записи 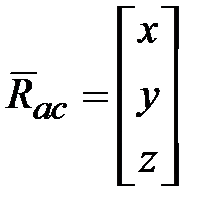 и
и 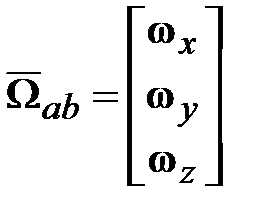 , получим выражение для кинетического момента
, получим выражение для кинетического момента 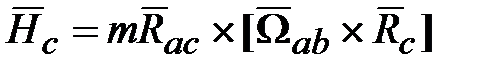 следующим образом.
следующим образом.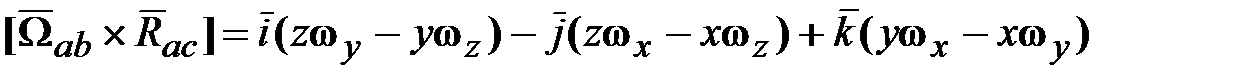 .
.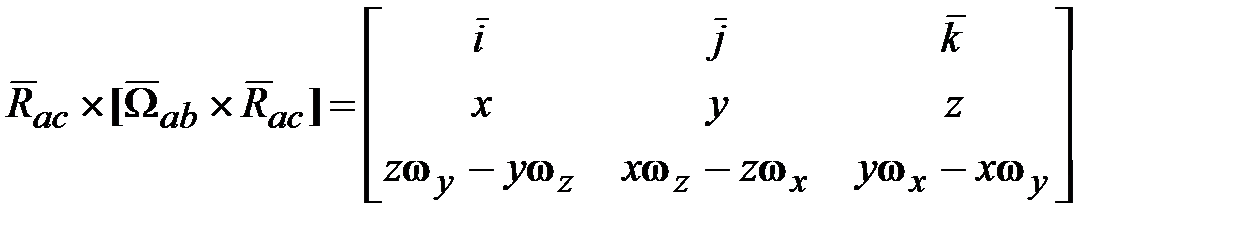
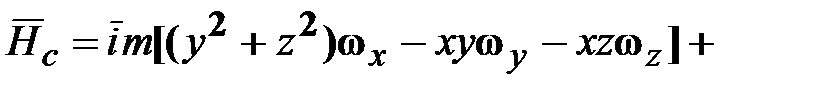
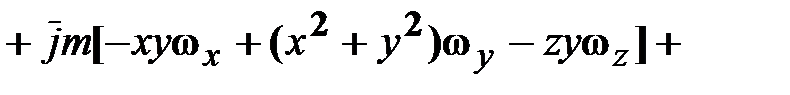
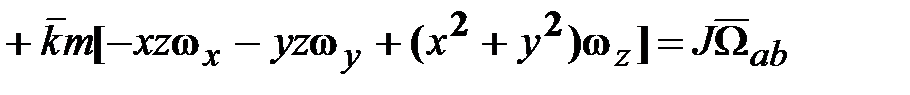 , (18.11)
, (18.11)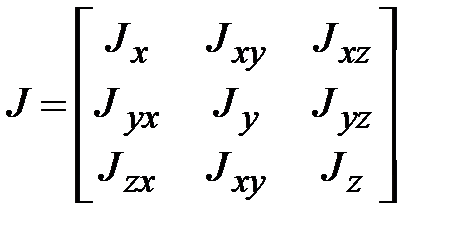 ‒ тензор инерции с элементами
‒ тензор инерции с элементами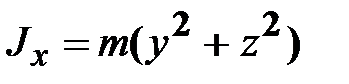 ;
; 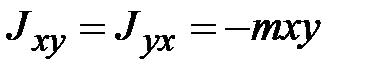 ;
;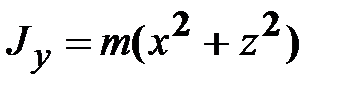 ;
; 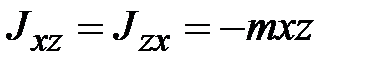
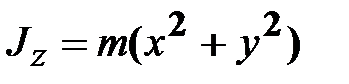 ;
; 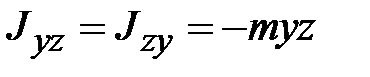 ;
;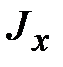 ,
, 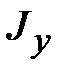 и
и 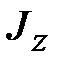 ‒ моменты инерции относительно осей x, y и z, соответственно;
‒ моменты инерции относительно осей x, y и z, соответственно;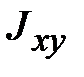 ,
, 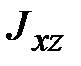 и
и 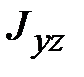 ‒ центробежные моменты инерции.
‒ центробежные моменты инерции. является вещественной, симметричной матрицей, то существует преобразование поворота, приводящее эту матрицу к диагональному виду, т.е. обращающее в нуль все центробежные моменты инерции. Соответствующая СК называется системой главных осей инерции тела. В этом случае выражение (18.11) принимает вид:
является вещественной, симметричной матрицей, то существует преобразование поворота, приводящее эту матрицу к диагональному виду, т.е. обращающее в нуль все центробежные моменты инерции. Соответствующая СК называется системой главных осей инерции тела. В этом случае выражение (18.11) принимает вид: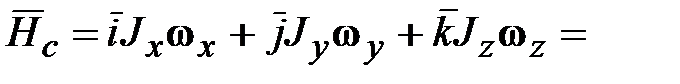
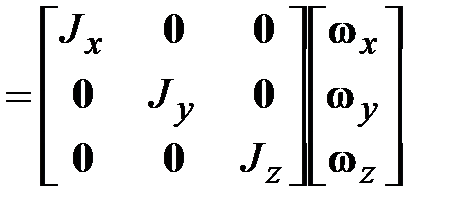 . (18.12)
. (18.12) ):
):  и продифферецируем это выражение в СК
и продифферецируем это выражение в СК  . (18.13)
. (18.13) [4].
[4]. ,
,  и
и 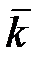 может быть обусловлено только вращением подвижной СК b с угловой скоростью
может быть обусловлено только вращением подвижной СК b с угловой скоростью  , как это показано на рис. 18.3.
, как это показано на рис. 18.3. , то модуль элементарного изменения этого орта при вращении
, то модуль элементарного изменения этого орта при вращении  , где
, где  ‒ угол между вектором мгновенной угловой скорости
‒ угол между вектором мгновенной угловой скорости  и осью
и осью  ;
;  ‒ элементарный угол поворота вокруг вектора мгновенной угловой скорости
‒ элементарный угол поворота вокруг вектора мгновенной угловой скорости  .
.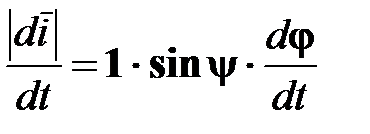 , что с учетом формулы для векторного произведения соответствует записи в векторном виде:
, что с учетом формулы для векторного произведения соответствует записи в векторном виде:  .
.
 и
и  .
.
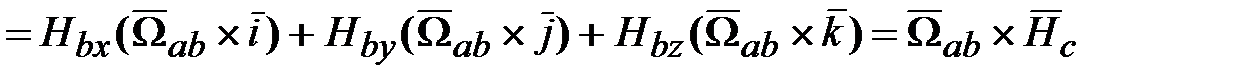 .
. . (18.14)
. (18.14)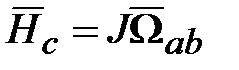 ), получим уравнения движения в форме Эйлера:
), получим уравнения движения в форме Эйлера: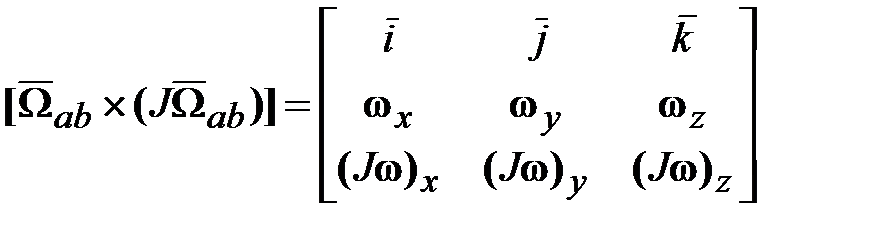 =
= ‒
‒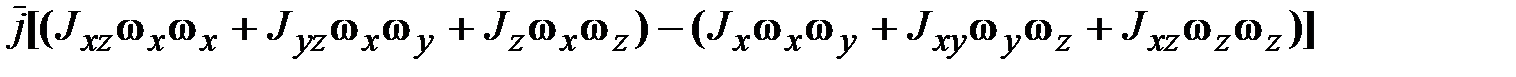 +
+ , (18.15).
, (18.15). .
. ;
; .
. ;
; .
. ,
, 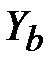 ,
,  , связанные с твердым телом, являются главными центральными осями инерции тела, а моменты инерции
, связанные с твердым телом, являются главными центральными осями инерции тела, а моменты инерции  ,
,  и
и  являются главными центральными моментами инерции.
являются главными центральными моментами инерции. и изменение ориентации (вращение) подвижной СК
и изменение ориентации (вращение) подвижной СК 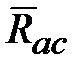 , связывающего два начала отсчета (
, связывающего два начала отсчета ( и
и  ), а вращение ‒ изменением мгновенного вектора угловой скорости
), а вращение ‒ изменением мгновенного вектора угловой скорости  .
. ), то сведений, заключенных в уравнениях (18.10) или (18.16) достаточно для решения задач динамики вращательного движения тела. Если же вращение происходит относительно перемещающейся в абсолютной СК точки С, то к действующим вращательным моментам добавляются силы инерции переносного движения.
), то сведений, заключенных в уравнениях (18.10) или (18.16) достаточно для решения задач динамики вращательного движения тела. Если же вращение происходит относительно перемещающейся в абсолютной СК точки С, то к действующим вращательным моментам добавляются силы инерции переносного движения.


