
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 18 уравнения движения инерционных масс опу сас при несовпадении осей вращения и центров масс рам подвеса опу
18.1 Векторно-матричные методы преобразования СК
Обозначения векторов В дальнейшем будем использовать следующую систему обозначений векторов и матриц. Вектор, существующий в пространстве независимо от выбора СК, называется физическим вектором, а три числа (трехмерное пространство), являющихся составляющими физического вектора и образующих матрицу-столбец (3×1) ‒ математическим вектором:
С математической точки зрения Угловая скорость СК b относительно СК а (абсолютная или инерционная СК) представляется физическим вектором угловой скорости с нижним индексом Производную по времени будем обозначать оператором р. Тогда Символ р без нижнего индекса, предшествующий математическому вектору или матрице, означает дифференцирование по времени каждого элемента вектора или матрицы:
Так как векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
то для представления в матричной форме операции векторного произведения запишем:
Как известно [1], матрица A направляющих косинусов (3×3) преобразует составляющие вектора из одной СК в другую СК:
Дифференцируя уравнение (18.2), получим:
где Запишем, например, с помощью физических векторов известное уравнение Кориолиса [4]:
т.е. изменение Поскольку уравнения (18.3) и (18.4) описывают одну и ту же геометрическую ситуацию, то
что приводит к математической формулировке уравнения Кориолиса:
Умножив обе части уравнения (18.5) на матрицу направляющих косинусов
Момент количества движения
Движение свободного твердого тела в пространстве описывается дифференциальными уравнениями Эйлера в векторной форме [4] с учетом ограничений, описываемых также дифференциальными уравнениям. По смыслу рассматриваемой задачи (вращения вокруг осей, не имеющих поступательного движения в пространстве) покажем дифференциальные уравнения только вращательного движения. Как известно [3], движения ЦМ С твердого тела в инерциальном пространстве описывается выражением (второй закон Ньютона):
Рис. 18.2
где в соответствии с рис. 18.2: ‒ ‒ ‒ ‒ Умножим векторно обе части уравнения (18.9) на вектор
=
После умножения на вектор
где Уравнение (18.10) является математическим выражением второго закона Ньютона для вращения относительно начала отсчета инерциальной (абсолютной) СК. По теореме Кориолиса
а для твердого тела верно
или с учетом формулы для двойного векторного произведения
Отсюда следует, что вектор кинетического момента Запишем для векторов в абсолютной СК
Используя формулу для векторного произведения
где
Так как тензор
Следовательно, угловая скорость и кинетический момент инерции твердого тела совпадают по направлению, когда тело вращается вокруг главной оси инерции.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.137.164 (0.014 с.) |
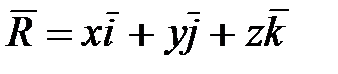 ,
, 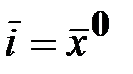 ,
,  ,
, 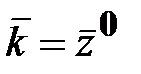 ‒ физический вектор;
‒ физический вектор;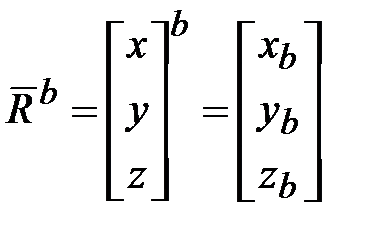 ,
, 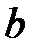 обозначение СК ‒ математический вектор.
обозначение СК ‒ математический вектор. и
и  являются разными величинами, хотя оба этих выражения являются условными представлениями одного и того же физического понятия – положения точки в пространстве.
являются разными величинами, хотя оба этих выражения являются условными представлениями одного и того же физического понятия – положения точки в пространстве.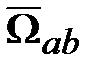 (
(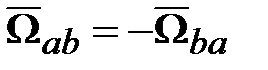 ). Тогда
). Тогда 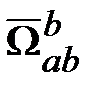 ‒ математический вектор, формируемый составляющими вектора
‒ математический вектор, формируемый составляющими вектора 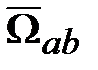 в СК b.
в СК b.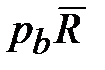 ‒ это скорость изменения физического вектора
‒ это скорость изменения физического вектора 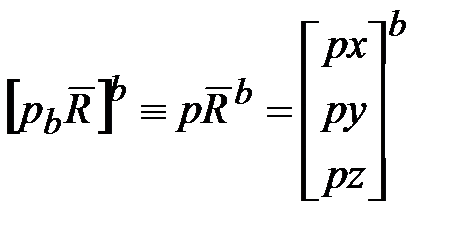 .
.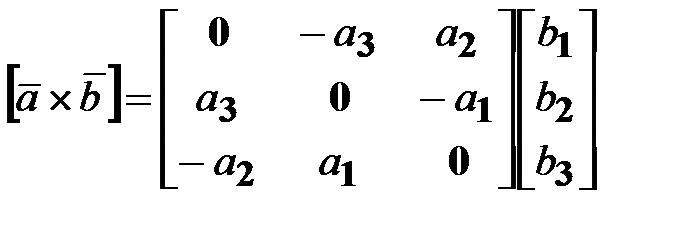 ,
,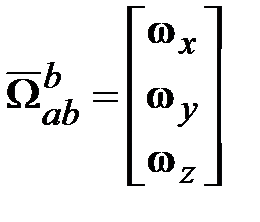 ,
, 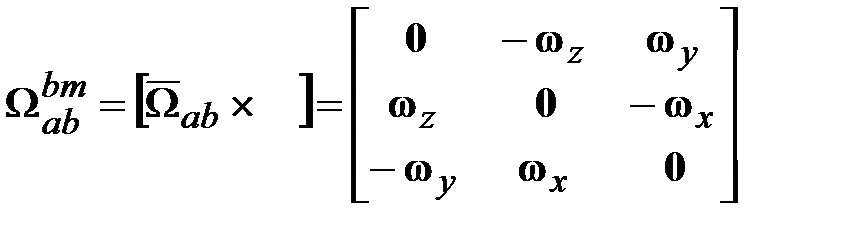 . (18.1)
. (18.1)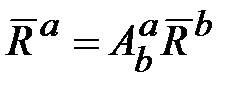 . (18.2)
. (18.2)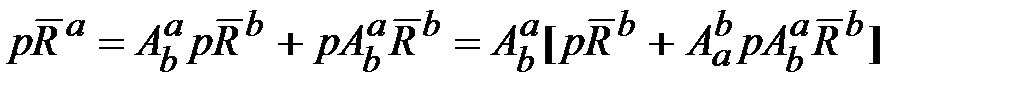 , (18.3)
, (18.3)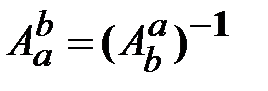 ‒ матрица, обратная
‒ матрица, обратная 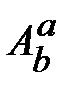 .
.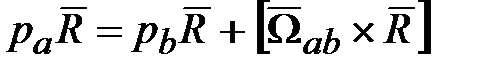 , (18.4)
, (18.4)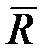 в СК а равно изменению
в СК а равно изменению 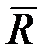 в СК b плюс влияние на
в СК b плюс влияние на 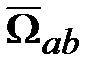 двух СК.
двух СК.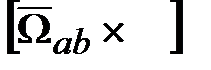 и
и 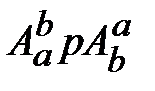 должны быть эквивалентны. Тогда из уравнения (18.1) следует
должны быть эквивалентны. Тогда из уравнения (18.1) следует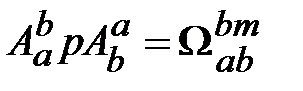 , (18.5)
, (18.5)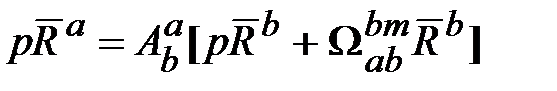 . (18.6)
. (18.6)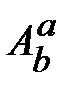 , получим соотношение, описывающее скорость изменения этих косинусов:
, получим соотношение, описывающее скорость изменения этих косинусов: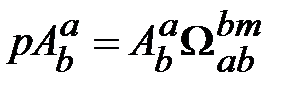 . (18.7)
. (18.7)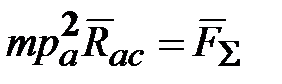 , (18.9)
, (18.9)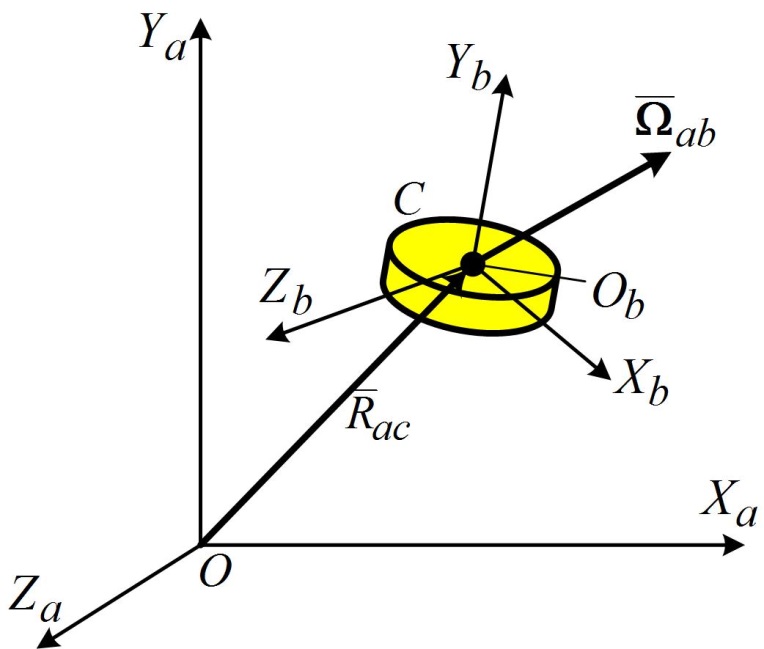
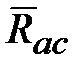 ‒ радиус-вектор ЦМ С твердого тела с началом в точке
‒ радиус-вектор ЦМ С твердого тела с началом в точке  ;
;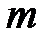 и
и 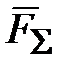 ‒ масса тела и вектор суммы сил, действующих на него;
‒ масса тела и вектор суммы сил, действующих на него;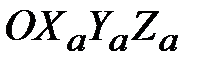 ‒ абсолютная (инерциальная) СК;
‒ абсолютная (инерциальная) СК;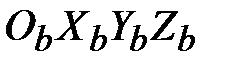 ‒ СК, связанная с телом.
‒ СК, связанная с телом.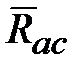 и отдельно преобразуем его левую часть (с учетом
и отдельно преобразуем его левую часть (с учетом 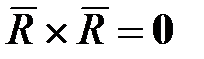 ):
):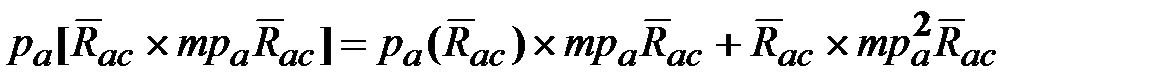 =
=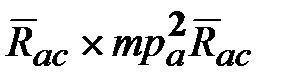 .
.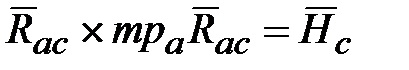 называется кинетическим моментом твердого тела с массой
называется кинетическим моментом твердого тела с массой 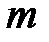 , сосредоточенной в ЦМ С.
, сосредоточенной в ЦМ С.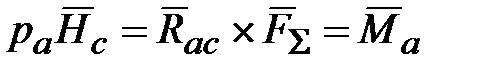 , (18.10)
, (18.10)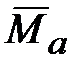 ‒ вектор суммарного момента сил, действующих на твердое тело относительно точки
‒ вектор суммарного момента сил, действующих на твердое тело относительно точки 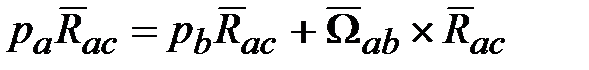 ,
,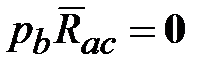 (вращение тела вокруг точки
(вращение тела вокруг точки 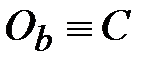 не изменяет вектор
не изменяет вектор 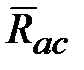 ), т.е. кинетический момент (момент количества движения) можно представить:
), т.е. кинетический момент (момент количества движения) можно представить: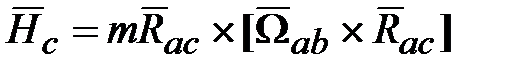 ,
,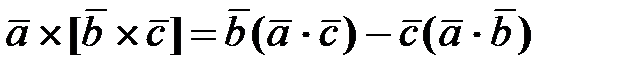 :
: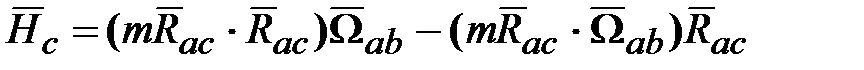 .
.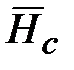 и вектор угловой скорости
и вектор угловой скорости 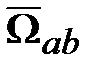 в общем случае не совпадают по направлению.
в общем случае не совпадают по направлению.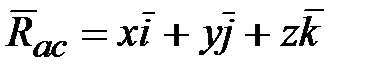 ;
; 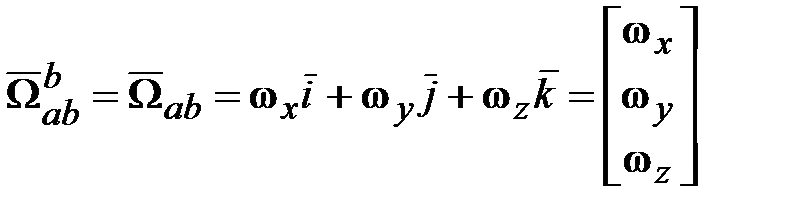 .
.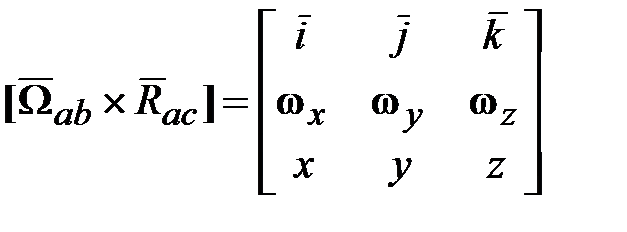 , а также записи
, а также записи 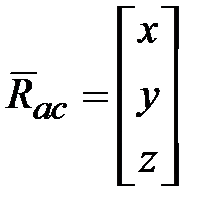 и
и 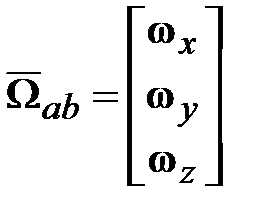 , получим выражение для кинетического момента
, получим выражение для кинетического момента 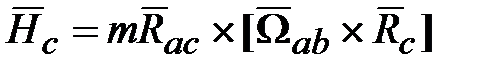 следующим образом.
следующим образом.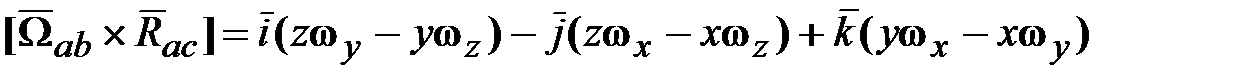 .
.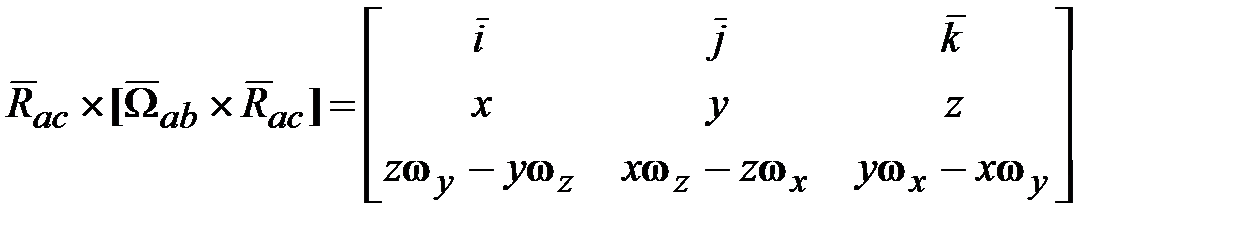
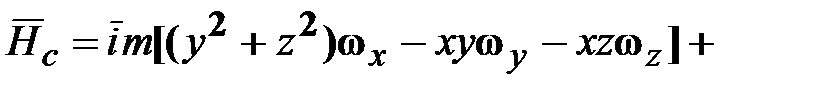
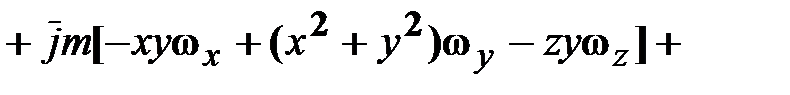
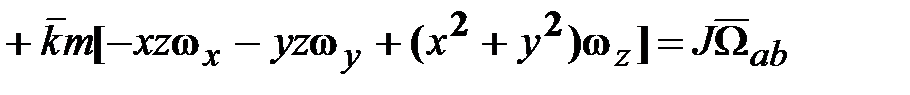 , (18.11)
, (18.11)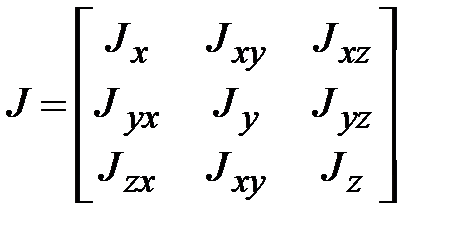 ‒ тензор инерции с элементами
‒ тензор инерции с элементами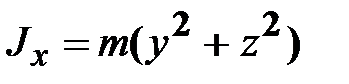 ;
; 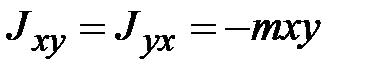 ;
;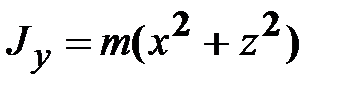 ;
; 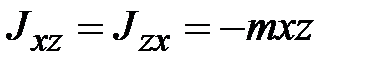
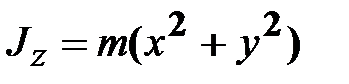 ;
; 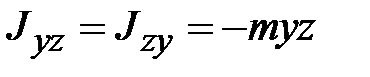 ;
;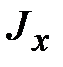 ,
, 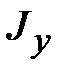 и
и 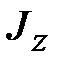 ‒ моменты инерции относительно осей x, y и z, соответственно;
‒ моменты инерции относительно осей x, y и z, соответственно;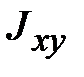 ,
, 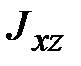 и
и 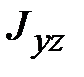 ‒ центробежные моменты инерции.
‒ центробежные моменты инерции. является вещественной, симметричной матрицей, то существует преобразование поворота, приводящее эту матрицу к диагональному виду, т.е. обращающее в нуль все центробежные моменты инерции. Соответствующая СК называется системой главных осей инерции тела. В этом случае выражение (18.11) принимает вид:
является вещественной, симметричной матрицей, то существует преобразование поворота, приводящее эту матрицу к диагональному виду, т.е. обращающее в нуль все центробежные моменты инерции. Соответствующая СК называется системой главных осей инерции тела. В этом случае выражение (18.11) принимает вид: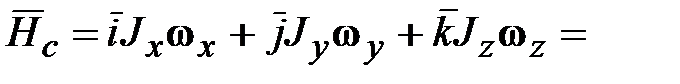
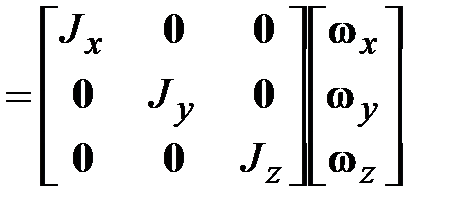 . (18.12)
. (18.12)


