
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема урока: механика. Динамика колебательного движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Иванова М.Г. Учитель физики высшей категории ГОУ СОШ №54 Москва
Продолжаем разговор о гармонических колебаниях. Вы помните, что динамика – это наука о том, почему тело движется. Придумана она выдающимся английским ученым Исааком Ньютоном, и вы помните, что главные действующие лица – это три закона Ньютона. Мы коснемся сегодня второго закона Ньютона, без него описать движение точки невозможно. Так как вы поняли, что гармоническое колебание – это сложный процесс, то мы описываем сложный процесс всегда индуктивным способом, от простого к сложному. Самое простое, что есть в физике, – это модели, которые придуманы для облегчения реальных задач. Первая модель, которую мы сегодня будем рассматривать, – математический маятник. Математический маятник – это небольшое тело, подвешенное на очень длинной невесомой и нерастяжимой нити. В положении равновесия тело находится в точке пространства О, и обеспечивает это положение равновесия равенство двух сил – силы натяжения нити и силы тяжести. На тело, подвешенное на нити, действуют два других тела, и это действие в динамике описывается двумя силами. В таком положении равенство сил обеспечено. Если мы отведем тело от положения равновесия, то произойдет интересная вещь. Сила тяжести останется по модулю точно такой, сила натяжения изменится, и так как действие этих сил будет не вдоль одной прямой, то мы получим равнодействующую этих сил. С помощью метода сложения двух векторных величин, с помощью параллелограмма мы получаем равнодействующую, направленную к центру картинки или к точке равновесия. Помним по второму закону Ньютона: сила равнодействующая определяет направление и модуль ускорения. Коэффициентом пропорциональности выступает масса тела. Давайте найдем эту величину равнодействующей силы. Условимся, что сила тяжести, не меняющаяся во времени, нас вполне устраивает, и мы ее можем найти, т.к. знаем массу и ускорение свободного падения. Тогда модуль этой равнодействующей силы в этом треугольнике выступает в качестве катета противолежащего этому углу, который назовем a. Этот угол a в геометрии этого треугольника, который в пространстве описывает реальное тело, вам понятен по построению. Значит, равнодействующая сила равна гипотенузе, умноженной на синус противолежащего угла. Гипотенуза у нас представлена силой тяжести, поэтому понятно, откуда я это взяла. Величина угла и синус этого угла будет зависеть от величины a напрямую. Чем больше угол отведения от положения равновесия, тем больше синус, тем больше равнодействующая сила. Поэтому у нас возникает внутри системы эта сила равнодействующая, которую мы будем называть внутренняя сила системы, которая напрямую зависит от того, как далеко мы отводим тело от положения равновесия. По второму закону Ньютона Так как у нас sin a выражается из этого треугольника, как противолежащий катет относится к гипотенузе, поэтому здесь вместо sin a поставили S (это отклонение точки от положения равновесия) и l (это длина нити, которая выступает в качестве гипотенузы). Дальше производим преобразования следующего плана. Из этого уравнения видим, что Т.к. эта величина зависит от g (ускорения свободного падения), которое фиксированное для данной точки наблюдения от положения на земном шаре. Т.к. единственные пока известные нам существа, которые исследуют природу, – это люди, то эта величина постоянная для данной точки. Длина маятника не меняется в процессе эксперимента, поэтому мы понимаем, что эта частота для данной системы всегда фиксирована. Создавая такую систему, можем сразу написать ее характеристику – собственную частоту. Обращаю внимание вот на что: собственная частота нашей модели математического маятника не зависит от ее массы. И это парадоксально, но напоминаю, что это модель, поэтому чтобы пользоваться вот этими соотношениями, необходимо соблюдать главные условия: длина маятника была большая, а масса была незначительная. И масса подвеса была несравнима бы намного меньше массы этого маятника. И главное – формула, которая получается, которая необходима для описания движения, – это формула периода математического маятника, которую вывел современник Ньютона Гюйгенс, записывается таким образом: Переходим к следующей модели – модель пружинного маятника. Представим себе тело на пружине, которое совершает колебания под действием этой упругой силы. В момент, когда система предоставлена сама себе, настанет такой момент, когда сила упругости и сила тяжести будут уравновешены. И так это будет проходить достаточно долго, соблюдаться достаточно долго, и это вы можете наблюдать. Если мы в систему внесем некоторое количество энергии разным способом, отведем его от положения равновесия, то этот груз начинает на пружине совершать колебания, переходя из одного положения в другое. И обязательно это положение равновесия будет проходить по инерции. Вот вам первый закон Ньютона, я думаю, что вы понимаете, как все происходит. Силы упругости, вы помните из предыдущего курса механики, выражается законом Гука, как -К . х, где Х – это величина деформации пружины, а К – это жесткость пружины, которая заложена в самой системе. Все зависит от того, какое мы тело для наблюдения выбрали. Тогда сила упругости – это будет возвращающая сила в систему, которая будет меняться от координаты. Сила тяжести в процессе движения не меняется и поэтому на движение тела не влияет. Тогда ускорение, которое будет получать тело в процессе движения, будет прямо пропорционально силе упругости: Производим те же самые замены, из этого второго закона Ньютона выражаем ускорение: «Сокращение на x» - не очень правильный математический термин, потому что x иногда принимает 0 значение, пока вы еще не умеете делить на это, но очевидно, что Х принимает одни и те же значения, поэтому Обратите внимание: по форме эти формулы похожи – и это очень важно, потому что физики всегда стремятся к некой систематизации и рады, когда получаются зависимости, похожие один на другой. Значит, выбор описания пока верен и теория Ньютона подтверждается.
Сегодня мы будем делать лабораторную работу, которая называется «Измерение ускорения свободного падения с помощью математического маятника». Это важная тема в данной главе, мы говорили в п. 3 о том, что эту формулу для вычисления периода математического маятника
Формула вот Здесь помечаю, что это длина маятника, выраженная в метрах, как нужно нам в системе СИ, измерили мы ее с помощью рулетки, l = 0,352 м = 35,3 см.
Итак, начинаем вычисление. Запускаем маятник, запускаем секундомер. Мы провели измерения, давайте запишем их в таблицу. Было 6 колебаний полных, все это происходило за 7,21 с. Если мы сейчас разделим период, получится 1,20 с точностью до сотых. Теперь вычислим ускорение свободного падения по формуле. Вы знаете, что ускорение на нашей широте 9,8 м/с2. У нас получилось немного меньше, но и измерения некоторой неточностью происходят. Есть системные ошибки, есть приборные ошибки, поэтому, чтобы повысить точность эксперимента, необходимо сделать несколько вычислений, что вы могли бы сделать дома, пользуясь собственным секундомером. При округлении этой величины и 9,8 мы получаем 10, т.е. мы используем всегда 10 м/с2. Для наших несерьезных экспериментов этого достаточно. Надеюсь, вам было все понятно и вы научились измерять важную физическую величину. Спасибо за внимание.
Мы продолжаем изучать раздел физики – «Механика». Мы находимся в 7-й главе «Колебания и волны». Сегодня нам предстоит познакомиться с упругой средой, которая испытывает на себе процессы, которые называются механические волны. Мы разберем не только волны, виды волн, но и количественные характеристики – длину волны и скорость распространения. Чтобы рассматривать волну предметно, давайте введем новое определение, которое называется упругая среда. Значит, если в среде между частицами существуют силы взаимодействия, то такую среду мы будем называть упругой. Упругие свойства начинают проявляться, когда мы деформируем какую-то часть этой среды. Начинаем деформировать, в одном месте частицы получают какой-то импульс от нас, и они передают этот импульс от точки к точке, от молекулы к другой молекуле. Давайте дадим определение механической волны. Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной колеблющейся точки к другой. Вы такое не раз пробовали провести с упругой средой: вы, стоя на берегу, бросали в воду камни. Тогда камень становился источником упругой деформации волны. Понимаете, что вслед за камнем, который притягивает к себе земля, эта среда упругая, потому что молекулы воды между собой связаны силами взаимодействия, их очень много, они достаточно большими силами взаимодействия связаны. Когда вслед за камнем точки воды начинают двигаться вниз, то они увлекают за собой соседние молекулы, и этот процесс распространяется во времени. Вы этот процесс видели – доходит до вас, до берега это возмущение упругой среды. Я хочу еще обратиться к вашему жизненному опыту: если осенью на поверхности воды будем наблюдать листочек, то, когда волна распространяется, листок сразу к берегу вслед за волной не перейдет. Поэтому он начинает вслед за волной совершать колебательные движения вверх-вниз. Поэтому передачи вещества в механических волнах нет, а есть только передача энергии. Это очень важное для понимания процесса, очень важное умозаключение. Давайте разберем, какие волны встречаются в природе и в быту. Волны разделяют на поперечные и продольные. Поперечная волна вызывается на воде, которую мы только что рассмотрели. И вдоль шнура, сейчас я вам это покажу. Давайте представим, что будет происходить с резиновым шнуром, закрепленным к стене, если конец этого шнура поднимать и опускать, чередуя действия вверх-вниз. По шнуру распространится волна, и распространение колебаний будет идти в эту сторону, а колебательный процесс будет идти поперек этого направления. Такую волну называют поперечной. Давайте посмотрим, как я сделаю эту волну поперечную. У меня в руках резиновый шнур. Он упругий, частицы связаны между собой, он – упругая среда, и я буду вызывать в нем колебания, волну, которая будет распространяться, совершая следующие действия. Буду вверх и вниз поднимать руку – посмотрите, что произойдет. Волна распространяется от меня к стене, а колебание в упругой среде происходит перпендикулярно этому направлению. Сейчас я это буду делать медленно. А сейчас я это сделаю быстро. Запомним это наблюдение. Значит, такая волна называется поперечная. Если мы возьмем пружину большую, закрепим ее около стены и вызовем колебания простым толчком с одной стороны этой пружинки, то произойдет интересная вещь. В каких-то моментах появится сжатие пружины, а в некоторых будет растяжение. Все опять обусловлено тем, что молекулы связаны между собой и импульс от одной молекулы передается к другой. При этом колебание частиц пружины будет происходить в том же направлении, в котором и происходит распространение волны. Я это здесь нарисовала схематично. Распространение волны идет слева направо, а направление колебания этой точки будет происходить тоже слева направо, вдоль распространения волны. Такую волну называют продольной. Я сейчас ее вам тоже покажу. На примере такой пружины. Хоть пружина и провисла, направление колебания пружины будет происходить вдоль нее. Повторим, по-моему, хорошо заметно, что точки среды не смещаются в пространстве, а совершают колебательные движения около своей точки равновесия. Если поперечные волны мы можем увидеть на воде и вдоль резинового шнура, то продольные волны вы знаете хорошо и активно ими пользуетесь. Например, звуковые волны, они тоже продольные. Посмотрите, что происходит, когда эта девушка говорит молодому человеку что-то на расстоянии. Процесс происходит только в упругой среде, когда между ними есть посредник, воздух, например. Голосовые связки создают в воздушном зазоре между ухом (приемником волны) и источником волны разные части сжатия волны и разряжения. Они чередуются. Понятное дело: распространение волны идет слева направо на этом чертеже, вот так. Изменение колебаний точек среды происходит тоже вдоль этого направления. Я думаю, что вас убедила, это колебание продольное. И широко распространенное колебание, которое вы знаете в тепловых двигателях, – это колебание поршня в цилиндре. Когда цилиндр заполнен газом или жидкостью. Например, в наших двигателях внутреннего сгорания поршень совершает почти гармонические колебания, такое колебание мы можем расценивать как источник этого колебательного движения, при этом среда упругая жидкости или газа, которая в цилиндре находится, будет испытывать действие этого вибратора и будет по нему распространяться продольная механическая волна. Давайте подумаем и разберем, какими характеристиками описывают поведение волны. Под третьим пунктом у нас будет длина волны и скорость волны. Представим себе, что мы дважды сфотографировали волну. Первый раз, когда бросили камень. Эта толстая линия показывает распространение волны в первый момент. Вот волна распространилась, мы ее сфотографировали. Потом посмотрели, когда эта точка сместилась на некоторую величину вниз от первоначального положения, и проследили за ней. Волна вот так распространяется. Давайте подумаем, как эта точка А, которая до возмущения волны находилась здесь. После того как волна в первый момент времени t занимала такое положение, точка А сместилась сюда относительно оси х. Через некоторое время ∆t эта точка поднимается наверх и занимает такое положение. При этом она тоже на этой волне оказывается. Точка В, которая занимала положение такое, через ∆t окажется здесь. Все точки среды постоянно колеблются вверх-вниз относительно положения равновесия. Если волна не сильно затухает, то максимальная амплитуда у точки А и у точки В одинаковая. Отклоняется на х вверх, отклоняется на х вниз. Волна распространяется от этой точки, это мы нарисовали график изменения координаты точки по оси х и взяли такой большой кусок в пространстве длиной S. Понятное дело, что из этой точки волна распространяется сюда, и мы знаем и заметили, что распространение может быть с разными скоростями. Чуть позже будет понятно, что мы под скоростью волны понимаем. Первая физическая величина, которая описывает волну, называется длина волны. Обозначается она буквой l, греческой буквой l, это строчная буква, в одну клеточку ее можно вписать, это расстояние от этой точки до этой точки. Что это за точка? Эта точка, как и эта, колеблется с ней в одинаковых фазах. Обратите внимание, сейчас эта точка до среды и эта занимают одинаковое положение. Через ∆t она сместится сюда и эта точка тоже сместится сюда. Вот что значит «колеблется в одинаковых фазах». l = [м] – длина волны – расстояние между ближайшими точками, колеблющимися в одинаковой фазе. Понятно, что таких точек много можно найти в процессе распространения волны, поэтому l выбрана как ближайшее расстояние между ними. Измеряется в системе СИ длина в метрах и связана с той величиной, о которой мы знаем из раздела 3, который называют «Криволинейное движение», связана с периодом колебаний и со скоростью распространения таким образом, l = V . Т. Эта формула подходит и для описания волновых процессов. Давайте посмотрим, что такое скорость волны. Оказывается, скорость волны связана с длиной волны так: V = ln - где буквой n греческая обозначена частота. Частота – это количество колебаний точки среды в единицу времени. Какая у нас единица времени в системе СИ выбрана? Какой промежуток времени выбран за единицу? Секунда. Если мы посчитаем, сколько за секунду колебаний совершит точка среды, – это и будет частота. Если эту частоту домножим на l, получим скорость распространения волны. Мы знаем, что самая распространенная волна – волна звуковая. Какова скорость распространения звуковой волны в среде, в воздухе? Очень сильно зависит от того, в каком состоянии находится среда. Если воздух прогрет до 20 °С, то скорость распространения волны примерно 336 м/с. Если среда становится более уплотненной, то скорость повышается. Вы это хорошо знаете из сказок и бытовых ситуаций. Напомню вам: наверняка вы когда-нибудь ночевали вблизи железнодорожного полотна или асфальтовой дороги, по которой всю ночь ездят грузовики. Спокойнее спать всегда, когда воздух не сырой, не наполненный водяными парами, т.е. более разреженный. Если это происходит после дождя, то все сигналы, которые подают движущиеся объекты на полотне, слышно хорошо. Не успевает сигнал ослабнуть и приходит к нам достаточно серьезный и сильный, с большой амплитудой. Введем еще некие характеристики, которые необходимы для более серьезного изучения волны. Например, что такое луч. Чтобы ввести понятие луч, нужно обратиться к воображению и ввести понятие, которое называется волновой фронт. Все точки среды, в которой распространяется волна, которые колеблются с одинаковой фазой, геометрическое место точек образует одну поверхность, которая называется волновой фронт. Если мы по воде будем стучать палочкой, то волны будут иметь такую конфигурацию. Все эти части, бугорки, которые я нарисовала, волн будут называться волновой поверхностью. Луч, линия, которая перпендикулярна волновой поверхности и будет нам показывать направление распространения волны. Я и написала, что луч – это линия перпендикулярная волновой поверхности и что луч показывает направление распространения волны. Итак, урок по волнам закончен, надеюсь, вам было все понятно. Продолжаем изучать механику. Мы находимся в главе 7, «Колебания и волны». Параграф 7, который сегодня посвящен звуковым волнам. Звуковые волны – это особые волны, которые вызывают колебания среды, которые воспринимаются нашим органом слуха – ухом. Раздел, который занимается в физике этими волнами, называется акустика. Профессия людей, которых в простонародье называют слухачами, называют акустиками. Звуковая волна – это волна, распространяющаяся в упругой среде, это продольная волна, и, когда она распространяется в упругой среде, у нас чередуются сжатие и разряжение. Передается она с течением времени на расстояние. К звуковым волнам относятся такие колебания, которые осуществляются с частотой 20 Гц и 20 тыс. Гц. Я написала, что этот диапазон будет называться слышимый звук. Этим длинам волн соответствует в той среде, о которой мы говорили, воздух при t = 20 °C соответствует 17 м длина волны и 20 тыс. Гц частота – 17 мм. Существуют еще такие диапазоны, которыми занимаются акустики, – инфразвуковые и ультразвуковые. Инфразвуковые – это те, которые имеют частоту меньше 20 Гц. И ультразвуковые – это те, которые имеют частоту больше 20 тыс. Гц. Каждый образованный человек должен ориентироваться в диапазоне частот звуковых волн и знать, что если он пойдет на УЗИ, то картинка на экране компьютера будет строиться с частотой больше 20 тыс. Гц. Инфразвук – тоже важные волны, которые используют для колебаний поверхности (например, чтобы разрушить какие-нибудь большие объекты). Мы запускаем инфразвук в почву – и почва дробится. Где такое используется? Например, на алмазных приисках, где берут руду, в которых есть алмазные компоненты, и дробят на мелкие частицы, чтобы найти эти алмазные вкрапления. Значит, скорость звука зависит от условий среды и температуры. Я специально выписала эти важные расхождения, которые происходят с волной, если мы берем другую среду или увеличиваем температуру. Посмотрите, в воздухе скорость звука при t=0 °C V= 331 м/с, при t=1 °C скорость увеличивается на 1,7 с. Если вы – исследователь, то вам могут пригодиться такие знания. Вы, может быть, даже придумаете какой-нибудь температурный датчик, который будет фиксировать или будет расхождения температуры мерить путем изменения скорости звука в среде. Я говорила: чем плотнее среда, чем более серьезное взаимодействие между частицами среды, тем быстрее распространяется волна. Мы в прошлом параграфе обсудили это на примере воздуха сухого и воздуха влажного. Посмотрите, в воде скорость, для воды V = 1400 м/с. Звук, если мы его будем распространять (стучать по камертону, например, или по железке каким-нибудь предметом в воде и в воздухе), то скорость распространения увеличивается почти в 4 раза. По воде информация дойдет быстрее в 4 раза, чем по воздуху. А в стали и того быстрее, посмотрите, V = 5000 м/с = 5 км/с. Я, чтобы вы это запомнили, специально написала такой маячок – Илья Муромец. Вы знаете из былин, что Илья Муромец пользовался (да и все богатыри, да и обычные русские люди и мальчики РВС Гайдара), пользовались очень интересным способом обнаружения объекта, который идет далеко еще, приближается, но располагается еще далеко. Звук, который он издает при движении – поезд либо конница вражеская, еще не видно и не слышно этой конницы. Илья Муромец, припав ухом к земле, может ее услышать. Почему? Потому что по твердой земле передается звук с большей скоростью, значит, быстрее дойдет до уха Ильи Муромца и он сможет подготовиться к встрече неприятеля. Самые интересные звуковые волны – музыкальные звуки и немузыкальные шумы. Какие предметы могут создать звуковые волны? Если мы возьмем источник волны и упругую среду, если мы заставим источник звука колебаться гармонически, то у нас возникнет замечательная звуковая волна, которая будет называться – звук музыкальный. Вы, знаете эти источники звуковых волн: например, струны у гитары или струны у рояля. Это, может быть, звуковая волна, которая создана в зазоре воздушном трубы (например, органа или трубы, духовых каких-нибудь инструментов). Из уроков музыки вы знаете ноты: до, ре, ми, фа, соль, ля, си. Называются в акустике тоны. Обозначаются такими буквами. Самое удивительное, что все предметы, которые могут издавать тоны, у всех них будут особенности. Чем они различаются? Они различаются длиной волны и частотой. Если эти звуковые волны создаются не гармонически звучащими телами или не связаны в общую какую-то оркестровую пьесу, то такое количество звуков будет называться шумом. Хаотическая смесь звуков – это шум. Понятие шум есть бытовое, есть физическое, оно очень похоже, и поэтому мы его вводим как отдельный важный объект рассмотрения. Переходим к количественным оценкам звуковых волн. Какие у музыкальных звуковых волн характеристики? Эти характеристики распространяются исключительно на гармонические музыкальные колебания. Итак, громкость звука. Чем определяется громкость звука? Я здесь нарисовала распространение звуковой волны во времени или колебания источника звуковой волны. Он располагается здесь и начинает колебаться, при этом колеблется гармонически, вызывает музыкальный звук. При этом, если мы добавили в систему не очень много звука (стукнули тихонечко по ноте фортепиано, например), то будет тихий звук. Если мы громко, высоко поднимая руку, вызовем этот звук, стукая по клавише, получим громкий звук. От чего это зависит? По-моему, всем понятно, что все будет зависеть от амплитуды колебания источника звука. У тихого звука амплитуда колебаний меньше, чем у громкого звука Ат < Агр. Следующая важная характеристика музыкального звука и любого другого – высота. От чего зависит высота звука? Высота зависит от частоты. Мы можем заставить источник колебаться часто, а можем заставить не очень быстро колебаться, совершать за единицу времени меньшее количество колебаний. Посмотрите, как я это математически нарисовала на доске. Первый низкий звук колеблется таким образом. Здесь развертка во времени. Колебания происходят тут, можно заставить струну так колебаться. Мы будем колебания описывать таким образом. При этом то виртуальное, то, чего нету, а есть только в нашем сознании, развертка во времени, мы ее таким образом нарисовали. У меня длина волны одной укладывается в такой промежуток времени. У второй волны я специально амплитуду сделала одинаковой, чтобы громкость звука была одинаковой. Окажется, что если мы умудримся за то же время совершить два колебания источником звука, то звук получится высокий. Поэтому можно сделать интересный вывод. Если человек поет басом, то у него источник звука (это голосовые связки) колеблется в несколько раз медленнее, чем у человека, который, например, женщина, которая поет сопрано. У нее чаще колеблются голосовые связки, поэтому вызывают чаще очаги сжатия и разряжения в распространении волны. Есть еще одна интересная характеристика звуковых волн, которую физики не изучают. Это тембр. Вы знаете и легко различаете одну и ту же музыкальную пьесу, которую исполняют на балалайке или на виолончели. Чем отличаются эти звучания или чем отличается это исполнение? Мы попросили в начале эксперимента людей, которые извлекают звуки, делать их примерно одинаковой амплитуды. Громкость звука чтобы была одинакова. Это так в оркестре, если не требуется выделения какого-то инструмента, все играют примерно одинаково, в одинаковую силу. Так вот тембр балалайки и виолончели отличается, потому что звук, если бы мы его нарисовали, который извлекают из одного инструмента из другого, мы бы нарисовали с помощью диаграмм, то ничем бы не отличался. Но вы легко отличаете эти инструменты по звуку. Еще один пример, почему тембр важен. Два певца, которые заканчивают один и тот же музыкальный вуз, консерваторию, у одинаковых педагогов, учились одинаково хорошо на пятерки. Почему-то один становится выдающимся исполнителем, а другой всю жизнь недоволен своей карьерой, пытается сделать что-то лучше. На самом деле это определяется исключительно их инструментом, который вызывает как раз голосовые колебания в среде, т.е. у них отличаются голоса по тембру. Если тембр голоса таков, что он вызывает у всех остальных людей какие-то сильные эмоции (например, самая простая эмоция – это мурашки по коже бегают), если даже такое физическое изменение среды при передаче от певца к вам в уши этого колебания вызывает у вас изменение кожного покрова, вы можете смело считать, что этот человек – гений.
Итак, завершаем 7 главу – «Колебания и волны» - интересными явлениями. Это отражение волн и звуковой резонанс. Вы знаете, что в пустом помещении, в горах или под сводами здания какой-нибудь арки можно замечательное явление наблюдать – эхо. Что такое эхо? Эхо – это явление отражения звуковых волн от плотных объектов. Когда человек может услышать эхо? Оказывается, чтобы человек смог различить (его слуховой аппарат смог различить два сигнала), необходимо, чтобы запаздывание во времени было 0,06 с. Давайте посчитаем: скорость распространения волны 40 м/с в воздухе, поэтому можно рассчитать расстояние до объекта, от которого будет отражаться волна. Должно быть понятно: при перемножении скорости на эту величину, запаздывания мы получаем 20,4 м. L=V.∆t = 340 м/с 0,06 м/с = 20,4 м.
Но, вы понимаете, что отражение – это движение волны в одну сторону, в другую потом претерпевает отражение, поэтому расстояние, которое мы получили, можно спокойно разделить пополам и поставить человека на расстояние
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 699; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.32.243 (0.017 с.) |

 . Перепишем этот векторный вид второго закона в виде проекционном на ось, которая перпендикулярна в любой момент времени нитям маятника. И тогда ma=-m.g.sina возвращающей силе. Масса слева, масса справа сокращаются, получается вот такой вид.
. Перепишем этот векторный вид второго закона в виде проекционном на ось, которая перпендикулярна в любой момент времени нитям маятника. И тогда ma=-m.g.sina возвращающей силе. Масса слева, масса справа сокращаются, получается вот такой вид.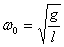 , т.к. S, х – это одна и та же величина, только по-разному обозначена. Это мы в динамике обозначили, а т.к. у нас было в кинематике, т.е. мы по-прежнему переходим к единообразному описанию движения.
, т.к. S, х – это одна и та же величина, только по-разному обозначена. Это мы в динамике обозначили, а т.к. у нас было в кинематике, т.е. мы по-прежнему переходим к единообразному описанию движения. . Это очень важная формула, и ее необходимо запомнить.
. Это очень важная формула, и ее необходимо запомнить.
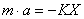 .
.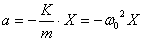 .
. - собственная частота маятника.
- собственная частота маятника. - тоже собственная частота пружинного маятника, и зависит исключительно от того, какую пружинку мы подобрали, жесткость какая у нее, какой груз мы подвесили, т.е. зависит от параметрических значений этой системы колебательной. Тогда период математического маятника связан с циклической частотой, вы помните из кинематики, вот таким соотношением
- тоже собственная частота пружинного маятника, и зависит исключительно от того, какую пружинку мы подобрали, жесткость какая у нее, какой груз мы подвесили, т.е. зависит от параметрических значений этой системы колебательной. Тогда период математического маятника связан с циклической частотой, вы помните из кинематики, вот таким соотношением  . Получаем формулу для расчета периода пружинного маятника
. Получаем формулу для расчета периода пружинного маятника  .
. . Вместо длины маятника сразу, т.к. она фиксированная константа, пишем 0,352,
. Вместо длины маятника сразу, т.к. она фиксированная константа, пишем 0,352,  .
. от преграды, от которой будет отражаться звук, и тогда можно эхо услышать. Нужно еще хорошо отражающую поверхность, потому что, если, например, комната достаточно большая, она заставлена большим количеством мебели (мягкой мебели) и людьми, то все эти объекты поглощают звуковую волну, поэтому эхо неразличимо. Просто энергии не хватает для звуковой волны, чтобы было это явление. Где это явление используют? Конечно, занимательно слушать эхо в горах, здорово петь под музыкальными арками, которые в архитектуре XIX века часто используются, но есть реальные устройства, которые используют это свойство. Например, рупор. Если я сейчас сложу вот так ладошки, вы сразу услышали, что мой звук стал мощнее, хотя люди, которые стояли бы у меня сбоку, звук от моих голосовых связок был бы намного тише. Поэтому происходит интересное явление: стенки рупора усиливают звуковую волну, увеличивая мощность сигнала. Что такое эхолот? Это сложное слово, полученное из двух слов: «эхо» – «отражение», «лот» – прибор, который мерит глубину водоема. Лот – это простой камень на веревке у рыбаков. Эхолот у людей, которые плавают на больших суднах, устроен следующим образом. Под бортом корабля располагается приемник и источник звуковых волн. От источника звуковых волна идет звуковая волна, доходит до дна, отражается и попадает в приемник звуковых волн. Время фиксируется, которое проходит между подачей сигнала и приходом его обратно. ∆ t = 0,06 с. И расстояние, которое получается вот таким расчетом,
от преграды, от которой будет отражаться звук, и тогда можно эхо услышать. Нужно еще хорошо отражающую поверхность, потому что, если, например, комната достаточно большая, она заставлена большим количеством мебели (мягкой мебели) и людьми, то все эти объекты поглощают звуковую волну, поэтому эхо неразличимо. Просто энергии не хватает для звуковой волны, чтобы было это явление. Где это явление используют? Конечно, занимательно слушать эхо в горах, здорово петь под музыкальными арками, которые в архитектуре XIX века часто используются, но есть реальные устройства, которые используют это свойство. Например, рупор. Если я сейчас сложу вот так ладошки, вы сразу услышали, что мой звук стал мощнее, хотя люди, которые стояли бы у меня сбоку, звук от моих голосовых связок был бы намного тише. Поэтому происходит интересное явление: стенки рупора усиливают звуковую волну, увеличивая мощность сигнала. Что такое эхолот? Это сложное слово, полученное из двух слов: «эхо» – «отражение», «лот» – прибор, который мерит глубину водоема. Лот – это простой камень на веревке у рыбаков. Эхолот у людей, которые плавают на больших суднах, устроен следующим образом. Под бортом корабля располагается приемник и источник звуковых волн. От источника звуковых волна идет звуковая волна, доходит до дна, отражается и попадает в приемник звуковых волн. Время фиксируется, которое проходит между подачей сигнала и приходом его обратно. ∆ t = 0,06 с. И расстояние, которое получается вот таким расчетом,  делится пополам, и мы находим глубину водоема. Используются эхолоты не только на звуковых частотах, но и на инфразвуке или на ультразвуке. Мы в прошлом параграфе говорили, как это используется. Принцип один и тот же. Используется явление отражения звуковых волн. Давайте рассмотрим еще одно интересное звуковое явление – это звуковой резонанс. Напоминаю: это явление увеличения амплитуды вынужденных колебаний при соблюдении частоты собственных колебаний системы и вынужденных. Напоминаю: любая система, которая может колебаться, имеет собственную частоту. Эта частота сформирована самой конструкцией прибора, который умеет колебаться. Если мы этот прибор заставим колебаться с внешней силой, которая имеет вот такую частоту вынужденных колебаний n0 = nВЫН, произойдет усиление звуковых колебаний, потому что увеличение амплитуды влечет за собой усиление звука, мощности энергетической. Чтобы объяснить это явление подробно, чтобы вы поняли, что значит резонанс, мы будем работать с таким специальным прибором, который используется в музыке. Этот прибор называется камертон. Вилочка сделана из стали, имеет собственную частоту, соответствующую в данном опыте ноте ля. К этому камертону подобран специальный, путем проб и ошибок, путем вычислений математических, резонаторный ящик. Что это за ящик такой? Что он делает со звуком, мы сейчас с вами увидим на опыте. Перед нами камертон. У меня есть резиновый молоточек, которым мы будем вызывать колебания. У этого камертона колебания будут вынужденные. Вот сначала, чтобы понять, для чего нужен резонаторный ящик, я попробую прикрывать простым листом бумаги резонаторный ящик вот так. Слушайте внимательно, что будет происходить с самим звуком. Если вы что-то заметили, давайте повторим еще раз опыт. Я попробую вызвать более серьезное колебание, увеличив энергию в системе. Итак, резонаторный ящик увеличивает амплитуду результирующих колебаний. Как он это делает? Он перераспределяет энергию, которую я сообщила в систему. Значит, камертон вызывает в резонаторном ящике колебание самой деки ящика и воздуха, который находится внутри этого ящика. Колебания складываются и усиливают звук. При этом у нас закон сохранения энергии выполняется, т.е. с резонаторным ящиком камертон звучит меньше по времени, но зато сильнее. Продолжим эксперимент. Давайте посмотрим, как можно колебание это звуковое прекратить. Я коснулась ножек камертона, и коэффициент затухания у данной системы очень большой стал, колебание прекратилось практически мгновенно. Повторим, колебаний нет. Теперь мы посмотрим явление резонанса, что произойдет, если я возьму точно такой, имеющий точно такую звуковую частоту, другой камертон. Посмотрите, резонаторные ящики будут направлены друг на друга, чтобы зазор воздушный был незначительный и чтобы не затухали колебания, и эффект был максимальный. Итак, вызываю колебания вот в этом камертоне. Звуковая
делится пополам, и мы находим глубину водоема. Используются эхолоты не только на звуковых частотах, но и на инфразвуке или на ультразвуке. Мы в прошлом параграфе говорили, как это используется. Принцип один и тот же. Используется явление отражения звуковых волн. Давайте рассмотрим еще одно интересное звуковое явление – это звуковой резонанс. Напоминаю: это явление увеличения амплитуды вынужденных колебаний при соблюдении частоты собственных колебаний системы и вынужденных. Напоминаю: любая система, которая может колебаться, имеет собственную частоту. Эта частота сформирована самой конструкцией прибора, который умеет колебаться. Если мы этот прибор заставим колебаться с внешней силой, которая имеет вот такую частоту вынужденных колебаний n0 = nВЫН, произойдет усиление звуковых колебаний, потому что увеличение амплитуды влечет за собой усиление звука, мощности энергетической. Чтобы объяснить это явление подробно, чтобы вы поняли, что значит резонанс, мы будем работать с таким специальным прибором, который используется в музыке. Этот прибор называется камертон. Вилочка сделана из стали, имеет собственную частоту, соответствующую в данном опыте ноте ля. К этому камертону подобран специальный, путем проб и ошибок, путем вычислений математических, резонаторный ящик. Что это за ящик такой? Что он делает со звуком, мы сейчас с вами увидим на опыте. Перед нами камертон. У меня есть резиновый молоточек, которым мы будем вызывать колебания. У этого камертона колебания будут вынужденные. Вот сначала, чтобы понять, для чего нужен резонаторный ящик, я попробую прикрывать простым листом бумаги резонаторный ящик вот так. Слушайте внимательно, что будет происходить с самим звуком. Если вы что-то заметили, давайте повторим еще раз опыт. Я попробую вызвать более серьезное колебание, увеличив энергию в системе. Итак, резонаторный ящик увеличивает амплитуду результирующих колебаний. Как он это делает? Он перераспределяет энергию, которую я сообщила в систему. Значит, камертон вызывает в резонаторном ящике колебание самой деки ящика и воздуха, который находится внутри этого ящика. Колебания складываются и усиливают звук. При этом у нас закон сохранения энергии выполняется, т.е. с резонаторным ящиком камертон звучит меньше по времени, но зато сильнее. Продолжим эксперимент. Давайте посмотрим, как можно колебание это звуковое прекратить. Я коснулась ножек камертона, и коэффициент затухания у данной системы очень большой стал, колебание прекратилось практически мгновенно. Повторим, колебаний нет. Теперь мы посмотрим явление резонанса, что произойдет, если я возьму точно такой, имеющий точно такую звуковую частоту, другой камертон. Посмотрите, резонаторные ящики будут направлены друг на друга, чтобы зазор воздушный был незначительный и чтобы не затухали колебания, и эффект был максимальный. Итак, вызываю колебания вот в этом камертоне. Звуковая 


