
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметры поступательного движения.Содержание книги Поиск на нашем сайте Поступательное движение — это механическое движение системы точек (абсолютно твёрдого тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени
Поступательно движется, например, кабина лифта. Также, в первом приближении, поступательное движение совершает кабина колеса обозрения. Однако, строго говоря, движение кабины колеса обозрения нельзя считать поступательным. В соответствие с первым и вторым законами Ньютона кабина, стремясь сохранить направление своего движения, отклоняется от вертикальной прямой, причём в разном направлении по разные стороны от оси симметрии колеса обозрения. Таким образом, не всякая прямая, связанная с кабиной, перемещается параллельно самой себе. Причём отклонение кабины от вертикальной прямой, и соответственно, отклонение траектории движения кабины от траектории поступательного движения тем больше, чем больше частота вращения колеса обозрения. Учитывая, что реальные частоты вращения колёс обозрения достаточно малы, траектории движения их кабин весьма близки к траектории поступательного движения. Этим можно объяснить, что во многих источниках движение кабины приводится в качестве примера поступательного движения. Моделью поступательного движения в первом приближении (если пренебречь качанием ступни) является педаль велосипеда, совершающая при этом за полный цикл своего хода один поворот вокруг своей оси. Параметры вращательного движения Враща́тельное движе́ние — вид механического движения. При вращательном движении материальной точки она описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна. При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым. Полярные векторы - истинные векторы, т.е. которые обладают действительным, а не условным направлением (т.е. Аксиальные векторы - угловые векторы, направление которых связано с направлением вращения; понятие вводится для наглядности, упрощения расчетов (рассматриваемые ниже угловые кинематические параметры относятся к аксиальным векторам).
1) его модуль равен углу поворота 2) направление определим как совпадающее с осью вращения по правилу правого винта по отношению к
Размерности угловых кинематических параметров в системе СИ следующие:
При
Задачи кинематики вращательного движения:
Аксиомы динамики Содержание темы: Основные аксиомы динамики. Понятие о трении и коэффициенте полезного действия. Работа и мощность при поступательном и вращательном движении. Потенциальная и кинетическая энергия. Моменты инерции однородных тел. Динамика есть часть теоретической механики, изучающая механическое движение тел в зависимости от сил, влияющих на это движение. Динамика основывается на ряде положений, являющихся аксиомами и называющимися законами динамики. Первый закон динамики, называемый аксиомой инерции или первым законом Ньютона, в применении к материальной точке формулируется так: изолированная материальная точка либо находится в покое, либо движется прямолинейно и равномерно. Было установлено, что при прямолинейном равномерном движении ускорение материальной точки равно нулю, т.е. изолированная материальная точка не может сама себе сообщить ускорение. Это свойство тел называется инерцией или инертностью. Можно сказать, что инерция или инертность есть способность тела сохранять свою скорость по модулю и направлению неизменной, в том числе и скорость равную нулю. Изменить скорость, т.е. сообщить ускорение, может лишь приложенная к телу сила.. Зависимость между силой и сообщаемым этой силой ускорением устанавливает второй закон динамики или второй закон Ньютона: ускорение, сообщаемое материальной точке силой, имеет направление силы и пропорционально ее модулю Сила Инерции Си́ла ине́рции (также инерционная сила) — многозначное понятие, применяемое в механике по отношению к трём различнымфизическим величинам. Одна из них — «даламберова сила инерции» — вводится в инерциальных системах отсчёта для получения формальной возможности записи уравнений динамики в виде более простых уравнений статики. Другая — «эйлеровасила инерции» — используется при рассмотрении движения тел в неинерциальных системах отсчёта. Наконец, третья — «Ньютонова сила инерции» — сила противодействия, рассматриваемая в связи с третьим законом Ньютона[1][2][3]. Общим для всех трёх величин является их векторный характер и размерность силы. Кроме того, первые две величины объединяет возможность их использования в уравнениях движения, по форме совпадающих с уравнением второго закона Ньютона[1].
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1890; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 ,
,  ,
,  ).
). - бесконечно малый угол, который охарактеризуем вектором:
- бесконечно малый угол, который охарактеризуем вектором: ,
, .
. - угловая скорость
- угловая скорость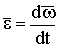 - угловое ускорение
- угловое ускорение ,
,  ,
,  .
.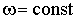 :
: - круговая частота вращения твердого тела вокруг оси
- круговая частота вращения твердого тела вокруг оси - период вращения
- период вращения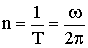 - линейная частота вращения
- линейная частота вращения ,
,  - проекции
- проекции  ,
,  на ось вращения
на ось вращения 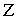

 найти проекции
найти проекции  ,
,  в любой момент времени.
в любой момент времени. - известна
- известна  ,
,  ,
,  .
.



