
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определить ускорение свободного падения методом оборотного и математического маятников.Содержание книги
Поиск на нашем сайте
ЛАБОРАТОРНАЯ РАБОТА
«Свободные колебания механических Систем» Цель работы: Изучить не изохронные колебания физического и математического маятников; Определить ускорение свободного падения методом оборотного и математического маятников.
ЭЛЕМЕНТЫ ТЕОРИИ
1. СВОБОДНЫЕ КОЛЕБАНИЯ Колебательные явления играют важную роль в самых разнообразных явлениях природы и технических устройствах. Рассмотрим колебательные системы с одной степенью свободы. Мгновенное положение колебательной системы с одной степенью свободы может быть определено с помощью какой-либо одной величины Производная по времени от обобщенной координаты называется обобщенной скоростью В случае колебательных систем с малым трением, диссипацией энергии можно пренебречь, и считать, что полная энергия системы сохраняется во времени. Тогда
Решение этого уравнения имеет вид:
Величина Уравнение (1.2) содержит две произвольные постоянные:
2. ТИПОВЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ. Для определения характера движения механической системы нужно, применяя законы динамики или закон сохранения (превращения) энергии, составить уравнение движения системы, и если оно имеет вид (1.1), то данная система является гармоническим осциллятором, колеблющемся по закону (1.2); при этом частота колебаний Пружинный маятник Пружинный маятник представляет собой систему, состоящую из груза массой
Рис. 1. Пружинный маятник.
Получим уравнение незатухающих колебаний (в отсутствие трения в системе) пружинного маятника двумя способами: из законов динамики и из закона сохранения энергии.
Получили дифференциальное уравнение гармонических колебаний
Как видно из формулы (2.1) период колебаний пружинного маятника не зависит от амплитуды колебаний
Математический маятник. Математический маятник представляет собой материальную точку массой Выведем уравнение собственных колебаний математического маятника.
Колебания математического маятника будут изохронными при условии малости отклонений маятника от вертикали
Физический маятник Физическим маятником называется твердое тело, способное совершать колебания под действием силы тяжести относительно горизонтальной оси, проходящей через точку подвеса О перпендикулярно плоскости колебаний (рис. 3).
Рис. 3. Физический маятник.
Роль обобщенной координаты Получим уравнение свободных незатухающих колебаний физического маятника динамическим и энергетическим методами.
Таким образом, получили дифференциальное уравнение колебаний физического маятника
Из вида полученного уравнения можно заключить, что колебания физического маятника, так же как и математического маятника, не являются изохронными. Только при выполнении условия Найдем решение уравнения (2.3). Так как угловая скорость вращения маятника
Интегрируя (2.4)
Так какугловая скорость вращения
Отсюда
Учитывая, что период колебаний маятника
Таким образом, период колебаний физического маятника зависит от угловой амплитуды колебаний Интеграл в формуле (2.8) не может быть вычислен в элементарных функциях. Для его расчета используют табулированные функции эллиптических интегралов или численные методы, встроенные в математические пакеты. Как указывалось выше, колебания физического маятника приближенно можно считать изохронными, если угловая амплитуда маятника не превышает нескольких градусов, то есть выполняется условие
Из (2.9) следует, что частота гармонических колебаний физического маятника равна
Сравнивая формулы (2.10) и (2.2) можно заключить, что физический маятник колеблется так же, как и математический маятник с длиной
которая называется приведенной длиной физического маятника. Для не изохронных колебаний данное утверждение также справедливо. Отложим от точки подвеса О вдоль прямой ОС отрезок ОО´, длина которого равна приведенной длине физического маятника Момент инерции маятника относительно оси вращения проходящей через точку О по теореме Гюйгенса-Штейнера
Отсюда следует, что приведенная длина физического маятника Точка подвеса О и центр качания О´ являются взаимными или сопряженными точками. Это означает, что если маятник подвесить за центр качания О´, то его период не изменится, а прежняя точка подвеса О станет новым центром качания. Это утверждение называется теоремой Гюйгенса. Для ее доказательства обозначим длину отрезка О´С через
Так как приведенная длина равна
то из (2.12) следует, что
то есть приведенная длина, а с ней и период колебаний физического маятника остались без изменений, что доказывает теорему Гюйгенса.
ОПИСАНИЕ УСТАНОВКИ
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Задание 1. Изучение не изохронных колебаний физического и математического маятников. Оборудование и принадлежности: установка с физическим и математическим маятниками, линейка, транспортир. Как следует из теории (п.2.2, 2.3), период колебаний физического маятника зависит от угловой амплитуды колебаний КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Дать определение физических величин: момент силы, момент инерции. 2. Что такое колебание? 3. Дайте определение периода колебаний. 4. Дайте определение частоты колебаний. 5. Какие колебания называются гармоническими? Привести примеры. 6. Запишите закон движения системы, совершающей гармонические колебания. 7. Дайте определение амплитуды гармонических колебаний. 8. Дайте определение фазы гармонических колебаний. 9. Дайте определение начальной фазы гармонических колебаний. 10. Напишите уравнение связи частоты и периода гармонических колебаний. 11. Напишите уравнение связи частоты и циклической частоты гармонических колебаний. 12. Напишите формулу зависимости скорости МТ от времени при гармонических колебаниях. 13. Напишите уравнения связи амплитуды скорости и амплитуды смещения при гармонических колебаниях МТ. 14. Напишите формулу зависимости ускорения МТ от времени при гармонических колебаниях. 15. Напишите уравнения связи амплитуды скорости и амплитуды ускорения при гармонических колебаниях МТ. 16. Напишите уравнения связи амплитуды смещения и амплитуды ускорения при гармонических колебаниях МТ. 17. Напишите дифференциальное уравнение свободных гармонических колебаний МТ. 18. Напишите дифференциальное уравнение свободных затухающих колебаний МТ. 19. Что определяет коэффициент затухания? Добротность? 20. Дайте определение математического маятника. 21. Вывести формулы для периода гармонических колебаний физического (математического) маятников. 22. Что такое центр качания, как он расположен по отношению к точке подвеса? 23. Как определить положение центра масс физического маятника, если известно положение сопряженных точек подвеса при наименьшем периоде колебаний маятника? 24. Почему угловая амплитуда колебаний маятника при измерениях его периода должна быть небольшой? 25. Как влияет трение в системе на точность определения ускорения свободного падения?
ЛИТЕРАТУРА 1. Кембровский Г.С. Приближённые вычисления и методы обработки результатов измерений в физике. -Минск: Изд-во "Университетское", 1990. -189 с. 2. Матвеев А.Н. Механика и теория относительности. -М.: Высшая школа, 1986. -320 с. 3. Петровский И.И. Механика. -Минск: Изд-во БГУ, 1973. -352 с. 4. Савельев И.В. Курс общей физики. -М.: Наука, 1982. Т. 1. Механика. Молекулярная физика. -432 с. 5. Сивухин Д.В. Общий курс физики. М.: Наука, 1989 Т. 1. Механика. -576 с. 6. Стрелков С.П. Механика. -М.: Наука, 1975. -560 с. 7. Физический практикум. Под ред. Кембровского Г.С. -Минск: Изд-во "Университетское", 1986. -352 с.
ПРИЛОЖЕНИЕ 1. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ В экспериментальных исследованиях линейные функциональные зависимости встречаются довольно часто. Примерами могут служить зависимости: силы упругости от деформации (закон Гука Fу = - kx), силы тока в проводнике от напряжения (закон Ома I = U/R), кинетической энергии фотоэлектронов от частоты падающего излучения (закон Эйнштейна E = hn - A) и др. Кроме того, с помощью замены переменных практически любую зависимость можно свести к линейной зависимости вида y = ax + b, (1) где a и b - некоторые подлежащие определению параметры. В частном случае параметр b может быть равен нулю (величины y и x прямо пропорциональны друг другу). Тогда соотношение (1) примет вид y = ax (2) В обоих случаях при обработке результатов измерений можно использовать простой и наглядный графический метод (см. [1], гл. 6). Однако он не отличается высокой точностью, что связано с дополнительными погрешностями при нанесении точек, проведении прямой “на глаз” и снятии отсчетов с графика. Точность можно повысить, если результаты измерений обработать аналитически, используя метод наименьших квадратов. Рассмотрим его применение для простой зависимости (2). Общий случай рассмотрен в [1], § 38.
Пусть некоторая величина y прямо пропорциональна величине х, т.е. y = ax. Экспериментально независимыми способами измерен ряд значений xi, i = 1, 2,..., n, одной величины и соответствующие им значения yi другой величины. При графической обработке результатов измерений полученные данные по соответствующим правилам (см. [1], гл. 6) изображаются в виде точек (рис. 1). Дальнейшая задача сводится к подбору такого угла наклона a проводимой прямой, при котором она располагалась бы возможно ближе ко всем точкам и по обе ее стороны оказывалось бы приблизительно равное их количество. Понятно, что выполнение подобной операции “на глаз” не может обеспечить высокую точностью Более точное математическое правило проведения прямой линии заключается в нахождении такого значения параметра а, при котором сумма квадратов отклонений всех экспериментальных точек от линии графика была бы наименьшей. Обычно случайные погрешности в определении аргумента х незначительны (как правило, в ходе эксперимента значения xi задаются и устанавливаются на приборах самим экспериментатором). Поэтому отклонения экспериментальных точек от прямой, т.е. случайные погрешности Dyi, будут равны разностям ординат данных точек и соответствующих точек на прямой (см. рис. 1). Согласно методу наименьших квадратов наилучшей будет та прямая, для которой будет минимальной величина
По условию минимума производная от величины S по параметру a должна быть равна нулю:
Отсюда наилучшее значение
Для оценки абсолютной случайной погрешности измерения вычисляют так называемое стандартное отклонение
При количестве измерений n³ 10 абсолютную случайную погрешность принимают равной Dac = 3 sa, при n = 5 величина Dac = 5 sa. Относительная случайная погрешность ea,c = Dac/a, или в процентах ea,c = Dac/a 100 %. Инструментальные и другие погрешности оценивают так же, как и при косвенных измерениях (см. [1], гл. 5). Если в формуле (13) ввести обозначения: y = L, x = T2/4p2, то получим формулу (2) Приложения 1, в которой a = g. С помощью формул (5) и (6) Приложения 1 найдём <g> и случайную относительную погрешность косвенных измерений ускорения свободного падения. Можно также построить график зависимости L от (T2/4p2), откладывая L по оси ординат, а (T2/4p2) по оси абсцисс. Этот график должен иметь вид прямой линии, проходящей через начало координат, так как
Коэффициент перед (T2/4p2) в правой части этого уравнения равен тангенсу угла наклона прямой к оси абсцисс, tga = g. Определив по графику tga, можно найти среднее значение ускорения свободного падения, <g>. Но МНК даёт более точное значение <g>, чем графический метод.
ПРИЛОЖЕНИЕ 2. ОТЧЕТ
по лабораторной работе___________ по физике номер ______________________________________________________ название ФИО студента__________________________________________ Группа________________________________________________ Работа выполнена______________________________________ Работа зачтена ___________(дата, балл)____________________
Цель работы: _____________________________________________________
Краткая теория Необходимо привести основные определения, законы и вывод рабочих формул.
Экспериментальная часть Каждое задание должно содержать: 1. Схема экспериментальной установки (нарисовать чертеж и написать наименование деталей). 2. Таблицы (состав таблиц и их количество определить самостоятельно в соответствии с порядком выполнения работы). Для всех величин в таблицах должна быть записана соответствующая единица измерения. 3. Графики должны удовлетворять всем требованиям (см. Приложение 3) 4. Вывод по графику (см. Приложение 3). 5. Оценка погрешностей при измерениях. Выводы. ПРИЛОЖЕНИЕ 3. Требования к оформлению графика: § На миллиметровке или листе в клетку, размер графика должен быть не менее ½ тетрадного листа; § На графике оси декартовой системы, на концах осей – стрелки, индексы величин, единицы измерения, 10 N; § На каждой оси – равномерный масштаб (риски через равные промежутки, числа через равное количество рисок); § Под графиком – полное название графиками словами; § На графике – экспериментальные и теоретические точки ярко; § Форма графика соответствует теоретической зависимости (не ломаная).
ОТВЕТ: По результатам измерений и расчетов получено значение ___________________, равное _____ = (___ ± ____) 10 ___ __________ название физ. характеристики символ среднее ошибка степень един.измер
ВЫВОД по ОТВЕТУ: Полученное экспериментально значение величины _________________, полное название словами равное __________________, с точностью до ошибки измерений, число, единица измерения составляющей ________________, совпадает (не совпадает) с табличным число, единица измерения (теоретическим) значением данной величины, равным ________________. число, единица измерения
ЛАБОРАТОРНАЯ РАБОТА
«Свободные колебания механических Систем» Цель работы: Изучить не изохронные колебания физического и математического маятников; Определить ускорение свободного падения методом оборотного и математического маятников.
ЭЛЕМЕНТЫ ТЕОРИИ
1. СВОБОДНЫЕ КОЛЕБАНИЯ Колебательные явления играют важную роль в самых разнообразных явлениях природы и технических устройствах. Рассмотрим колебательные системы с одной степенью свободы. Мгновенное положение колебательной системы с одной степенью свободы может быть определено с помощью какой-либо одной величины Производная по времени от обобщенной координаты называется обобщенной скоростью В случае колебательных систем с малым трением, диссипацией энергии можно пренебречь, и считать, что полная энергия системы сохраняется во времени. Тогда
Решение этого уравнения имеет вид:
Величина Уравнение (1.2) содержит две произвольные постоянные:
2. ТИПОВЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ. Для определения характера движения механической системы нужно, применяя законы динамики или закон сохранения (превращения) энергии, составить уравнение движения системы, и если оно имеет вид (1.1), то данная система является гармоническим осциллятором, колеблющемся по закону (1.2); при этом частота колебаний Пружинный маятник Пружинный маятник представляет собой систему, состоящую из груза массой
Рис. 1. Пружинный маятник.
Получим уравнение незатухающих колебаний (в отсутствие трения в системе) пружинного маятника двумя способами: из законов динамики и из закона сохранения энергии.
Получили дифференциальное уравнение гармонических колебаний
Как видно из формулы (2.1) период колебаний пружинного маятника не зависит от амплитуды колебаний
Математический маятник. Математический маятник представляет собой материальную точку массой Выведем уравнение собственных колебаний математического маятника.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.176.112 (0.015 с.) |

 , которая называется обобщенной координатой. В качестве обобщенной координаты
, которая называется обобщенной координатой. В качестве обобщенной координаты  , угол поворота системы относительно оси вращения и т.д.
, угол поворота системы относительно оси вращения и т.д. . Тогда потенциальная энергия колебательной системы имеет вид
. Тогда потенциальная энергия колебательной системы имеет вид  , кинетическая энергия выражается формулой
, кинетическая энергия выражается формулой  . Общая энергия колебательной системы
. Общая энергия колебательной системы  в общем случае уменьшается вследствие постепенного расходования доли полной энергии на преодоление сил трения, и свободные колебания реальных колебательных систем являются затухающими.
в общем случае уменьшается вследствие постепенного расходования доли полной энергии на преодоление сил трения, и свободные колебания реальных колебательных систем являются затухающими. , что приводит к дифференциальному уравнению свободных незатухающих колебаний (собственных колебаний):
, что приводит к дифференциальному уравнению свободных незатухающих колебаний (собственных колебаний):

 дает максимальное значение обобщенной координаты и называется амплитудой колебаний. Величина
дает максимальное значение обобщенной координаты и называется амплитудой колебаний. Величина  называется частотой собственных колебаний, величина
называется частотой собственных колебаний, величина 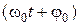 - фазой колебания,
- фазой колебания,  - начальной фазой. Через промежутки времени, кратные
- начальной фазой. Через промежутки времени, кратные  колебательная система возвращается в начальное состояние, и движение системы повторяется. Промежуток времени
колебательная система возвращается в начальное состояние, и движение системы повторяется. Промежуток времени  , прикрепленного к невесомой пружине жесткостью
, прикрепленного к невесомой пружине жесткостью  , которая была выведена из положения равновесия и затем предоставлена самой себе (рис. 1). Груз может совершать колебания как в вертикальной плоскости, так и в горизонтальной, уравнение свободных колебаний в любом из этих случаев будет иметь одинаковый вид, а следовательно, и одинаковое решение.
, которая была выведена из положения равновесия и затем предоставлена самой себе (рис. 1). Груз может совершать колебания как в вертикальной плоскости, так и в горизонтальной, уравнение свободных колебаний в любом из этих случаев будет иметь одинаковый вид, а следовательно, и одинаковое решение.

 . По определению ускорения
. По определению ускорения 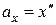 . Сила упругости по закону Гука
. Сила упругости по закону Гука 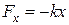 . Тогда
. Тогда  .
Уравнение движения имеет вид (1.1)
.
Уравнение движения имеет вид (1.1)  , где смысл обобщенной координаты
, где смысл обобщенной координаты  имеет деформация пружины
имеет деформация пружины  . Здесь
. Здесь  - длина деформированной пружины,
- длина деформированной пружины,  - длина недеформированной пружины.
- длина недеформированной пружины.
 . Производная по времени от полной энергии равна нулю
. Производная по времени от полной энергии равна нулю  . По определению скорости
. По определению скорости  , тогда
, тогда  или
или  .
.
 по закону
по закону  . Период колебаний равен
. Период колебаний равен (2.1)
(2.1) . Это свойство называется изохронностью колебаний. Однако изохронность имеет место до тех пор, пока справедлив закон Гука. При больших растяжениях закон Гука нарушается, и колебания перестают быть изохронными.
. Это свойство называется изохронностью колебаний. Однако изохронность имеет место до тех пор, пока справедлив закон Гука. При больших растяжениях закон Гука нарушается, и колебания перестают быть изохронными. . По определению углового ускорения
. По определению углового ускорения  . Момент силы тяжести относительно оси вращения, проходящей через точку подвеса О перпендикулярно плоскости колебаний, равен
. Момент силы тяжести относительно оси вращения, проходящей через точку подвеса О перпендикулярно плоскости колебаний, равен 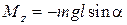 . Тогда
. Тогда  . Для малых углов отклонения
. Для малых углов отклонения  . Момент инерции материальной точки
. Момент инерции материальной точки  , тогда получим
, тогда получим  .
.
 . Производная по времени от полной энергии равна нулю
. Производная по времени от полной энергии равна нулю  , угловая скорость вращения
, угловая скорость вращения  ,
,  , для малых углов отклонения маятника
, для малых углов отклонения маятника  , тогда
, тогда  и
и  .
Отсюда
.
Отсюда 
 .
Математический маятник будет совершать гармонические колебания с частотой
.
Математический маятник будет совершать гармонические колебания с частотой  по закону
по закону  .
Период колебаний равен
.
Период колебаний равен
 (2.2)
(2.2)

 . Тогда
. Тогда  . Здесь I – момент инерции маятника относительно оси колебаний,
. Здесь I – момент инерции маятника относительно оси колебаний,  . Производная по времени от полной энергии равна нулю
. Производная по времени от полной энергии равна нулю  ,
,  .
Отсюда
.
Отсюда  (2.3)
(2.3) , то уравнение (2.3.) можно записать в виде
, то уравнение (2.3.) можно записать в виде  . Исключая из двух последних уравнений время, получим
. Исключая из двух последних уравнений время, получим  или
или (2.4)
(2.4) , где
, где  - максимальный угол отклонения маятника (угловая амплитуда колебаний), придем к закону сохранения энергии:
- максимальный угол отклонения маятника (угловая амплитуда колебаний), придем к закону сохранения энергии: (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) есть учетверенное время прохождения интервала углов от
есть учетверенное время прохождения интервала углов от  до
до  , получим для периода колебаний физического маятника выражение
, получим для периода колебаний физического маятника выражение (2.8)
(2.8) (2.9)
(2.9) , а период колебаний выражается формулой:
, а период колебаний выражается формулой: (2.10)
(2.10) , (2.11)
, (2.11) . Точка О´ называется центром качания. Центр качания можно определить как математическую точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений.
. Точка О´ называется центром качания. Центр качания можно определить как математическую точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений. , где
, где  - момент инерции маятника относительно параллельной оси, проходящей через центр масс С. Тогда приведенная длина физического маятника примет вид:
- момент инерции маятника относительно параллельной оси, проходящей через центр масс С. Тогда приведенная длина физического маятника примет вид: (2.12)
(2.12) , то есть точка подвеса О и центр качания О´ лежат по разные стороны от центра масс С. Во-вторых, всем точкам подвеса, одинаково удаленным от центра масс маятника, соответствует одна и та же приведенная длина, а следовательно, один и тот же период колебаний.
, то есть точка подвеса О и центр качания О´ лежат по разные стороны от центра масс С. Во-вторых, всем точкам подвеса, одинаково удаленным от центра масс маятника, соответствует одна и та же приведенная длина, а следовательно, один и тот же период колебаний. (рис.3) и допустим, что маятник подвешен за точку О´. Тогда его приведенная длина будет равна:
(рис.3) и допустим, что маятник подвешен за точку О´. Тогда его приведенная длина будет равна: (2.13)
(2.13) (2.14)
(2.14) . Подставляя последнее выражение в (2.14) получим:
. Подставляя последнее выражение в (2.14) получим: или
или  ,
,

 необходимо измерить угловую амплитуду колебаний маятника и его период, и полученные данные представить в виде графика.
необходимо измерить угловую амплитуду колебаний маятника и его период, и полученные данные представить в виде графика. Рис. 1
Рис. 1
 (3)
(3) (4)
(4) (5)
(5) (6)
(6)



