
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение внутренних усилий в рамах методом перемещений и их проверка. Алгоритм расчета.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
На основании принципа суперпозиции достаточно «собрать» результаты отдельных частных расчетов. Таким образом, значения изгибающих моментов в заданной системе получаются по зависимости:
где Изгибающие моменты в заданной системе, вычисленные по формуле (9.10), часто называют окончательными. В отличие от них, моменты, найденные ранее в основной системе, считаются промежуточными или вспомогательными. Единичные эпюры, умноженные на соответствующие значения Z1; Z2,..., Zn, иногда называют «исправленными» эпюрами. Определение поперечных и продольных сил. При расчете рам и балок поперечные силы Q вычисляют по значениям изгибающих моментов M, а продольные силы N - по значениям поперечных сил. Для плоских рам удобно использовать следующие приемы. Поперечные силы Q могут быть найдены по значениям изгибающих моментов M. Если эпюра M на участке стержневой системы прямолинейна, удобно пользоваться дифференциальной зависимостью при изгибе
По этой зависимости, поперечная сила равна тангенсу угла наклона прямолинейной эпюры моментов. Правило знаков следующее: сила Q считается положительной, если для совмещения оси стержня с эпюрой М ось необходимо вращать по часовой стрелке (рисунок 7.10).
Если эпюра M на участке непрямолинейна, поперечную силу удобно находить, вырезая участок и составляя для него уравнения равновесия. Пусть, например, для рамы построена эпюра изгибающих моментов (рисунок 7.11, а). Чтобы найти поперечные силы на участке АВ, вырежем его и приложим к сечениям известные моменты и пока неизвестные силы (рисунок 7.11, б). Моменты направляем так, как следует из эпюры изгибающих моментов М: эпюра построена на растянутых волокнах, значит, в сечениях А и В растянуты верхние волокна. Поперечные силы считаем положительными, т. е. они вращают рассматриваемый участок по часовой стрелке.
Составим уравнения моментов относительно точек А и В
По полученным значениям строим эпюру Q (см. рисунок 7.11, б). В сечении с абсциссой где Q = 0, изгибающий момент экстремален. Чтобы его найти, вырезаем участок длиной z0 (рисунок 7.11, в), из уравнения проекций на вертикальную ось Qa - qz0 = 0 определяем z0 = QA / q. Экстремальный момент находим из уравнения
Продольные силы N могут быть найдены по значениям поперечных сил Q. Для этого необходимо отсечь отдельные стержни или вырезать узлы рамы, составить уравнения проекций на оси координат, из которых выразить искомые усилия. Проверки правильности определения внутренних усилий. В методе сил проверкой правильности определения внутренних сил было соблюдение условий совместности деформаций в заданной системе (деформационная, или кинематическая проверка). В методе перемещений, напротив, эти условия автоматически выполняются при любых перемещениях узлов Zx, Z2,..., Zn. Критерием правильности решения задачи является, очевидно, то, что внутренние усилия, вычисленные по данным перемещениям, удовлетворяют и всем условиям равновесия системы (статическая проверка). Фактически надо убедиться, что в условно введенных связях основной системы полные реакции равны нулю, т. е.
Для этого надо вырезать узлы и части конструкции и проверить, находятся ли они в равновесии под действием только внутренних усилий, приложенных в местах разрезов. Проверка эпюры изгибающих моментов вычислением реакций связей. В п. 9.4.2 была получена формула (9.6) для определения реакции i-ой дополнительной связи, предполагающая перемножение эпюр
Суммируя все грузовые реакции, получим
Условие (9.11) является необходимым и при верно построенных исходных единичных и грузовой эпюрах достаточным условием правильности эпюры М. Порядок расчета рам методом перемещений. Расчет статически неопределимых рам, а также балок, работающих на изгиб, удобно вести в следующем порядке: 1) вычисление степени кинематической неопределимости nK; 2) формирование основной системы; 3) составление системы канонических уравнений; 4) построение единичных и грузовой эпюр в основной системе; 5) вычисление единичных и грузовых реакций и их проверка; 6) решение системы канонических уравнений; 7) построение эпюры изгибающих моментов М и ее проверки; 8) построение эпюры поперечных сил Q (по готовой эпюре М); 9) построение эпюры продольных сил N (по готовой эпюре Q); 10) статическая проверка равновесия рамы в целом. 17.Расчет рам методом перемещений на изменение температуры (канонические уравнения при температурном воздействии, определение «температурных» реакций, определение внутренних усилий и их проверка). Как известно, неравномерный нагрев волокон каждого из элементов системы проиводит к изменению длин и искревлению в рез-те чего возникают внутренние усилия. Общий расчет на температурное воздействие тот же, сто и при силовом: 1)основная система формируется введением дополнительных связей. 2)канонические уравнения имеют вид
……………… Т.е вместо грузовых реакций, канонические уравнения содержат температурные реакции Решаем задачу по методу сил
«-«По тому что эпюра находится со стороны более холодных волокон. Кроме изгиба температурное воздействие вызывает удлинение стержней на
Где Замечание: если вместо опорного стержня на торце находится шарнир, то удлинение от действия температуры не происходит. При этом в правой опоре возникает гор. реакция
Рассмотрим расчет о.с м.п. при температурном воздействии: По принципу суперпозиции можно раздельно рассматривать равномерный и неравномерный нагрев элемента. Данная рамма имеет один жесткий узел.
1) Равномерный нагрев.
Пусть элементы нагреваются на Плавающая заделка сместилась линейно. Стержени изогнулись. В этом случай эпюру изгиб. Моментов можно построить по табл.,используя результаты для ед. смещения и умножая их на реальные смещения узлов.
2) Неравномерный нагрев Эпюру для каждого участка строим по табл
Далее рассматриваем равновесие узла при равномер. И неравномер. Нагреве определяем
По принципу суперпозиции находим Каноничекое уравнение
Z1 определяем из каноничесого уравнения
Окончательная эпюра моментов строится как и при силовом воздействии, только Мр–Мt0 и M Q- по эпюре М N- по эпюре Q Делаем деф. проверку
18.Расчет рам методом перемещений на смещение опор (канонические уравнения метода перемещений при кинематическом воздействии, определение реакций в основной системе от кинематического воздействия, определение внутренних усилий и их проверка). Смещение опорных связей вызывает изгиб элементов и следовательно возникновение внутренних усилий Порядок расчета вцелом остается прежним как и при силовом воздействии 1 опр.ст. кинем неопредел. 2 формируем осн.сист. 3 сосот. Систему канонич.ур-ний
Основная система
Где 4 ед.эпюры в осн.системе. и определение единичных реакций 5 исследование воздействия угловыхсмещений опорных связей,построение эпюры Задаем смещение заделок на углы φ1 и φ2
Сост φ о.с.
Строим эпюру по таблице приложения, умножаем данные от единичных углов поворота на значение реальных смещений
При определении реакций вырезаем узлы рамы состояния φ и рассм. их равновесие
6 исследование линейных смещений опорных связей (сост δ) построение ипюры Мδ и определ
сост δ
7 решаем систему канонических уравнений Z1,Z2,Z3 8 построение эпюры изгибающих моментов M= 9 проверка эпюры моментов
Где МΣ – суммарная единичная эпюра 10 построение эпюры Q по M 11 построение эпюры N по Q 12 статическая проверка равновесмя рамы 19 Расчет неразрезных балок методом перемещений (рекомендации по формированию основной системы, канонические уравнения) Основная система ее формирование: Основная система получается введением плавающих заделок в узлы которым придаются углы поворота Z1, Z2. Очевидно что при отбрасывании консоли количество неизвестных будет меньше. Порядок расчета:
где
2. Выбор основной системы. Для неразрезной балки основная система получается введением заделок над опорами (рис. 1.1, в). За неизвестные принимаются углы поворотов сечений балки над опорами 3. Канонические уравнения метода перемещений. Для трижды кинематически неопределимой балки, канонические уравнения метода перемещений имеют вид:
где 4. Определение коэффициентов канонических уравнений. Для определения коэффициентов необходимо построить единичные и грузовые эпюры, используя таблицы реакций. Для нахождения коэффициентов можно применить два способа: а) статический способ; б) способ перемножения эпюр. По статическому способу единичные коэффициенты и свободные члены, представляющие реактивные моменты во введенных заделках, определяются из условий равновесия вырезаемых из основной системы узлов в виде По второму способу коэффициенты при неизвестных определяются путем интегрирования (перемножения) соответствующих эпюр:
где Свободные члены канонических уравнений определяются по формуле:
где 5. Решение системы канонических уравнений. Найденные коэффициенты при неизвестных и свободные (грузовые) члены подставляются в канонические уравнения, решение которых дает значения неизвестных перемещений 6. Построение расчетной эпюры изгибающих моментов. Расчетная эпюра изгибающих моментов строится по формуле:
где Для контроля расчетной эпюры изгибающих моментов служат: а) статическая проверка, которая заключается в проверке условий равновесия узлов системы. б) деформационная проверка
где 7. Построение эпюры поперечных сил. Эпюра поперечных сил Q строится по расчетной эпюре изгибающих моментов (1.6). Для контроля производится статическая проверка.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1033; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.109 (0.01 с.) |

 (9.10)
(9.10) k, Mp - изгибающие моменты в основной системе от единичного перемещения k-ой дополнительной связи и от внешней нагрузки соответственно.
k, Mp - изгибающие моменты в основной системе от единичного перемещения k-ой дополнительной связи и от внешней нагрузки соответственно.



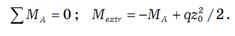

 . Здесь под Mр
. Здесь под Mр 
 (9.11)
(9.11)

 …..
…..  . Для того чтобы их найти, отдельно рассматривают статически неопределимые стержни, неравномерно нагретые сверху и снизу.
. Для того чтобы их найти, отдельно рассматривают статически неопределимые стержни, неравномерно нагретые сверху и снизу. 


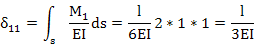
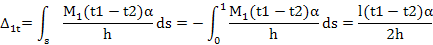

 -приращение температуры на уровне центра тяжести сечения.
-приращение температуры на уровне центра тяжести сечения. . Которую необходимо учитывать в расчетах.
. Которую необходимо учитывать в расчетах.





 , в результате они удлинились. Для симметричного сечения
, в результате они удлинились. Для симметричного сечения 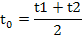


 и
и  .
.
 =
= 
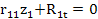

 t
t

 Для удобства перемещения как заданные(С1,С2,φ) так и неизвестные (Z1,Z2) изображае в виде стрелок с указанием направлений
Для удобства перемещения как заданные(С1,С2,φ) так и неизвестные (Z1,Z2) изображае в виде стрелок с указанием направлений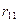
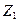 +
+ 
 +
+ 
 +
+  =0
=0


 =0
=0

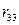
 =0
=0 -реакция i-ой связи от заданных смещений опор. Эти реакции удобно определять как сумму 2-х составляющих
-реакция i-ой связи от заданных смещений опор. Эти реакции удобно определять как сумму 2-х составляющих  =
=  +
+  где
где 





 по таблицам с учетом заданных линейных смещений, умножая табличные данные на величины поперечных смещений узлов каждого стержня
по таблицам с учетом заданных линейных смещений, умножая табличные данные на величины поперечных смещений узлов каждого стержня


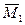 *Z1+
*Z1+  *Z2+
*Z2+  * Z3+ Мδ+ Мφ
* Z3+ Мδ+ Мφ
 , (1.11)
, (1.11) – число неизвестных углов поворота, равное числу «жестких» узлов расчетной схемы.
– число неизвестных углов поворота, равное числу «жестких» узлов расчетной схемы. – число независимых линейных перемещений узлов расчетной схемы (для неразрезных балок
– число независимых линейных перемещений узлов расчетной схемы (для неразрезных балок  .
.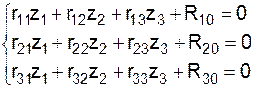 , (1.12)
, (1.12) – значение единичного коэффициента;
– значение единичного коэффициента;  – значение грузового коэффициента;
– значение грузового коэффициента;  – значение неизвестного перемещения.
– значение неизвестного перемещения. .
. , (1.13)
, (1.13) – эпюры от единичных перемещений введенных связей, построенные в основной системе метода перемещений.
– эпюры от единичных перемещений введенных связей, построенные в основной системе метода перемещений. , (1.14)
, (1.14) – эпюра изгибающих моментов от внешней нагрузки, построенная в любой статически определимой системе, образованной из заданной (т. е. в основной системе метода сил).
– эпюра изгибающих моментов от внешней нагрузки, построенная в любой статически определимой системе, образованной из заданной (т. е. в основной системе метода сил).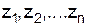 .
. , (1.15)
, (1.15) – эпюра изгибающих моментов в основной системе метода перемещений от нагрузки;
– эпюра изгибающих моментов в основной системе метода перемещений от нагрузки;  – эпюры изгибающих моментов в основной системе метода перемещений от единичных перемещений введенных связей;
– эпюры изгибающих моментов в основной системе метода перемещений от единичных перемещений введенных связей;  – найденные значения перемещений узлов.
– найденные значения перемещений узлов. , (1.16)
, (1.16) – эпюра изгибающих моментов, построенная в основной системе метода сил от действия любого i-гонеизвестного метода сил (или суммарной единичной эпюры метода сил).
– эпюра изгибающих моментов, построенная в основной системе метода сил от действия любого i-гонеизвестного метода сил (или суммарной единичной эпюры метода сил).


