Вычисление коэффициентов и свободных членов канонических уравнений статическим методом.

Существует два метода нахождения единичных и грузовых ре­акций: статический и общий (кинематический).

Статический метод определения реакций. Так как коэф­фициенты и свободные члены канонических уравнений есть ре­акции связей основной системы - силы и моменты, то они могут быть определены из уравнений статического равновесия узлов и отдельных частей конструкции.

Если Z₁ - угол поворота (см. рисунок 9.8), то связь 1 - пла­вающая заделка, а реакции этой связи г₁₁, г₁₂,..., r_1n, R_1p - мо­менты; если Z₂ - горизонтальное перемещение, то связь 2 - го­ризонтальный стержень, а реакции этой связи r₂₁, r₂₂,..., r_2n, R_2p - горизонтальные силы.

Для определения моментнои реакции необходимо вырезать узел основной системы и рассмотреть его равновесие, составив уравнение в виде суммы моментов сил, приложенных к узлу (ри­сунок 9.9, а).

Чтобы найти силовую реакцию, следует отсечь часть основной системы, содержащую эту реакцию, и составить уравнение ее равновесия в виде суммы проекций всех сил на какую-либо ось (рисунок 9.9, б).

 

Предварительно необходимо построить эпюры в основной сис­теме от единичных перемещений (в единичных состояниях) и за­данной внешней нагрузки (в грузовом состоянии), пользуясь вспомогательными таблицами (см. Приложение).

Направление определяемых единичных и грузовых реакций всегда совпадает с направлением перемещения данной связи. На­пример, реакции r₁₁, r₁₂,..., r_1n, R_1p необходимо направить в ту же сторону, что и Z₁.

Статический метод прост, нагляден и удобен, он позволяет изобразить каждую реакцию на расчетной схеме в виде силы или момента и таким образом избежать ошибок при расчете. Однако в некоторых случаях он неприменим.

Например, для рамы с наклонными стойками в уравнения проекций на оси координат войдут не только поперечные, но и продольные силы (рисунок 9.10). Попе­речные силы легко найти по таблицам, однако продольные при использовании допущения об абсолютной жесткости стержней определить гораздо сложнее.

В случаях, когда составление уравне­ний равновесия громоздко, для определе ния реакций используют общий метод, основанный на перемножении эпюр.

 

 

 

 

Вычисление коэффициентов и свободных членов канонических уравнений общим (кинематическим) методом.

Единичные перемещения δ_ik вычисляются пере­множением единичных эпюр M_i и M_k, грузовые ∆_iр - перемноже­нием эпюр Mi и M_p в основной системе метода сил.

Подобным же образом можно найти единичные и грузовые ре­акции в основной системе метода перемещений, однако здесь есть свои особенности.

Единичные реакции можно найти перемножением соответст­вующих единичных эпюр в основной системе:

(9.5)

Из формулы (9.5) следует, что главные коэффициенты rii все­гда положительны, а побочные коэффициенты rik (i k) могут иметь любой знак; в частности, они могут оказаться нулевыми.

Грузовые реакции. На первый взгляд, по аналогии с (9.5) гру­зовую реакцию Rip можно вычислить перемножением эпюр Mi и Mp в основной системе. Но эта аналогия оказывается ложной, так как результат перемножения этих эпюр равен нулю:

Можно доказать, что

(9.6)

где Mр - эпюра изгибающих моментов от внешней нагрузки, построенная в любой системе, не содержащей i-ой дополнительной связи (как правило, в статически определимой, образованной из заданной отбрасыванием лишних связей).

Проверка коэффициентов и свободных членов канонических уравнений метода перемещений (единичных и грузовых реакций).

Формулы (9.5), (9.6) позволяют выполнить проверку правильности вычис­ления единичных и грузовых реакций.

Предварительно необходимо построить суммарную единичную эпюру Σ, сложив все единичные эпюры в основной системе:

(9.7)

Универсальная проверка. Результат умножения суммарной единичной эпюры (9.7) самой на себя должен быть равен алгеб­раической сумме всех единичных реакций. Докажем это:

(9.8)

Постолбцовая проверка. Правильность определения свобод­ных членов канонических

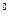уравнений - грузовых реакций - про­веряют, умножая эпюру Σ на эпюруMр от внешней нагрузки, построенную в статически определимой системе:

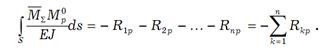(9.9)