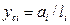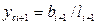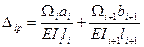Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет бесшарнирной арки на неподвижную нагрузку (общий ход расчета, особенности расчета с ос, полученной разрезанием арки по оси симметрии).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
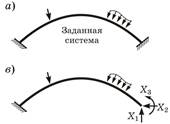
Бесшарнирная арка (рис, а) три раза статически неопределима (nc = 3). ОС метода сил получается удалением трех избыточных связей, например, введением трех шарниров (рис, б), отбрасыванием жесткой опоры (рис, б); разрезанием арки по оси симметрии (рис, г) и добавлением неизвестных реакций этих связей X1, X2, X3. Для симметричной арки желательно выбирать и симметричную ОС. В этом случае многие расчеты можно будет производить только для половины арки. КУ выражают условия отсутствия перемещений по направлениям неизвестных усилий X1, X2, X3. В первом случае это углы поворота опорных сечений и взаимный угол поворота сечений в замке; во втором - линейные и угловое перемещения конца консоли. Для ОС на рис, г КУ (1) выражают условие полной взаимной неподвижности левого и правого сечений в месте разреза. В общем случае КУ: δ11X1+δ12Х2+δ13Х3+∆1p=0; δ21X1+δ22X2+δ23Х3+∆2Р=0; (1) δ31X1+δ32Х2+δ33Х3+∆3р=0. Входящие в них перемещения определяются по методу Мора:
где Наиболее простой расчет получится с использованием основной системы, показанной на рис, г, так как четыре из побочных коэффициентов будут нулевыми: δ12=δ21=δ23=δ32=0. После решения КУ вычисляются значения внутр. усилий M, N, Q по ф-лам: M = N = Q = Далее необходимо выполнить кин. (деф.) проверку правильности вычисления внутр. усилий. Для этого можно использовать усилия одного из ед. состояний Здесь ∆i - перемещение по направлению Xi. Выполнение условий (8.13) и (8.14) говорит о том, что перемещения по направлениям реакций отброшенных связей отсутствуют, что соответствует расчетной схеме заданной бесшарнирной арки. 5. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ФЕРМ (СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ ПЛОСКИХ ФЕРМ, ОБЩИЙ ХОД РАСЧЕТА, ОСОБЕННОСТИ ВЫЧИСЛЕНИЯ ПЕРЕМЕЩЕНИЙ). Степень статической неопределимости (кол-во лишних стержней): nc = С0 - 2У, где У - количество узлов фермы (шарниров), непосредственно не связанных с землей; С0 - количество одиночных связей (стержней фермы и опорных стержней).
Избыточными (лишними) могут быть как связи опор, так и элементы самой фермы. Внешне статически неопределимая ферма содержит лишние опорные стержни, но сама она, отделенная от опор, статически определима. Внутренне статически неопределимая ферма имеет минимально необходимое количество опорных связей, однако в ее структуре присутствуют больше стержней, чем нужно для неизменяемости
Общий ход расчета. ОC метода сил образуется разрезанием стержней фермы либо устранением избыточных опорных связей. ОС, получаемая разрезанием стержней фермы, во многих случаях оказывается удобнее ОС, в которой устраняются опорные связи. В общем случае КУ имеют стандартный вид. Для n раз статически неопределимой фермы:
δ ki = После решения КУ вычисляются значения продольных сил в ферме по формуле: N (j) = Далее следует выполнить статическую проверку правильности вычисления внутренних усилий, вырезав несколько узлов и проверив их равновесие. Для кинематической (деформационной) проверки необходимо взять усилия одного из единичных состояний (k = 1, 2,..., n) ∆ k =
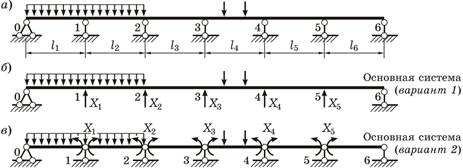
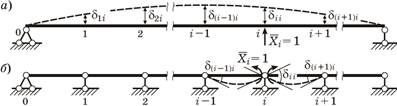
6.ОБЩИЕ СВЕДЕНИЯ О НЕРАЗРЕЗНЫХ БАЛКАХ. СТЕПЕНЬ СТАТИЧЕСКОЙ НЕОПРЕДЕЛИМОСТИ. ВЫБОР ОСНОВНОЙ СИСТЕМЫ МЕТОДА СИЛ. Неразрезной наз. статически неопределимая сплошная балка, имеющая более двух опор и, следовательно, перекрывающая более одного пролета(рис, а). Характерным ее отличаем от многопролетной балки (рис, б) явл. то, что нагрузка, приложенная в любом пролете, изгибает неразрезную балку на протяжении всех ее пролетов, создавая плавную упругую линию. Типы неразрезных балок: простая неразрезная - если балка своими концами опирается на шарнирные опоры; консолъно-неразрезная - если имеет консоли; неразрезная балка с защемлениями - если ее концы закреплены жесткой и скользящей заделками Характерным ее отличием от многопролетной шарнирной балки (рис, б) является то, что нагрузка, приложенная в любом пролете, изгибает неразрезную балку на протяжении всех ее пролетов, создавая плавную упругую линию. Типы неразрезных балок: простая неразрезная - если балка своими концами опирается на шарнирные опоры; консолъно-неразрезная - если имеет консоли; неразрезная балка с защемлениями - если ее концы закреплены жесткой и скользящей заделками
Нетрудно убедиться, что для первого варианта ОС любая сила Xi = 1 вызывает перемещения по направлениям всех неизвестных сил (рис, а). Для второго варианта ОС любой момент Xi = 1 деформирует только два смежных пролета по обе стороны от опоры, где он приложен, и вызывает перемещения только по направлениям трех неизвестных: Xi-1, Xi и Xi+1 (рис, б). Следовательно, в первой ОС каждое побочное перемещение δ ij (i≠j) не равно нулю, и КУ будут полными. Во второй ОС большое число побочных коэффициентов будет =0, КУ упростятся. Следовательно, вторая ОС рациональнее первой, она и будет рассматриваться далее.
Заметим, что при малом числе промежуточных опор (1-2) может применяться и первый вариант ОС. Уравнение трех моментов Вывод уравнения трех моментов. Положим, что балка имеет ступенчато переменное сечение с постоянным моментом инерции Ji в каждом i-м пролете. Рассмотрим два смежных пролета выбранного варианта основной системы, i-й и (i + 1)-й (рисунок 8.15, а). Запишем i-ое каноническое уравнение метода сил:
Очевидно, что моменты X1, X2, Xi -2 и Xi+ 2,..., Xn не деформируют рассматриваемые пролеты балки и, следовательно, не вызывают перемещений по направлению момента Xi. Поэтому коэффициенты При определении перемещений по методу Мора будем учитывать только изгибающие моменты, пренебрегая поперечными силами. Перемножая эпюры по правилу для прямолинейных эпюр на участке постоянной жесткости, получаем:
Подставим в уравнение (8.21):
Умножая его на произвольное значение 6EJ0, получим:
где Каноническое уравнение метода сил, записанное в форме (8.23), называется уравнением трех моментов. Оно связывает три последовательных неизвестных опорных момента для двух смежных пролетов с длинами li и li + 1. Смысл i-го уравнения: отсутствие взаимного угла поворота сечений балки на i-ой опоре. Подчеркнем, что 6EJ0 - произвольная величина. Однако для удобства в качестве J0 принимают момент инерции одного из пролетов балки. Тогда приведенные и реальные длины пролетов имеют одинаковую размерность.
8. Формула для грузового перемещения. Построим грузовую эпюру Mp (рисунок 8.15, д) и перемножим ее с эпюрой Mi (см. рисунок 8.15, в) по правилу Верещагина:
где Рассматривая подобные треугольники эпюры Mi, получаем:
С учетом этого формула для грузового перемещения принимает вид:
где a, b - расстояния от центра тяжести эпюры Mp до левой и правой опор.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 564; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.007 с.) |



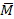 i ,
i , 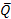 i ,
i ,  i и Mp, Qp, Np - внутренние усилия в ОС от Xi = 1 и внешней нагрузки соответственно; S - длина оси арки; ds - бесконечно малый элемент оси; EJ, GA, EA - жесткости сечения соответственно при изгибе, сдвиге и растяжении- сжатии; η- коэф, учитывающий неравномерность распределения кас. напряжений по поперечному сечению при изгибе и зависящий от формы сечения.
i и Mp, Qp, Np - внутренние усилия в ОС от Xi = 1 и внешней нагрузки соответственно; S - длина оси арки; ds - бесконечно малый элемент оси; EJ, GA, EA - жесткости сечения соответственно при изгибе, сдвиге и растяжении- сжатии; η- коэф, учитывающий неравномерность распределения кас. напряжений по поперечному сечению при изгибе и зависящий от формы сечения.


 единичные и грузовые перемещения, входящие в КУ, определяются соотношениями:
единичные и грузовые перемещения, входящие в КУ, определяются соотношениями: ;∆kp=
;∆kp=  где
где  ,
,  -продольная сила в j-ом стержне ОС от ед. силы, приложенной по направлению Xk и внешней нагрузки соответственно; lj, EAj - длина и жесткость j-го стержня. Знак суммы распространяется на все стержни системы.
-продольная сила в j-ом стержне ОС от ед. силы, приложенной по направлению Xk и внешней нагрузки соответственно; lj, EAj - длина и жесткость j-го стержня. Знак суммы распространяется на все стержни системы. , где N (j) - продольная сила в j-ом стержне заданной фермы.
, где N (j) - продольная сила в j-ом стержне заданной фермы.
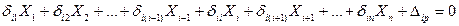

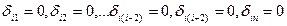 . Уравнение принимает вид:
. Уравнение принимает вид:  (8.21)
(8.21)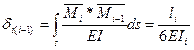



 (8.23)
(8.23)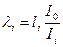 - приведенная длина i-го пролета.
- приведенная длина i-го пролета.

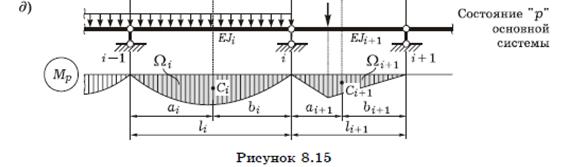
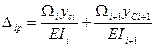
 - площадь эпюры Mp в i-м и (i + 1)-м пролетах; yCi - ордината эпюры Mi под центром тяжести Сi эпюры Mp в i-м пролете; yCi+1 - то же, в (i + 1)-м пролете; EJi, EJi + 1 - жесткости балки в i-м и (i + 1)-м пролетах.
- площадь эпюры Mp в i-м и (i + 1)-м пролетах; yCi - ордината эпюры Mi под центром тяжести Сi эпюры Mp в i-м пролете; yCi+1 - то же, в (i + 1)-м пролете; EJi, EJi + 1 - жесткости балки в i-м и (i + 1)-м пролетах.