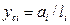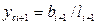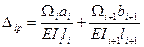Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы статически неопределимых арок. Особенности расчета статически неопределимых арок. Законы изменения сечений арок.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Типы статически неопределимых арок. Особенности расчета статически неопределимых арок. Законы изменения сечений арок.
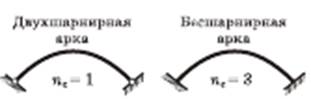
Типы статически неопределимых арок: двухшарнирная и бесшарнирная. Первая из них один раз статически неопределима, так как содержит одну лишнюю связь (nc = 1), вторая – три раза (nc = 3). Если опорные устройства или нижележащие элементы неспособны воспринимать распор, в арках устраиваются затяжки. Затяжка-это стержень, который соединяет элементы конструкции между собой. 
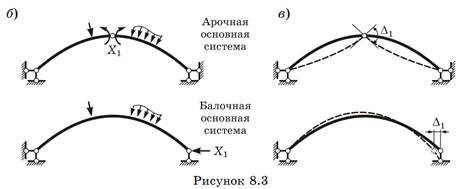
Если опоры не могут воспринимать распор Н,то устанавливается затяжка, работающая на растяжение. Продольная сила в ней N=H. Особенности расчета статически неопределимых арок. 1)В арках внутренние усилия (M, Q, N) и перемещения зависит не только от внешней нагрузки, но и от формы оси, а в статически неопределимых арках – еще и от геометрических характеристик поперечных сечений (площадей A и моментов инерции J.(так как для определения внутренних усилий в статически неопределимых арках методом сил необходимо определять перемещения Δ и δ, содержащие жесткости EI,EA,GA). 2) При расчете перемещений по методу Мора необходимо учитывать для плоской задачи все 3 слагаемых, содержащих М,Q,N. Однако в учебных и предварительных расчетах допускается пренебрегать влиянием на перемещения поперечных, а в некоторых случаях и продольных сил. Интегралы Мора вычисляют приближенно, используя численные методы. Способы «перемножения эпюр» неприменимы, так как все эпюры внутренних усилий в арках криволинейны. В виде исключения можно разбить ось арки на малые участки, в пределах которых и ось, и эпюры считать прямолинейными; «перемножить» эпюры для каждого участка, а результаты просуммировать. Законы изменения сечений арок:Закон изменения площади сечения 2) бесш. Расчет двухшарнирной арки на неподвижную нагрузку (общий ход расчета, особенности расчета арки с балочной основной системой). Заданная двухшарнирная арка (рис. а) содержит одну лишнюю связь, поэтому для получения статически определимой основной системы метода сил необходимо эту связь отбросить и заменить действием реакции X1.
1) Основная система метода сил может быть образована двумя способами (б): в виде трехшарнирной арки (арочная основная система) или криволинейной балки (балочная основная система). В первом случае X1 представляет собой изгибающий момент в замковом сечении, во втором – горизонтальную опорную реакцию (распор).
2) Приравняв это выражение к нулю, получим каноническое уравнение: δ11X1 +Δ1p=0,где δ11 – перемещение по направлению X1, вызванное единичным силовым фактором, приложенным в направлении X1; Δ1p – перемещение по направлению X1 от внешней нагрузки. 3)Затем, воспользовавшись методом Мора, необходимо найти перемещения δ11 и Δ1p:
4) Из уравнения следует, что X =(−Δ p) /δ. 5) Определяем изгибающие моменты, поперечные и продольные силы в за- данной арке: Q = Q1X1 + Qp; N = N1X1 + Np, M=M1X1+Мр 6) Проверка Особенности расчета арки с балочной основной системой
допускается не учитывать поперечные силы при определении δ11, продольные и поперечные силы – при определении Δ1р.
Уравнение трех моментов Вывод уравнения трех моментов. Положим, что балка имеет ступенчато переменное сечение с постоянным моментом инерции Ji в каждом i-м пролете. Рассмотрим два смежных пролета выбранного варианта основной системы, i-й и (i + 1)-й (рисунок 8.15, а). Запишем i-ое каноническое уравнение метода сил:
Очевидно, что моменты X1, X2, Xi -2 и Xi+ 2,..., Xn не деформируют рассматриваемые пролеты балки и, следовательно, не вызывают перемещений по направлению момента Xi. Поэтому коэффициенты При определении перемещений по методу Мора будем учитывать только изгибающие моменты, пренебрегая поперечными силами. Перемножая эпюры по правилу для прямолинейных эпюр на участке постоянной жесткости, получаем:
Подставим в уравнение (8.21):
Умножая его на произвольное значение 6EJ0, получим:
где Каноническое уравнение метода сил, записанное в форме (8.23), называется уравнением трех моментов. Оно связывает три последовательных неизвестных опорных момента для двух смежных пролетов с длинами li и li + 1. Смысл i-го уравнения: отсутствие взаимного угла поворота сечений балки на i-ой опоре. Подчеркнем, что 6EJ0 - произвольная величина. Однако для удобства в качестве J0 принимают момент инерции одного из пролетов балки. Тогда приведенные и реальные длины пролетов имеют одинаковую размерность.
8. Формула для грузового перемещения. Построим грузовую эпюру Mp (рисунок 8.15, д) и перемножим ее с эпюрой Mi (см. рисунок 8.15, в) по правилу Верещагина:
где Рассматривая подобные треугольники эпюры Mi, получаем:
С учетом этого формула для грузового перемещения принимает вид:
где a, b - расстояния от центра тяжести эпюры Mp до левой и правой опор. Рис. 20.12
Для расчета статически неопределимых систем по теории предельного равновесия можно воспользоваться одним из двух способов - кинематическим или статическим. При применении кинематического способа, в предельном состоянии составляется уравнение работы всех внешних и внутренних усилий на основе принципа возможных перемещений. Этот принцип формулируется так: если система твердых тел находится в равновесии под действием системы сил, то работа, совершаемая этими силами на любом малом возможном перемещении системы, должна быть равна нулю. При применении статического способа при отсутствии упругого расчета, на основе которого, предварительно можно определить наиболее вероятную схему разрушения конструкции, задаются различные схемы разрушения предельной стадии работы рассматриваемой системы, и для каждой из них составляются уравнения равновесия и определяются предельные значения внешних сил. Из их числа, наименьшая является расчетной величиной предельной силы. Из числа рассмотренных схем разрушения, на основании которых определяется предельная сила, является наиболее вероятной схемой, разрушения конструкции.
Типы статически неопределимых арок. Особенности расчета статически неопределимых арок. Законы изменения сечений арок.
Типы статически неопределимых арок: двухшарнирная и бесшарнирная. Первая из них один раз статически неопределима, так как содержит одну лишнюю связь (nc = 1), вторая – три раза (nc = 3). Если опорные устройства или нижележащие элементы неспособны воспринимать распор, в арках устраиваются затяжки. Затяжка-это стержень, который соединяет элементы конструкции между собой. 
Если опоры не могут воспринимать распор Н,то устанавливается затяжка, работающая на растяжение. Продольная сила в ней N=H. Особенности расчета статически неопределимых арок. 1)В арках внутренние усилия (M, Q, N) и перемещения зависит не только от внешней нагрузки, но и от формы оси, а в статически неопределимых арках – еще и от геометрических характеристик поперечных сечений (площадей A и моментов инерции J.(так как для определения внутренних усилий в статически неопределимых арках методом сил необходимо определять перемещения Δ и δ, содержащие жесткости EI,EA,GA). 2) При расчете перемещений по методу Мора необходимо учитывать для плоской задачи все 3 слагаемых, содержащих М,Q,N. Однако в учебных и предварительных расчетах допускается пренебрегать влиянием на перемещения поперечных, а в некоторых случаях и продольных сил. Интегралы Мора вычисляют приближенно, используя численные методы. Способы «перемножения эпюр» неприменимы, так как все эпюры внутренних усилий в арках криволинейны. В виде исключения можно разбить ось арки на малые участки, в пределах которых и ось, и эпюры считать прямолинейными; «перемножить» эпюры для каждого участка, а результаты просуммировать. Законы изменения сечений арок:Закон изменения площади сечения 2) бесш.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

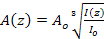 , Законы изменения момента инерции в произвольных сечениях: 1)2ш:
, Законы изменения момента инерции в произвольных сечениях: 1)2ш: 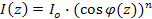
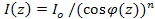 , n-число равное 0,1,2…,
, n-число равное 0,1,2…,  - момент инерции сечения в замке.
- момент инерции сечения в замке.
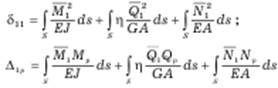 где S – длина оси арки; ds – бесконечно малый элемент оси; EJ, GA, EA – жесткости сечения соответственно при изгибе, сдвиге и растяжении-сжатии; η – коэффициент, учитывающий неравномерность распределения касательных напряжений по поперечному сечению при изгибе и зависящий от формы сечения.
где S – длина оси арки; ds – бесконечно малый элемент оси; EJ, GA, EA – жесткости сечения соответственно при изгибе, сдвиге и растяжении-сжатии; η – коэффициент, учитывающий неравномерность распределения касательных напряжений по поперечному сечению при изгибе и зависящий от формы сечения.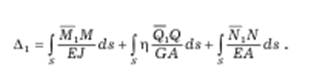 Равенство Δ 1 нулю говорит о правильности расчетов.
Равенство Δ 1 нулю говорит о правильности расчетов.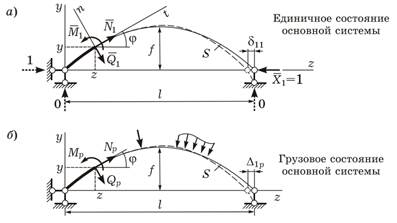
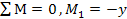 ,
,  ,
,  . Подставим полученные значения в формулу δ11 иΔ1р. При этом перейдем от интегрирования по длине оси s к интегрированию по длине пролета l.
. Подставим полученные значения в формулу δ11 иΔ1р. При этом перейдем от интегрирования по длине оси s к интегрированию по длине пролета l.  ƞdz
ƞdz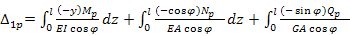 ƞdz.При приближенном расчете двухшарнирных арок со стрелой подъема f< l/3 и с высотой поперечного сечения h< l/10
ƞdz.При приближенном расчете двухшарнирных арок со стрелой подъема f< l/3 и с высотой поперечного сечения h< l/10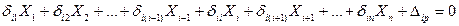

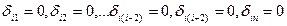 . Уравнение принимает вид:
. Уравнение принимает вид:  (8.21)
(8.21)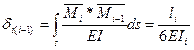



 (8.23)
(8.23)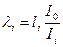 - приведенная длина i-го пролета.
- приведенная длина i-го пролета.

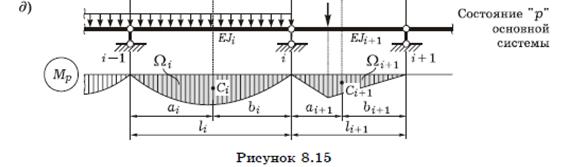
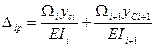
 - площадь эпюры Mp в i-м и (i + 1)-м пролетах; yCi - ордината эпюры Mi под центром тяжести Сi эпюры Mp в i-м пролете; yCi+1 - то же, в (i + 1)-м пролете; EJi, EJi + 1 - жесткости балки в i-м и (i + 1)-м пролетах.
- площадь эпюры Mp в i-м и (i + 1)-м пролетах; yCi - ордината эпюры Mi под центром тяжести Сi эпюры Mp в i-м пролете; yCi+1 - то же, в (i + 1)-м пролете; EJi, EJi + 1 - жесткости балки в i-м и (i + 1)-м пролетах.