
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о взаимности единичных реакций и перемещений в статически неопределимых системах (вторая теорема Рэлея).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте На рис. показаны два состояния произвольной статически неопределимой системы (рамы). В первом состоянии (состоянии i) на раму действует обобщённая сила Fi = 1. Опорная связь j получает единичное перемещение во втором состоянии (состоянии j). Введём обозначения: r'ji – реакция в j-й связи от обобщённой силы Fi = 1 в состоянии i,
Для состояний i и j используем теорему о взаимности возможных работ внешних сил А ij=1*δ’ij + r’ji*1 Возможная работа А ji внешних сил состояния j на перемещениях, вызываемых внешними силами состояния i, равна нулю, так как в состоянии i перемещения по направлению опорных связей в том числе и по направлению связи j, отсутствуют, т.е. А ji=0 В соответствии с выражением А ij= А ji, поэтому 1*δ’ij + r’ji*1=0 -δ’ij = r’ji Соотношение является математической формулировкой теоремы о взаимности реакций и перемещений: реакция в j-й связи от силы Fi = 1 с обратным знаком численно равна перемещению в направлении i-й силы от смещения j-й связи на единицу.
Предельным пластичным состоянием сечения называется такое состояние, при котором во всех точках сечения напряжение равно пределу текучести.
Мpl=ϬyWpl Wpl-пластический момент сопротивления для сим. сечения Wpl=2Sx* Sx*- статический момент полусечения Методика расчета статически-определимых балок Целью расчета является определение предельной нагрузки, при которой в опасном сечении возникает предельное состояние. Строится эпюра моментов в упругой стадии работы. По ней выбирается опасное сечение. Момент в опасном сечении приравнивается к предельному моменту, при этом нагрузка обозначается как предельная. Выражается предельная нагрузка через предельный момент.
Ful/4=Mpl= ϬyWpl Fu=Mpl*4/l=4 ϬyWpl/l
Расчет статически неопределимых балок с учетом пластических деформаций. Для статически неопределимых балок образование одного пластического шарнира не приводит к исчерпанию несущей способности, т.к. в этом случае степень кинематической определимости системы снижается на одну единицу. В случае n раз статически неопределимой балки исчерпание несущей способности происходит при формировании n + 1 пластических шарниров. Однако в ряде случаев часть балки может стать геометрически изменяемой при значительно меньшем числе пластических шарниров. Например, в статически многократно неопределимой балке с консолью (рис.20.12), несущая способность заданной системы исчерпается в случае возникновения первого же пластического шарнира над крайней правой опорой.
Рис. 20.12
Для расчета статически неопределимых систем по теории предельного равновесия можно воспользоваться одним из двух способов - кинематическим или статическим. При применении кинематического способа, в предельном состоянии составляется уравнение работы всех внешних и внутренних усилий на основе принципа возможных перемещений. Этот принцип формулируется так: если система твердых тел находится в равновесии под действием системы сил, то работа, совершаемая этими силами на любом малом возможном перемещении системы, должна быть равна нулю. При применении статического способа при отсутствии упругого расчета, на основе которого, предварительно можно определить наиболее вероятную схему разрушения конструкции, задаются различные схемы разрушения предельной стадии работы рассматриваемой системы, и для каждой из них составляются уравнения равновесия и определяются предельные значения внешних сил. Из их числа, наименьшая является расчетной величиной предельной силы. Из числа рассмотренных схем разрушения, на основании которых определяется предельная сила, является наиболее вероятной схемой, разрушения конструкции.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 755; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 – перемещение по направлению обобщённой силы Fi = 1 от смещения связи j на единицу в состоянии j. За положительное направление перемещения
– перемещение по направлению обобщённой силы Fi = 1 от смещения связи j на единицу в состоянии j. За положительное направление перемещения 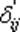 примем перемещение, происходящее по направлению обобщённой силы Fi = 1, а за положительную реакцию r'ji реакцию, направление которой совпадает с перемещением j-й связи.
примем перемещение, происходящее по направлению обобщённой силы Fi = 1, а за положительную реакцию r'ji реакцию, направление которой совпадает с перемещением j-й связи.






