
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статисеские неопределимая. Основная, эквивалентная система.Содержание книги
Поиск на нашем сайте
Статисеские неопределимая. Основная, эквивалентная система. Конструкции, в которых число неизвестных связей превышает число уравнений равновесия, получаемых для плоской или пространственной системы. Такие системы называются статически неопределимыми. Система, полученая из заданной неопределимой системы. Путем отбрасывания лишних связей, называется основной системой. Если к основной системе приложить все заданные нагрузки и неизвестные, то получим эквивалентную систему.
Пластический момент при кручении. Стержни круглого или кольцевого сечения, работающие на кручение, называют валами. При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п. Величина Wp называетсяпластическим моментом сопротивления при кручении. Внецентревое растяжение-сжатие. Внецентренное сжатие – это вид деформации, при котором продольная сила в поперечном сечении стержня приложена не в центре тяжести. При вне центренном сжатии, помимо продольной силы (N), возникают два изгибающих момента ( Считают, что стержень обладает большой жесткостью на изгиб, чтобы пренебречь прогибом стержня при внецентренном сжатии. Задача о внецентренном сжатиистержня впервые была рассмотрена Т. Юнгом. Малоцикловая усталость Под малоцикловой усталостью следует считать разрушение материалов, происходящее на протяжение сотен циклов. Малая долговечность сотен циклов наблюдается при условиях, когда в течение каждого цикла нагружается сначала в прямом, а затем в обратном направлении. Малоцикловая усталость в большинстве случаев связана с действием высоких напряжений, поэтому изломам присущи особенности строения, характерные для изломов циклической перегрузки или типично усталостных изломов в зонах, примыкающих к долому. Изломы малоцикловой усталости отличают многооча-говость и вследствие этого расположение зоны долома, близкое к центру сечения образца (при изгибе вращающегося образца), относительно малая длина усталостной трещины и т. д. 5. Третья и четвертая теория прочности. 3 – Теория наибольших косательных напряжений. По этой теории прочности: независимо от вида напряженного состояния предельное состояние наступит когда касательные напряжения достигнет предельного значение. Касательное напряжение в 1,75 раз опаснее нормального. 4-я
Предельное состояние наступит тогда, когда накапливается потенциальная энергия и достигает предельного состояния. По этой теории прочности не учитывается второе (главное) напряжение, такое допущение позволяет совершено спонтанно увеличить размеры деталей, иногда на 20% увеличивали экономические расходы на эту деталь. Удар при кручении. Удар - это происходящее в результате соприкосновения взаимодействие движущихся тел. Определение деформаций и напряжение при ударе с кручением мало отличается от ударного растяжения (сжатия) или ударного изгиба.
T- кинетическая энергия тела. Определен ие напряжений при устойчивости Под напряжение следует понимать силы взаимодействия между частицами элемента, приходящиеся на единицу площади Устойчивость – это способность конструкции сохранять положение равновесия, отвечающее действующей на нее нагрузке. Положение равновесия конструкции устойчиво в том случае, если, получив малое отклонение (возмущение) от этого положения равновесия, конструкция снова к нему возвращается. Проблема устойчивости возникает, в частности, при расчете сжатых колонн. Может случиться так, что при критической нагрузке колонна, отвечающая и условию прочности, и условию жесткости, внезапно изогнется (потеряет устойчивость). Это может привести к разрушению всей конструкции. Анизотропия прочности. Анизотропия прочности, которую следует отличать от анизотропии упругих свойств материала и сопротивления пластическому деформированию, понимается зависимость величины разрушающих напряжений от положения их главных осей относительно системы координат, неизменно связанной с рассматриваемым телом(древесина). Оси X, Y, Z называются главными осями анизотропии.
Это ортогональная анизотропия. Она встречается чаще других. Гипербола Эйлера
Нетрудно заметить что при малых гибкостях формула Эйлера даёт преувеличение значения критического напряжения, а так же и критической силы. Так как величина модуля Упругости Материала, входящая в формулы для вычисления δk и Рк,остается ПОСТОЯННОЙ лишь в пределах применимости закона Гука, то определить по Эйлера критическое напряжение превышающие предел пропорциональности δпр нельзя:
Абсциса точки К отвечает наименьшему значению гибкости стержня, при котором формула Эйлера ещё оказывается верной
12, Виды деформаций в природе: При описании механических свойств материалов принято различать два основных вида деформации: упругую и пластическую. Упругая деформация обратима, т.е. она исчезает либо одновременно со снятием напряжения, либо постепенно во время отдыха материала после разгрузки. Пластическая деформация необратима, т.е. она не исчезает после снятия напряжения. Если пластическая деформация связана с напряжением вне зависимости от временных характеристик процесса нагружения, то такую деформацию называют мгновенно упругой εму или соответственно мгновенно пластической εмп в случае, когда соотношения связывающие деформацию с напряжением включают в качестве дополнительного параметра физическое время, эту деформацию называют вязкоупругой εву или, соответственно вязкопластической εвп. Полная равна сумме всех четырёх
Формула Ясинского Если гибкость стержня меньше предельного значения
где a, b постоянные, зависящие от материала. Ядро сечения
Облость расположенная вокруг центра сечения, в пределах которой должна находиться точка приложения продольной сжимающейся или растягивающейся силы, что бы напряжения в сечении были одного знака, называется ядром сечения Границы ядра сечения определяются
Где Уа и Ха – координаты точек на контуре ядра сечения Ау и Ах – координаты точек, к которых нейтральная линия касается контура сечения. Уравнение Максвела.
Гибкость стержней Гибкость стержня — отношение расчетной длины стержня
Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба Расчетная длина
Соответственно коэффициент При расчетах элементов железобетонных конструкций к гибкости предъявляются требования по её ограничению. Также, в зависимости от гибкости назначается величина армирования. В расчетах стальных конструкций гибкость имеет наибольшее значение ввиду большой прочности стали с вытекающей из этого формой элементов(длинные, небольшой площади) из-за чего исчерпание несущей способности по устойчивости наступает до исчерпания запаса прочности по материалу.
34 Практические примеры определения повреждений Механизм усталостного разрушения имеет сложное развитие и зависит от многих факторов (материала, вида напряженного состояния, условий работы и т.д.). Эксперименты показывают, что характерной особенностью процесса разрушения при циклических напряжениях является возникновение в материале (иногда задолго до разрушения) мельчайших трещинок, являющихся следствием развития сдвигов в кристаллической решетке. Трещинки концентрируются, как правило, на поверхности материала или в поверхностных слоях в тех местах, где сделано недостаточное плавное изменение формы и размеров детали, где имеются поверхностные повреждения (заусеницы, царапины или внутренние дефекты материала, неметаллические включения, поры, раковины и т.п.). Мельчайшие трещинки постепенно развиваются, увеличиваются в размерах, сливаются в одну или несколько больших трещин и настолько ослабляют поперечное сечение детали, что она разрушается, будучи не в состоянии противостоять действию внешней нагрузки. Разрушение сопровождается доломом или дорывом детали, и в местах разрушения, как правило, наблюдается шейка, подобно той, как это имеет место при кратковременном деформировании образца. Поэтому разрушение детали при переменных напряжениях происходит обычно внезапно. В месте излома детали всегда можно видеть две зоны: гладкую и зернистую. При переменных напряжениях края трещины то сближаются и нажимают друг на друга, то расходятся. Этим и объясняется наличие гладкой, притертой зоны излома. Зернистая зона – результат внезапного разрушения. Таким образом, под влиянием усталости необходимо понимать явление постепенного развития трещины при переменных напряжениях, приводящее к постепенному внезапному разрушению, не сопровождающемуся сколько-нибудь пластическими деформациями. 35. Расчет винтовых пружин. Простой пример применения теоремы Кастильяно к определению перемещений — это расчет винтовой пружины. Приводя направленную по оси силу центру тяжести сечения получим пару с моментом. Разлагая момент этой пары на направление касательной к винтовой линии и перпендикулярное, найдем крутящий момент
Так как моменты всюду постоянны, то формулы выше дадут:
Перемещение точки приложения силы, то есть вытяжка пружины:
Расчет пружины на прочность в случае, если сечение круглое, производится так. Наибольшее напряжение изгиба
Наибольшее напряжение кручения
На практике обычно применяются пружины с малым углом подъема винта. Подбор сечения стержней При решении задач на подбор сечений в стержнях в большинстве случаев используется следующий план: 1) Через продольные силы в стержнях определяем расчётную нагрузку. 2) Далее через условие прочности осуществляем подбор сечений согласно ГОСТ. 3) Затем определяем абсолютные и относительные деформации. При малых усилиях в сжатых стержнях подбор сечения производится по заданной предельной гибкости λпр. Сначала определяется требуемый радиус инерции: Ползучесть материалов Ползучесть материалов - медленная непрерывная пластическая деформация твёрдого тела под воздействием постоянной нагрузки или механического напряжения. Ползучести в той или иной мере подвержены все твёрдые тел, как кристаллические, так и аморфные. Ползучесть наблюдают при растяжении, сжатии, кручении и других видах нагружения. Ползучесть описывается так называемой кривой ползучести, которая представляет собой зависимость деформации от времени при постоянных температуре и приложенной нагрузке. Полная деформация в каждую единицу времени представляет собой сумму деформаций ε = εе + εр + εс, где εе — упругая составляющая; εр - пластическая составляющая, возникающая при возрастании нагрузки от 0 до Р; εс — деформация ползучести, возникающая с течением времени при σ = const.
Ударная вязкость Ударная вязкость — способность материала поглощать механическую энергию в процессе деформации и разрушения под действием ударной нагрузки. Основным отличием ударных нагрузок от испытаний на растяжение-сжатие или изгиб является гораздо более высокая скорость выделения энергии. Таким образом, ударная вязкость характеризует способность материала к быстрому поглощению энергии. Обычно оценивается работа до разрушения или разрыва испытываемого образца при ударной нагрузке, отнесённой к площади его сечения в месте приложения нагрузки. Выражается в Дж/см2 или в кДж/м2. Определяется отношением работы W, затраченной на разрушение образца, к площади поперечного сечения А в месте излома: аК=W/A. Расчёт кислородных баллонов Баллоны являются разновидностью сосудов, но к ним предъявляются дополнительные требования. Расчет баллонов проводится при условии, чтобы напряжения в их стенках при гидравлическом испытании не превышали 90% предела текучести для данной марки стали. Толщина стенки (м) цилиндрической части баллона: Где P-рабочее давление, Па; DB –внутренний диаметр баллона, см; RP- допускаемое напряжение на разрыв, Па; При расчете прочности баллонов на действие внутреннего давления коэффициент запаса прочности (к пределу текучести) принимается не менее 3 - для баллонов, изготовленных из бесшовных труб, и не менее 3,5 - для сварных баллонов.Баллоны новых конструкций или изготовленные из неприменявшихся ранее материалов (несколько штук из головной партии) подвергаются разрушению под действием гидравлического давления. При этом запас прочности должен быть не менее 2,6 с пересчетом на нижний предел прочности металла и наименьшую толщину стенки без прибавки на коррозию.
Ядро сечения Ядро сечения - это малая область вокруг центра тяжести поперечного сечения. Ядро сечения характеризуется тем, что всякая сжимающая продольная сила, приложенная внутри него, вызывает во всех точках поперечного сечения напряжения сжатия. Понятие ядро сечения ввел Бресс в 1854 г. Для прямоугольника ядро сечения имеет форму ромба (рис. 10.3, а), а для круглого сплошного стержня ядро сечения – круг (рис. 10.3, б).
Статисеские неопределимая. Основная, эквивалентная система. Конструкции, в которых число неизвестных связей превышает число уравнений равновесия, получаемых для плоской или пространственной системы. Такие системы называются статически неопределимыми. Система, полученая из заданной неопределимой системы. Путем отбрасывания лишних связей, называется основной системой. Если к основной системе приложить все заданные нагрузки и неизвестные, то получим эквивалентную систему.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.253.199 (0.008 с.) |

 и
и  ).
). центральное растяжение или сжатие.
центральное растяжение или сжатие.
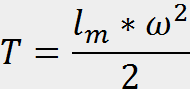
 - угловая скорость вращения маховика,
- угловая скорость вращения маховика,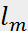 -массовый момент инерции маховика
-массовый момент инерции маховика
 Зависимость графически изображается кривой, обычно называемой гиперболой Эйлера. Асимптотами служат оси координат δk и λ
Зависимость графически изображается кривой, обычно называемой гиперболой Эйлера. Асимптотами служат оси координат δk и λ
 , откуда
, откуда 
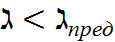 то формула Эйлера становится неприменимой, так как критические напряжения превышают предел пропорциональности и закон Гука неприменим. В этих спучаях критическое напряжение определяют по эмпирическим формулам, полученным на основании опытов и приведенных в справочниках. Одна из этих формул - формула Ясинского
то формула Эйлера становится неприменимой, так как критические напряжения превышают предел пропорциональности и закон Гука неприменим. В этих спучаях критическое напряжение определяют по эмпирическим формулам, полученным на основании опытов и приведенных в справочниках. Одна из этих формул - формула Ясинского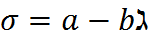

 =
=  ;
; 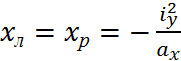

 к наименьшему радиусу инерции
к наименьшему радиусу инерции  его поперечного сечения.
его поперечного сечения.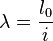
 . Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом.
. Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом. , где
, где — коэффициент, зависящий от условий закрепления стержня, а
— коэффициент, зависящий от условий закрепления стержня, а  — геометрическая длина. Расчетная длина, также называется привиденной или свободной.
— геометрическая длина. Расчетная длина, также называется привиденной или свободной. , при обоих защемленных концах
, при обоих защемленных концах  . Формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка
. Формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка  и выше.
и выше. и изгибающий момент
и изгибающий момент 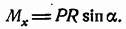





 а по радиусу инерции подбираются соответствующие уголки. Для облегчения определения необходимых габаритов сечения, позволяющих наметить необходимые размеры уголков, в таблице “Приблеженные значения радиусов” инерций сечений элементов из уголков приведены приближенные значения радиусов инерции для различных сечений элементов из уголков.
а по радиусу инерции подбираются соответствующие уголки. Для облегчения определения необходимых габаритов сечения, позволяющих наметить необходимые размеры уголков, в таблице “Приблеженные значения радиусов” инерций сечений элементов из уголков приведены приближенные значения радиусов инерции для различных сечений элементов из уголков.  ,
,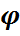 - коэффициент прочности (применяют для бесшовных баллонов =1, а для сварных =0,7); С- прибавка на минусовые допуски, см.
- коэффициент прочности (применяют для бесшовных баллонов =1, а для сварных =0,7); С- прибавка на минусовые допуски, см.



