
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как влияют упругие свойства материала системы при удареСодержание книги
Поиск на нашем сайте
При ударе выполняется закон сохранения импульса и закон сохранения момента импульса, но обычно не выполняется закон сохранения механической энергии. Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Математическая модель абсолютно упругого удара работает примерно следующим образом: 1. Есть в наличии два абсолютно твердых тела, которые сталкиваются 2. В точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно переходит в энергию деформации. 3. В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации вновь переходит в кинетическую энергию. 4. Контакт тел прекращается и они продолжают движение. Для математического описания простейших абсолютно упругих ударов, используется закон сохранения энергии и закон сохранения импульса.
Здесь m1, m2 - массы первого и второго тел. u1, v1 - скорость первого тела до, и после взаимодействия. u2, v2 - скорость второго тела до, и после взаимодействия.
Важно - импульсы складываются векторно, а энергии скалярно. Определение критической силы Впервые проблема устойчивости сжатых стержней была поставлена Леонардом Эйлером. Эйлер вывел расчетную формулу для критической силы и показал, что ее величина существенно зависит от способа закрепления стержня. Идея метода Эйлера заключается в установлении условий, при которых кроме прямолинейной возможна и смежная форма равновесия стержня при постоянной нагрузке. Для шарнирно закрепленного, центрально-сжатого стержня постоянного сечения Формула Эйлера имеет вид:
Кинетические уравнение повреждений второго типа Кинетическое уравнение, в котором величина меры повреждений зависит не только от истории нагружения, а также и от мгновенных значений нагружений. Такие уравнения имеют вид:
Простейшим примером может служить соотношение
Интегрируя (15.12) по При
где Рассмотрим подробнее уравнение (15.14). Наглядная трактовка этого уравнения представлена на рисунке (15.4). К моменту
Рисунок 15.4 – Трактовка зависимости (15.14)
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.90 (0.007 с.) |





 - приведенная длина стержня;
- приведенная длина стержня;  - коэффициент приведения длины.Выражение "приведенная длина" означает, что в формуле Эйлера с помощью коэффициента
- коэффициент приведения длины.Выражение "приведенная длина" означает, что в формуле Эйлера с помощью коэффициента  .Формула Эйлера применима только о пределах выполнения закона Гука, когда критическое напряжение
.Формула Эйлера применима только о пределах выполнения закона Гука, когда критическое напряжение  не превышает предел пропорциональности материала стержня, так как эта формула была введена с помощью зависимости
не превышает предел пропорциональности материала стержня, так как эта формула была введена с помощью зависимости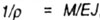 в свое время полученной на основании закона Гука. Применимость формулы Эйлера можно определить, оценив гибкость стержня и сравнив эту гибкость с ее предельным значением.
в свое время полученной на основании закона Гука. Применимость формулы Эйлера можно определить, оценив гибкость стержня и сравнив эту гибкость с ее предельным значением. . (15.11)
. (15.11) . (15.12)
. (15.12) , получаем:
, получаем:  . (15.13)
. (15.13) имеем
имеем  , откуда по условию разрушения
, откуда по условию разрушения  , получается, что
, получается, что  , где
, где  – сопротивление мгновенному разрушению. Из выражения (15.13) получается следующее условие разрушения при любом режиме нагружения:
– сопротивление мгновенному разрушению. Из выражения (15.13) получается следующее условие разрушения при любом режиме нагружения: , (15.14)
, (15.14) – напряжение, приводящее к разрушению в момент
– напряжение, приводящее к разрушению в момент  сопротивление мгновенному разрушению снизилось от величины
сопротивление мгновенному разрушению снизилось от величины  до величины
до величины  . Для разрушения материала требуется догрузка на величину
. Для разрушения материала требуется догрузка на величину  . В некоторый момент времени эта разница может быть равной нулю, и разрушение при этом режиме эксплуатации произойдет без догрузки.
. В некоторый момент времени эта разница может быть равной нулю, и разрушение при этом режиме эксплуатации произойдет без догрузки.



