Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт статически неопределимых опорных балокСодержание книги
Поиск на нашем сайте Система называется статически определимой, если внутренние усилия в ее элементах и реакции связей можно определить из условий равновесия статики.Для Расчёта статически неопределимых балок можно использовать метод сил: устанавливается степень статической неопределимости системы, отбрасываются дополнительные связи, их действие заменяется неизвестными реакциями и записываются условия равенства нулю перемещений по направлению отброшенных связей.Эти уравнения называются уравнениями совместности деформаций или каноническими уравнениями метода сил. Коэффициенты канонических уравнений, представляющие собой линейные или угловые перемещения, обычно определяются энергетическими методами.Совместное решение уравнений статики и уравнений совместности деформаций дает возможность определить реакции всех связей.
32.ПРЕДЕЛ ВЫНОСЛИВОСТИ За базовое, т.е. наибольшее число циклов из задаваемых при испытаниях принимают для черных металлов 107 циклов нагружения, а для цветных – 108. Индекс в обозначении предела выносливости соответствует коэффициенту асимметрии цикла напряжений при испытаниях. Так, для симметричного цикла предел выносливости обозначается σ–1, а для отнулевого – σ0. Гибкость стержней Гибкость стержня — отношение расчетной длины стержня
Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба Расчетная длина
Соответственно коэффициент При расчетах элементов железобетонных конструкций к гибкости предъявляются требования по её ограничению. Также, в зависимости от гибкости назначается величина армирования. В расчетах стальных конструкций гибкость имеет наибольшее значение ввиду большой прочности стали с вытекающей из этого формой элементов(длинные, небольшой площади) из-за чего исчерпание несущей способности по устойчивости наступает до исчерпания запаса прочности по материалу.
34 Практические примеры определения повреждений Механизм усталостного разрушения имеет сложное развитие и зависит от многих факторов (материала, вида напряженного состояния, условий работы и т.д.). Эксперименты показывают, что характерной особенностью процесса разрушения при циклических напряжениях является возникновение в материале (иногда задолго до разрушения) мельчайших трещинок, являющихся следствием развития сдвигов в кристаллической решетке. Трещинки концентрируются, как правило, на поверхности материала или в поверхностных слоях в тех местах, где сделано недостаточное плавное изменение формы и размеров детали, где имеются поверхностные повреждения (заусеницы, царапины или внутренние дефекты материала, неметаллические включения, поры, раковины и т.п.). Мельчайшие трещинки постепенно развиваются, увеличиваются в размерах, сливаются в одну или несколько больших трещин и настолько ослабляют поперечное сечение детали, что она разрушается, будучи не в состоянии противостоять действию внешней нагрузки. Разрушение сопровождается доломом или дорывом детали, и в местах разрушения, как правило, наблюдается шейка, подобно той, как это имеет место при кратковременном деформировании образца. Поэтому разрушение детали при переменных напряжениях происходит обычно внезапно. В месте излома детали всегда можно видеть две зоны: гладкую и зернистую. При переменных напряжениях края трещины то сближаются и нажимают друг на друга, то расходятся. Этим и объясняется наличие гладкой, притертой зоны излома. Зернистая зона – результат внезапного разрушения. Таким образом, под влиянием усталости необходимо понимать явление постепенного развития трещины при переменных напряжениях, приводящее к постепенному внезапному разрушению, не сопровождающемуся сколько-нибудь пластическими деформациями. 35. Расчет винтовых пружин. Простой пример применения теоремы Кастильяно к определению перемещений — это расчет винтовой пружины. Приводя направленную по оси силу центру тяжести сечения получим пару с моментом. Разлагая момент этой пары на направление касательной к винтовой линии и перпендикулярное, найдем крутящий момент
Так как моменты всюду постоянны, то формулы выше дадут:
Перемещение точки приложения силы, то есть вытяжка пружины:
Расчет пружины на прочность в случае, если сечение круглое, производится так. Наибольшее напряжение изгиба
Наибольшее напряжение кручения
На практике обычно применяются пружины с малым углом подъема винта.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 к наименьшему радиусу инерции
к наименьшему радиусу инерции  его поперечного сечения.
его поперечного сечения.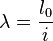
 . Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом.
. Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом. , где
, где — коэффициент, зависящий от условий закрепления стержня, а
— коэффициент, зависящий от условий закрепления стержня, а  — геометрическая длина. Расчетная длина, также называется привиденной или свободной.
— геометрическая длина. Расчетная длина, также называется привиденной или свободной. , при обоих защемленных концах
, при обоих защемленных концах  . Формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка
. Формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка  и выше.
и выше. и изгибающий момент
и изгибающий момент