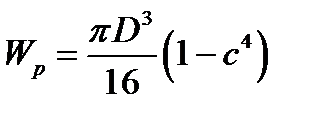Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о напряжениях, деформациях и перемещениях.Содержание книги
Поиск на нашем сайте
Рабочие гипотезы СОПРОМАТА ОТВЕТ: В отличие от термеха, базирующегося на модели абс. твердого тела, в сопромате принята своя расчетная модель-модель идеализированного деформируемого тела. А для упрощения расчетов принимаются следующие допущения или гипотезы: 1) Материал тела имеет сплошное строение. 2) материал однороден, т.е. во всех точках свойства одинаковы. 3) материал изотропен, т.е. по всем направлениям свойства одинаковы. 4) до приложения внешних сил начальные напряжения в материале отсутствуют. 5) при решении реальных задач целесообразно использовать принцип суперпозиции, или принцип независимости действия сил, т.е. воздействие на конструкцию группы сил равно сумме воздействий от каждой силы в отдельности и не зависит от последовательности приложения этих сил. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И МЕТОД ИХ ОПРЕДЕЛЕНИЯ. ОТВЕТ: Под действием внешних сил на брус возникают внутренние силы или внутренние силовые факторы, для определения которых в сопромате принят единый расчетный метод – метод сечений. 1) разрезаем мысленно брус в исследуемом сечении на 2 части I и II. 2) Отбрасываем одну из частей. 3) Заменяем действие отбрасываемой части II на часть I внутренними силовыми факторами(в общем случае их 6). Qx Qy – поперечные силы, Nz – продольная сила, Mx My – изгибающие моменты, Mz – крутящий момент. 4) Уравновешиваем оставшуюся часть бруса и с помощью уравнений равновесия термеха находим искомые силовые факторы.
ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ. ОТВЕТ: Мерой интенсивности действия внутренних сил в окрестности точки рассматриваемого поперечного сечения являются напряжения, определяемые отношением силы к единице площади [Па]. Если в поп. сечении выделить элемент DА, к которому будет приложена сила DР, то DР/DА=рm – среднее полное напряжение в рассматриваемой точке поперечного сечения. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТУПЕНЧАТЫХ БРУСЬЯХ С НЕСКОЛЬКИМИ СИЛОВЫМИ УЧАСТКАМИ. ОТВЕТ: Растяжением или сжатием бруса называют такой его вид деформации, при котором все внешние силы направлены по продольной оси, а в поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N. Ее величину определяют, используя метод сечений: Напряжения и деформации при осевом растяжении-сжатии В процессе деформирования в поперечных сечениях бруса при осевом растяжении-сжатии возникают только нормальные напряжения σ, причем они распределяются равномерно по поперечному сечению. При растяжении-сжатии брус испытывает только линейные деформации.
Связь между Линейная закономерность, связывающая напряжения и деформации – закон Гука при осевом растяжении-сжатии.
Определение геом. характеристик. Рассмотрим определение геом. характеристик 1.Сплошной вал
3.Тонкостенное трубчатое сечение
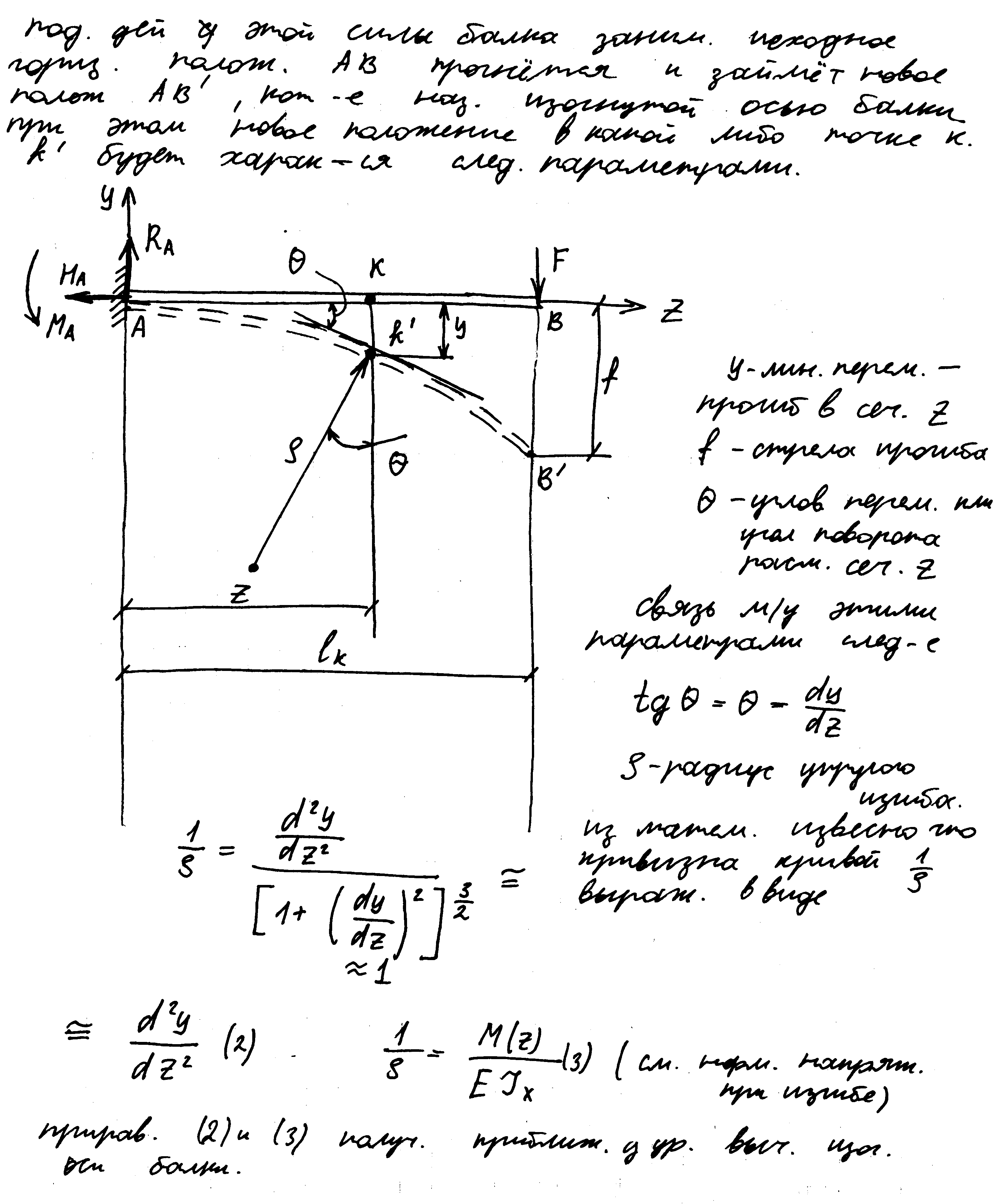
К тонкостенным отн-ся трубу с соотношением Определение перемещений при изгибе. Условие жесткости. Дифференциальное уравнение изогнутой оси балки.
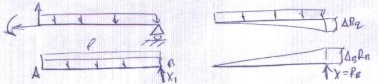
Варианты расчета простых статически неопределимых балок Существует несколько способов расчета простых балок: 1.Сравнение линейных перемещений.
ΔВ=ΔВq+ΔBRB=0(1) доп. уравнение деформаций
Слагаемые в(1) могут быть найдены исп-я готовые таблицы или универсальные уравнения. Применительно к рас-му предмету: ΔBq=-qe4/8EIx; ΔBRB=RBe3 /3EIx;
ΔB=-qe4/8EIx +RBe3/3EIx =0 =>RB=3qe/8
2. Сравнение угловых перемещений. Можно отбросить связь, препятствующая повороту опорного сечения А и записать
ΔA=ΔAq+ΔAMA=0(2) Также ур-е деформации слагаемое означает углы поворота.
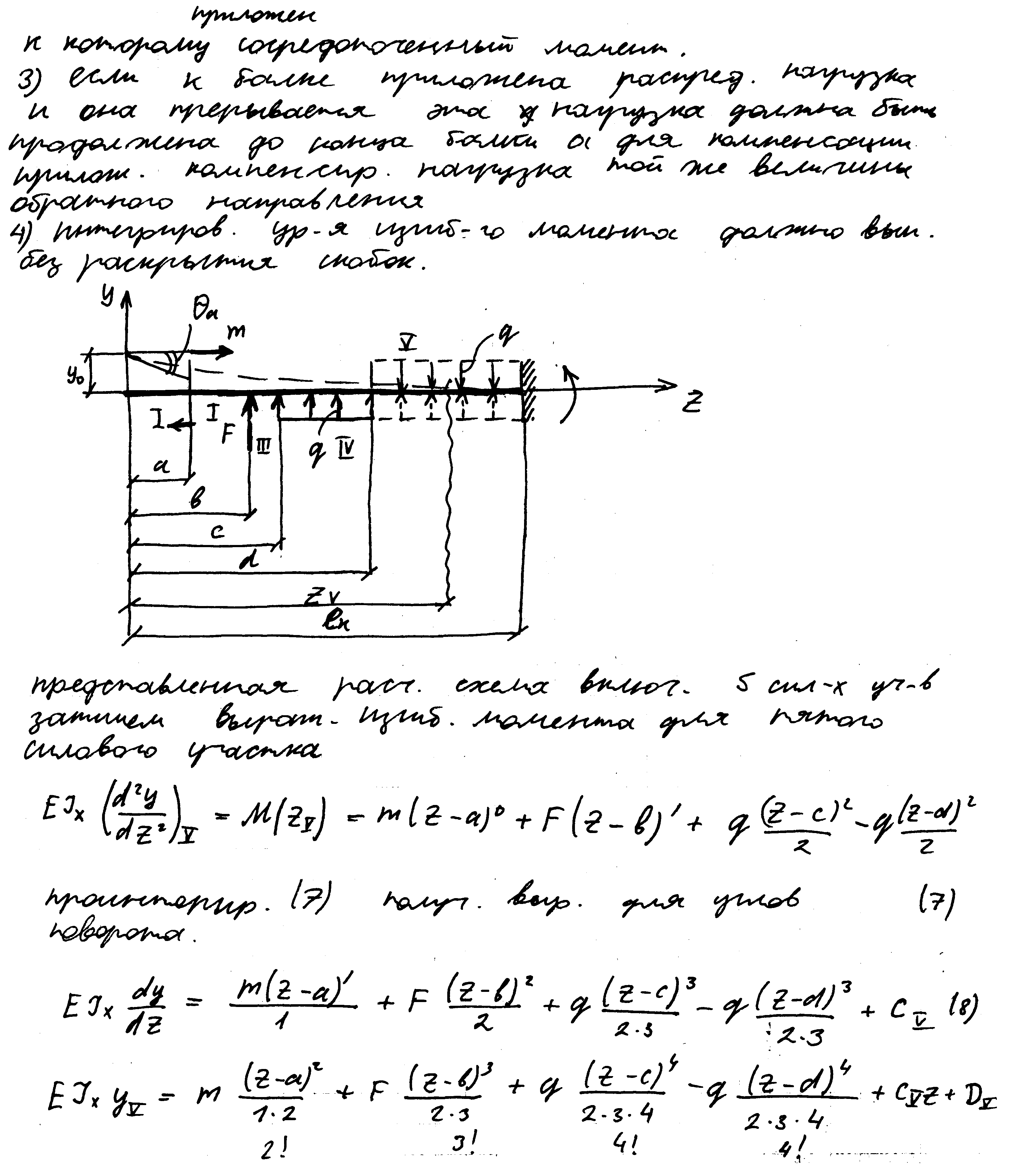
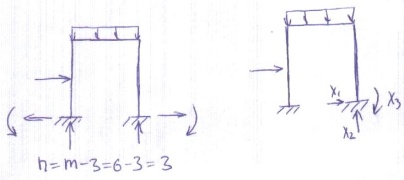
3.Составление замкнутой системы ур-я. 3 ур-я статики+ унивес. ур-е yB=0. 43. Метод сил для расчета сложных СНС. Метод при котором за неизвестное принимаются сосредоточенные моменты наз-ся методом сил. Он явл-ся наиболее распространенным и ис-ся для любых упругих систем (балки, рамы,эстакады итд.). Например: К трем ур-ям статики для решения данной СНС добавится 3 уравнения, выражающие рав-во 0 перемещений по направлениям всех отброшенных связей т.е. опорное сечение и не перемещаются им в горизонтальном или в вертикальном перемещениях и не переворачиваются. X1 Δ1=0 X2 Δ2=0 (1) X3 Δ3=0 Каждое уравнение системы(1) можно записать в развернутом виде: Δ1=Δ11+Δ12+Δ13+Δ1f=0 (2) Первый символ указывает направление; 2-й воз-е. Δ1f-перемещение опорного сечения А в направлении действия X, вызванное внешней нагрузкой (2) можно выразить через единичные перемещения и искомое неизвестное (это первые три слагаемых) Δ11=δ11-x1 и тогда система примет закончен. вид. δ11 x1+ δ12 x2+ δ13 x3+ Δ1f=0 δ21 x1+ δ22 x2+ δ23 x3+ Δ2f=0 (3)-система кумс. δ31 x1+ δ32 x2+ δ33 x3+ Δ3f=0 Канонические ур-я метода сил-КУМС. Число ур-й равно степени статической неопределимости.
Рабочие гипотезы СОПРОМАТА ОТВЕТ: В отличие от термеха, базирующегося на модели абс. твердого тела, в сопромате принята своя расчетная модель-модель идеализированного деформируемого тела. А для упрощения расчетов принимаются следующие допущения или гипотезы: 1) Материал тела имеет сплошное строение. 2) материал однороден, т.е. во всех точках свойства одинаковы. 3) материал изотропен, т.е. по всем направлениям свойства одинаковы. 4) до приложения внешних сил начальные напряжения в материале отсутствуют. 5) при решении реальных задач целесообразно использовать принцип суперпозиции, или принцип независимости действия сил, т.е. воздействие на конструкцию группы сил равно сумме воздействий от каждой силы в отдельности и не зависит от последовательности приложения этих сил. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И МЕТОД ИХ ОПРЕДЕЛЕНИЯ. ОТВЕТ: Под действием внешних сил на брус возникают внутренние силы или внутренние силовые факторы, для определения которых в сопромате принят единый расчетный метод – метод сечений. 1) разрезаем мысленно брус в исследуемом сечении на 2 части I и II. 2) Отбрасываем одну из частей. 3) Заменяем действие отбрасываемой части II на часть I внутренними силовыми факторами(в общем случае их 6). Qx Qy – поперечные силы, Nz – продольная сила, Mx My – изгибающие моменты, Mz – крутящий момент. 4) Уравновешиваем оставшуюся часть бруса и с помощью уравнений равновесия термеха находим искомые силовые факторы.
ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ. ОТВЕТ: Мерой интенсивности действия внутренних сил в окрестности точки рассматриваемого поперечного сечения являются напряжения, определяемые отношением силы к единице площади [Па]. Если в поп. сечении выделить элемент DА, к которому будет приложена сила DР, то DР/DА=рm – среднее полное напряжение в рассматриваемой точке поперечного сечения.
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 1763; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.83.202 (0.01 с.) |

 - полное истинное напряжение. Вектор
- полное истинное напряжение. Вектор  раскладывают на
раскладывают на  и
и  .
.  - нормальное напряжение – вызывает разрушения путем отрыва.
- нормальное напряжение – вызывает разрушения путем отрыва.  - касательное напряжение – вызывает разрушение путем сдвига. Перемещения и деформации – понятия, характеризующие изменение размеров и формы исследуемого тела. При этом перемещения являются следствием деформации.
- касательное напряжение – вызывает разрушение путем сдвига. Перемещения и деформации – понятия, характеризующие изменение размеров и формы исследуемого тела. При этом перемещения являются следствием деформации. , т.е. продольная сила в рассматриваемом сечении бруса численно равна алгебраической сумме всех внешних сил, расположенных по одну сторону от сечения. Условились считать N>0, если она направлена в сторону от сечения, т.е. растягивает и N<0, если сжимает. Для полного суждения о прочности бруса необходимо построить график изменения продольной силы по длине бруса – эпюру продольной силы (Эп.N).
, т.е. продольная сила в рассматриваемом сечении бруса численно равна алгебраической сумме всех внешних сил, расположенных по одну сторону от сечения. Условились считать N>0, если она направлена в сторону от сечения, т.е. растягивает и N<0, если сжимает. Для полного суждения о прочности бруса необходимо построить график изменения продольной силы по длине бруса – эпюру продольной силы (Эп.N).
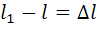 – абсолютная продольная деформация груза (удлинение)
– абсолютная продольная деформация груза (удлинение) - относительная продольная деформация
- относительная продольная деформация - абсолютная поперечная деформация (сужение)
- абсолютная поперечная деформация (сужение) - относительная поперечная деформация
- относительная поперечная деформация и
и 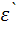 :
:  - коэффициент Пуассона.
- коэффициент Пуассона.


 ,
, 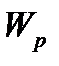 для наиболее часто встречаемых поперечных сечений валов.
для наиболее часто встречаемых поперечных сечений валов.


 2.Полый вал
2.Полый вал