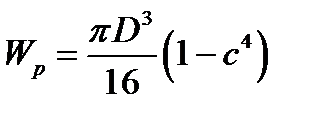Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет №14 классические теории (гипотезы) прочночсти.Содержание книги
Поиск на нашем сайте
Важнейшей практической задачей в инженерных расчетах является оценка прочности конструкции по известным напряженному состоянию. Эта задача решается с использованием одной из 4-х задач классических теорий (гипотез) прочности по следующей схеме.
Где [n]нормальный коэффициент запаса прочности. 1)Теория наибольших нормальных напряжений: Галилей; начало 18 века.: σэкв.=σ1: линейное напряженное состояние 2)Наибольших линейных деформаций; Эдлен Мариотас.1682 г.; σэкв 3)Наибольшие касательные напряжения; Шарль Кулон, 1773 г.: σэкв = σ1 - σ3 пластичные материалы в плоско напряженном состоянии. 4)Энергетическая М. Рубер. 1904 г.: σэкв= Данные опыта о скручивании круглого вала. Если на поверхность прямолинейного круглого вала нанести квадратную сетку линий //-х и I-ых продольной оси вала Z и приложить к концам внешние скруч. моменты, то после деформации вала можно убедиться в следующем: -ось вала осталась прямолинейной; -сечения вала плоские и I-ые к оси остались неизменными и после деформации, при этом расст-ие м/у смежными сечениями осталось неизменным; -торцевые сечения повернулись отн-но друг друга на некоторый угол
Напряжения и деформации при кручении вала круглого поперечного сечения. Определение деформаций. При кручении как было отмечено выше лин. деформаций не происходит,и под действием касат. напряжений
По аналогии с растяжением сжатием: ( Связь м/у модулями II рода: Определение напряжений (см.пред.стр.рис) Если на торцах вала выделить Выр-е (3) не позволяет опред-ить величину касат. напряжений
С учётом (4) выр-е (1) примет вид: Подставим (5) в (3): Угол закручивания,приходящийся на единицу длины вала наз-ся относит. углом закручивания вала и оппед-ся крутящим моментом Т и жесткостью поперечного сечения вала при кручении. Тогда подставив (6) в (5) получим з-н изменения касат. напряжений попереч. сечения вала.
Построение эпюры крутящего момента(Эп. Т) Величины крут. моментов будем опред. в попереч. сечениях вала, используя общепринятый в СМ метод сечений. Т= Определение геом. характеристик. Рассмотрим определение геом. характеристик 1.Сплошной вал
3.Тонкостенное трубчатое сечение
К тонкостенным отн-ся трубу с соотношением
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.39.176 (0.009 с.) |


 σ1 –
σ1 –  (σ2 – σ3) хрупкие материалы.
(σ2 – σ3) хрупкие материалы. пластичные материалы находящие в объемном состоянии.
пластичные материалы находящие в объемном состоянии. ,называемый углом закручивания, при этом прямолинейные радиусы на торцах не искривились; образующая на поверхности вала повернулась на искомую
,называемый углом закручивания, при этом прямолинейные радиусы на торцах не искривились; образующая на поверхности вала повернулась на искомую  ,называемый углом сдвига, и произошел перенос сетки(квадраты превратились в ромбы).
,называемый углом сдвига, и произошел перенос сетки(квадраты превратились в ромбы). Вывод: учитывая, что при кручении линейн. деформации отсутствуют, а есть только перенос сетки, в попереч. сечениях вала возникают только касат. напряжение
Вывод: учитывая, что при кручении линейн. деформации отсутствуют, а есть только перенос сетки, в попереч. сечениях вала возникают только касат. напряжение  , поскольку радиусы остались прямолинейными,
, поскольку радиусы остались прямолинейными, 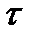 происходит перенос сетки(квадраты становятся ромбами, при этом max величины переноса
происходит перенос сетки(квадраты становятся ромбами, при этом max величины переноса  - абсолютный
- абсолютный  сдвиг, а отношение
сдвиг, а отношение  - относит.
- относит.  сдвиг.
сдвиг.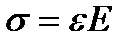 ) З-Н Гука применительно к кручению:
) З-Н Гука применительно к кручению: 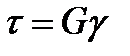 (1) G – модуль упругости II рода
(1) G – модуль упругости II рода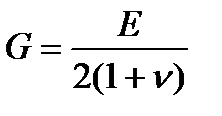 , для стали
, для стали 

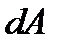 на раст-е
на раст-е  от оси,то на неё будет действовать сила
от оси,то на неё будет действовать сила 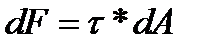 , а момент создаваемый этой силой будет
, а момент создаваемый этой силой будет 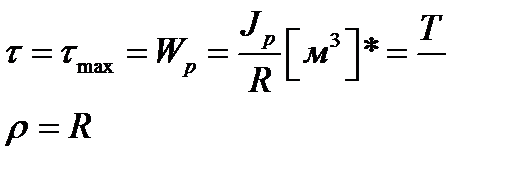 ,просуммировав по всей площади вала А,получим:
,просуммировав по всей площади вала А,получим:  (3)
(3) по известному крут. моменту Т (берём с эп.Т),поскольку не известен з-н изменения
по известному крут. моменту Т (берём с эп.Т),поскольку не известен з-н изменения 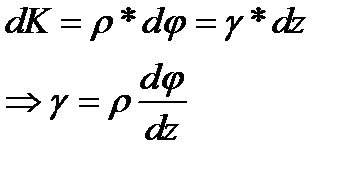 (4)
(4) (5)
(5) (6)
(6) (7)
(7) (в центре);
(в центре); (на поверх-ти вала) --
(на поверх-ти вала) --  (8)
(8) -полярный момент сопротивления поперечного сечения вала.
-полярный момент сопротивления поперечного сечения вала.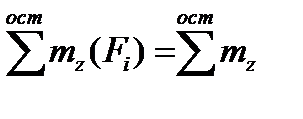 ,т.е. крут.момент в рассм-ом сечении вала численно равен алгебр. сумме внешних скручивающих моментов, расположенных по одну сторону от рассм. сечений. Условимся о след. правиле знаков: искомый крут. Момент Т будем считать «+»-ым, если наблюдатель на сечении смотрит со стороны нормали и видит его направленным против часовой стрелки(внешний скруч. момент m по часовой стрелки)
,т.е. крут.момент в рассм-ом сечении вала численно равен алгебр. сумме внешних скручивающих моментов, расположенных по одну сторону от рассм. сечений. Условимся о след. правиле знаков: искомый крут. Момент Т будем считать «+»-ым, если наблюдатель на сечении смотрит со стороны нормали и видит его направленным против часовой стрелки(внешний скруч. момент m по часовой стрелки) ,
, 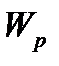 для наиболее часто встречаемых поперечных сечений валов.
для наиболее часто встречаемых поперечных сечений валов.


 2.Полый вал
2.Полый вал