
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение статически неопределимых задачСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Если число неизвестных реакций связи оказывается больше числа уравнений равновесия, то такая система является статически неопределимой. Разница между числом неизвестных реакций и числом уравнений равновесия определяет степень статической неопределенности системы. При решении статически неопределимых задач составляются недостающие уравнения, которые учитывают совместные перемещения в данной системе. С учетом известных перемещений предлагаются физические зависимости, например, в виде закона Гука, или в виде линейных температурных деформаций, для раскрытия сущности указанных совместных перемещений и, в дальнейшем, эти полученные уравнения решаются совместно. Этапы раскрытия статической неопределенности (рассмотрим на примере решения задачи данные по размерам и нагрузкам смотри на предыдущей странице): Статика – составление уравнений равновесия;
Геометрия – составление уравнений совместных перемещений;
Физика – определение физических соотношений между перемещениями и внутренними силами;
Синтез – совместное решение полученных уравнений. В уравнение п.2 подставим выражения для ∆li по закону Гука.
Определение внутренних напряжений:
Несмотря на то, что на участке СВ значение напряжений уменьшилось и составило 160МПа, условие прочности все равно не выполняется. Определение совместных перемещений:
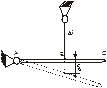
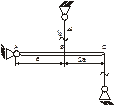
Обобщение: 1В статически неопределимых системах происходит перераспределение внутренних сил, напряжений и перемещений, по сравнению с аналогичными статически определимыми системами. 2Реакции связи а, следовательно, и внутренние силы, в статически неопределимых системах зависят от продольных и поперечных размеров, свойств материала и действия внешних сил. В статически определенных системах внутренние силы зависят только от внешних сил. 3Меняя жесткость системы подстановкой дополнительных связей, можно добиться рационального распределения внутренних сил при той же величине внешних нагрузок, в связи с этим так же меняются значения напряжений и перемещений. Б9: Температурные напряжения. Температурные напряжения Напряжение в стержне не изменится т.к. при нагревании он изменит свой размер (удлинится). В стержнях возникает напряжение сжатия. В статически определимой системе при изменении температуры напряжение не поменяется от действия температуры. Имеет место лишь перенос конструкции (см. рис.1). В статически неопределимой системе (см. рис. 2)
Решение задачи, расчетная схема которой приведена на рис. 2. Статика
Из подобия треугольников АВВ1 и АСС1 получаем
В первом стержне возникает сжимающее напряжение, т.к. балка под действием температуры поворачивается вниз и сжимает этот стержень. Во втором стержне тоже возникает напряжение сжатия, т.к. полная температурная деформация не может быть реализована из-за сопротивления первого стержня. Кроме того могут возникать монтажные напряжения. Совместные действия температурных и внешних нагрузок. Температурные напряжения при действии внешних нагрузок учитываются со своим знаком и могут как повысить так и понизить его. 1.Статика 3. Физика
С учетом совместных действий температурных напряжений и напряжений от действия силы Р получаем:
В первом стержне напряжение в целом повышается. Б10: Чистый сдвиг и его особенности. Расчеты на прочность при сдвиговых деформациях. Сдвиговая деформация Основы Под сдвиговой деформацией понимается такой вид деформации, когда в поперечном сечении балки действует только перерезывающая сила. При «чистом» сдвиге на гранях выделенного из бруса элемента действуют только касательные напряжения, и такие грани называются гранями «чистого» сдвига. (Рис.1)
При равномерном распределении касательных напряжений выражение (1) упрощается:
При расчете на сдвиг (срез) условия прочности с учетом зависимости (2) записываются в следующем виде:
Рассмотрим рис.2 Грань CD под действием касательных напряжений смещается относительно грани АВ и при этом мы получаем
Угол В пределах упругости выполняется закон Гука для сдвиговых деформаций (напряжение пропорционально относительным деформациям).
Здесь G – модуль сдвига, как и при растяжении, он характеризует упругие свойства материала при сдвиговых деформациях (модуль второго рода). С учетом коэффициента Пуассона можно представить соотношение между модулем второго и первого рода.
Заключение: Расчет из условий прочности на сдвиг используется при действии поперечных сил для различных соединений (заклепочные, сварные, клеевые и т.д.) Расчеты на прочность при сдвиге. Расчет из условий прочности на сдвиг используется при действии поперечных сил, например для различных соединений (заклепочные, сварные, клеевые, резьбовые и т.д.) Заклепочное соединение Используя условие *, получим: Поперечная сила равна Q=P, площадь сечения – площадь заклепки.
Сварное соединение
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 720; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |


 (Данная задача один раз статически неопределима)
(Данная задача один раз статически неопределима) (∆ может равняться 0; если ∆≥1,5, то задача статически определимая).
(∆ может равняться 0; если ∆≥1,5, то задача статически определимая).
 Определение внутренних сил:
Определение внутренних сил:

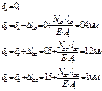
 стержень не может свободно деформироваться и, как следствие, возникают температурные напряжения. Здесь учитываются не только упругие деформации, но их совместное действие с температурным напряжением.
стержень не может свободно деформироваться и, как следствие, возникают температурные напряжения. Здесь учитываются не только упругие деформации, но их совместное действие с температурным напряжением. 
 (α- коэффициент линейного расширения)
(α- коэффициент линейного расширения) Геометрия
Геометрия 

 Физика
Физика 





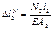

 Синтез
Синтез 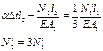
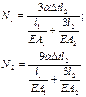

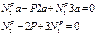 2.Геометрия
2.Геометрия 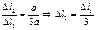 (см. прошлую задачу)
(см. прошлую задачу)

 4.
4. 
 (дополнительно нагружен первый стержень)
(дополнительно нагружен первый стержень)

 Q – перерезывающая сила.
Q – перерезывающая сила.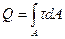 (1)
(1) . (2)
. (2)

 - абсолютный сдвиг (СС1=DD1)
- абсолютный сдвиг (СС1=DD1) ввиду малости
ввиду малости 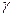 .
. (для растяжения
(для растяжения  )
)

 , где n количество заклепок.
, где n количество заклепок.




