Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б25: Основные кинематические и силовые соотношения в механических передачах.Содержание книги
Поиск на нашем сайте
Понятие о геометрических и кинематических характеристиках механизмов. Функцией положения механизма называется зависимость углового или линейного перемещения точки или звена механизма от времени или обобщенной координаты. Геометрические и кинематические характеристики механизма
Рис. 3.1 Кинематическими передаточными функциями механизма называются производные от функции положения по обобщенной координате. Первая производная называется первой передаточной функцией или аналогом скорости (обозначается Vq,wq), вторая - второй передаточной функцией или аналогом ускорения (обозначается aq, eq). Кинематическими характеристиками механизма называются производные от функции положения по времени. Первая производная называется скоростью (обозначается V, w), вторая - ускорением (обозначается a, e). Механизм с одной подвижностью имеет одно заданное входное движение и бесчисленное множество выходных (движение любого звена или точки механизма). Передаточные функции тех движений, которые в данном случае используются как выходные, называются главными, остальные - вспомогательными. Рассмотрим схему механической системы образованной последовательно-параллельным соединением типовых механизмов. Схема включает входное звено, зубчатую передачу, кулачковый и рычажный механизмы и имеет два выходных звена. Схема механической системы
Рис. 3.2
Рис. 3.3 Функции положения в механизмах
Методы геометро-кинематического исследования механизмов планов положений, скоростей и ускорений, проекций векторного контура, кинематических диаграмм, центроид, преобразования координат, экспериментальный, другие. Связь кинематических и передаточных функций Линейные скорости и ускорения
Угловые скорости и ускорения
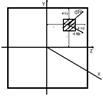
Так как данные формулы получены как производные от скалярных величин, то при операциях с векторными величинами они применимы только для проекций этих величин на оси координат. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ Напряженное состояние в точке. Используя метод сечения можно увидеть, что на отсеченной площадке, в общем случае, усилия распределяются произвольно, но в силу малости площадки dA, можно считать, что внутренние силы приложенные к ее различным точкам одинаковы по величине и направлению. Тогда равнодействующая этих сил dR будет проходить через центр площадки, с координатами y и z, и иметь проекции: dN – нормальная элементарная продольная сила, dQy и dQz – элементарные поперечные проекции равнодействующей. Тогда отношение Напряжение – это интенсивность соответствующих сил, действующих на элементарной площадке в соответствующей точке. Напряжение является мерой внутренних сил. В каждой точке тела при равенстве внешних и внутренних сил, имеет место напряженное состояние, которое характеризуется соотношением нормальных и касательных напряжений. Величина и направление напряжений зависит от ориентации площадки. Через любую точку можно провести бесконечное количество сечений. Однако есть такое положение, когда касательных напряжений не будет. Такие площадки называются главными, а соответствующие напряжения в этих площадках называются главными напряжениями. В зависимости от величины главных напряжений рассматриваются три напряженных состояния: 1. Линейное напряженное состояние σ1 >>σ2 σ1 >>σ3 (рис.1) 2. Плоское напряженное состояние σ1 ~σ2 σ1 >>σ3 σ2 >>σ3 (рис.2) 3. Объемное напряженное состояние
КИНЕМАТИКА 1. Основные вида движения твердого тела Понятия и определения Это раздел механики, в котором изучаются геометрические свойства движения тел, без учета действующих на них сил. Основными параметрами движения являются траектория скорость и ускорение. Закон движения устанавливает положение точки в пространстве, в зависимости от времени. В декартовой прямоугольной системе координат закон движения точки может быть представлен в следующем виде:
Модуль скорости определяется как геометрическая сумма его составляющих
Ускорение – вторая производная по времени от перемещения. Модуль ускорения определяется аналогично с модулем скорости:
Направляющие косинусы:
Все вышеизложенное относится к прямолинейному движению. При движении тела по траектории, отличающейся от прямой, выделяются касательные и нормальные составляющие ускорения. Касательные (тангенциальные) составляющие ускорения сонаправлены, или противоположно направлены вектору скорости и определяют изменение его модуля. Нормальные составляющие ускорения перпендикулярны вектору скорости и определяют изменение направления вектора скорости. Полное ускорение, с учетом этих составляющих:
Вращательное движение: Угол поворота вокруг оси есть функция времени: Угловая скорость: Угловое ускорение: Связь параметров поступательного и вращательного движений.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.102.79 (0.007 с.) |

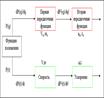

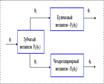
 Рис. 3.4
Рис. 3.4
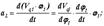

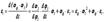
 будем называть нормальным напряжением,
будем называть нормальным напряжением, 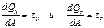 - касательными напряжениями.
- касательными напряжениями.


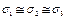 Напряжения соизмеримы между собой (рис.3).
Напряжения соизмеримы между собой (рис.3). 
 Проекции скорости на координатные оси равны первой производной от соответствующих перемещений по времени.
Проекции скорости на координатные оси равны первой производной от соответствующих перемещений по времени. . Для определения направления вектора скорости необходимо вычислить направляющие косинусы, из приведенных ниже уравнений:
. Для определения направления вектора скорости необходимо вычислить направляющие косинусы, из приведенных ниже уравнений: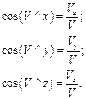
 .
.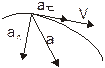

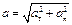

 .
.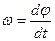 .
. .
.