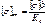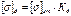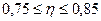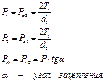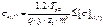Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б46: Основы кинетостатики. Принцип Даламбера.Содержание книги
Поиск на нашем сайте Основы кинетостатики Принцип Даламбера Пусть материальная точка М совершает движение с ускорением. На эту точку действует сила F= Для данной системы запишем условие равновесия, с учетом силы инерции.
Тогда сила инерции определится как:
Принцип: Если к действующим на точку активным силам и реакциям добавить силу инерции, то в каждый момент времени полученная система сил будет уравновешена. Принцип Даламбера представляет собой формальный математический прием, удобный для решения задач динамики. Этот прием позволяет записывать динамические уравнения движения в форме уравнений равновесия. Особенности: При криволинейном движении:
где Принцип Даламбера может быть записан и для моментов сил:
В механике макрообъектов внутренние силы считаются уравновешенными, и с учетом этого можем считать:
Можно принять, что силы и моменты инерции, представляются главным вектором и главным моментом сил инерции:
В проекциях на оси координат получают уравнения, аналогичные уравнениям статики: Для пространственной системы:
Для плоской системы:
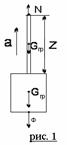
Расчеты при динамических нагрузках. Если известны действующие силы и силы инерции, возможно использование метода сечений и уравнения равновесия. Силы инерции вызывают в элементах конструкции дополнительные нагрузки и соответствующие напряжения. Для простоты эти напряжения можно считать статическими, но вызванными силами инерции. Для решения задач прочности связанными с динамическими нагрузками: 1. Определение ускорения точек; 2. Определение сил инерции; 3. Элемент (конструкция) нагружается силами инерции и внешними силами; 4. Расчеты ведутся по аналогии с расчетом статических систем. Пример: Требуется определить напряжение в тросе на расстоянии z от его конца. (Рис. 1).
 - объемный вес материала троса, А – площадь поперечного сечения троса. - объемный вес материала троса, А – площадь поперечного сечения троса. 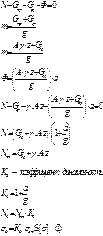
Б47: Червячные передачи. Усилия в зацеплении. Основы расчета на прочность. Червячные передачи. Червячная передача относится к числу так называемых зубчато-винтовых, т. е. имеющих признаки, характерные и для зубчатых, и для винтовых передач. Основные достоинства червячной передачи, обусловившие ее широкое распространение в различных отраслях машиностроения: 1. Плавность и бесшумность работы; 2. Возможность получения больших передаточных чисел при 3. Компактность. Недостатки червячной передачи: 1. Сравнительно невысокий к. п. д. 2. Сильный нагрев передачи вследствие перехода потерь на трение в тепловую энергию. Для уменьшения нагрева в червячной 3. Небольшие передаваемые мощности. Червячные передачи различают по числу заходов червяка — одно-, двух-, трех- и многозаходные; по расположению вала червяка — относительно червячного колеса с верхним, нижним и боковым расположениями. Усилия, действующие в зацеплении
d1,d2 – делительные диаметры червяка и колеса соответственно. Особенности расчета червячных передач Проектный расчет на контактную прочность строится на основе определения межосевого расстояния
Проверочный расчет на изгиб 1,2 – коэффициент упрочнения зуба за счет его длины и дугообразности.
у – коэффициент формы зуба.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |

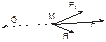
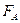 и равнодействующая сил реакции связи R. Добавим силу инерции точки М - Ф.
и равнодействующая сил реакции связи R. Добавим силу инерции точки М - Ф.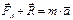 .
.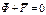
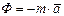
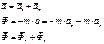 Для системы внешних и внутренних сил, принцип Даламбера может быть представлен в следующем виде:
Для системы внешних и внутренних сил, принцип Даламбера может быть представлен в следующем виде: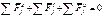 (1)
(1)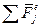 - сумма внешних сил,
- сумма внешних сил, 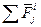 - сумма внутренних сил,
- сумма внутренних сил, 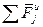 - сумма сил инерции.
- сумма сил инерции.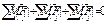 . (2)
. (2)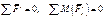
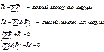
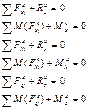
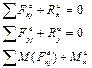
 Допускаемое напряжение с учетом зависимости (1) может быть представлено в следующем виде:
Допускаемое напряжение с учетом зависимости (1) может быть представлено в следующем виде: