
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б3: Гипотезы сопротивления материалов.Содержание книги
Поиск на нашем сайте
Методические основы. Определение внутренних сил и напряжений. (СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ) Метод сечений Процесс деформации тела под действием сил приводит либо к разрушению, либо к недопустимым искажениям изначальных размеров и форм конструкции. Правильный выбор материала, с учетом действия сил и условий эксплуатации, является основой науки о сопротивлении материалов. Сопротивление тел внешним силам обусловлено действием внутренних сил. Под действием внешних сил изменяются и внутренние силы. Величина внутренних сил может быть определена с помощью метода сечений. Сущность метода сечений: 1. Тело условно рассекается на две части. 2. Условно отбрасывается одна из частей. 3. Действие отброшенной части заменяется действием внутренних сил. 4. На оставшуюся часть действует система сил, которую можно привести к главному вектору и главному моменту. Главный вектор и главный момент раскладывают на координатные составляющие, и с их учетом, решается система уравнений равновесия, при этом можно выделить следующие факторы:
Qy и Qz - поперечные силы, вызывающие деформацию сгиба;
Б3: Гипотезы сопротивления материалов. Основные гипотезы и допущения сопротивления материалов. Основные гипотезы и допущения сопротивления материалов распространяются на свойства материалов, свойства нагрузок и характер деформаций. Гипотезы: 1. О сплошном строении тела. Эта гипотеза предусматривает, что тело не содержит пустот. 2. Об идеальной упругости материалов. Предусматривает, что после снятия нагрузки форма тела полностью восстанавливается до начальной. (рис.4)
3. Об изотропности материалов. Изотропность – одинаковость свойств во всех направлениях. 4. Об однородности материалов. Предусматривает независимость свойств материала от размеров и конфигурации материалов. 5. Плоских сечений. Предусматривает, что сечение является плоским и нормальным к оси бруса до и после нагружения. (рис.5) Допущения: 1. (6.) О малости деформации. Деформация очень мала по сравнению с размерами детали и не вызывает перераспределения нагрузки. 2. (7.) О линейной зависимости между деформацией и нагрузкой (выполнение закона Гука). Принципы: 1. (8.) Независимости действия сил (суперпозиции) Деформация или напряжение, вызванное различными факторами, могут быть определены как сумма действия этих факторов в отдельности. 2. (9.) Сен-Венана. Если тело нагружено статически эквивалентными силами, и размеры их области приложения не велики, то в сечениях, достаточно удаленных от мест приложения этих сил, напряжения не зависят от способа нагружения.
Б4: Геометрические характеристики плоских сечений. Б5: Механические свойства конструкционных материалов при растяжении и сжатии. Растяжение и сжатие. Механические характеристики материалов По механическим характеристикам материалы можно условно разделить на пластичные и хрупкие. По механическим характеристикам материалов, к которым относятся: предельные напряжения, ударная вязкость, твердость и т.д., определяется работоспособность механических деталей машин и приборов. Теоретически рассчитать механические свойства материалов затруднительно, поэтому эти свойства изучают экспериментально. Наиболее общий способ испытаний – растяжение и сжатие. При этом все материалы делятся на пластичные (например стали) и хрупкие (например чугун). Эти испытания проводятся в специальных машинах и прессах. Пластичные материалы могут деформироваться до 300% (фторопласт). Сталь может деформироваться без разрушения примерно на 5%. Диаграмма в координатах
I – участок пропорциональности (участок, на котором выполняется закон Гука;
II – на отрезке АВ сохраняется упругость материала; на ВС появляются пластические (необратимые) деформации; на СD – реализуется текучесть материала, которая характеризуется тем, что деформация изменяется, практически вне зависимости от нагрузки; III – участок упрочнения материала: происходит уплотнение структуры (для пластмасс реализуется ориентация макромолекул); IV – участок накопления повреждений, который заканчивается разрушением образца.
Используя диаграмму растяжений, рассмотрим предельные характеристики материалов:
Для хрупких материалов практически не реализуется закон Гука, и вид диаграммы может быть следующим. На этой диаграмме выделяют условный предел текучести, который определяют, как 0,2% от деформации образца. Растяжение и сжатие. Напряжение и перемещение. Р – продольная сила; l – продольный размер бруса; а – поперечный размер бруса;
Для большинства материалов влияние одной деформации на другую ограничено. Коэффициент Пуассона В случае растяжения, из имеющейся зависимости Экспериментально установлено, что при малых деформациях для большинства твердых тел имеет место прямая пропорциональность между нагрузкой и абсолютной деформацией.
Е – модуль упругости первого рода (модуль Юнга) характеризует упругие свойства материалов. Если возьмем зависимости 1 и 2 и подставим в 3, то получим:
Другими словами, абсолютное удлинение прямо пропорционально внутренней силе действующей на отрезке равном l, и обратно пропорционально площади сечения этого бруса и упругим свойствам материала, из которого изготовлен брус.
Особенности построения эпюр 1Скачки значений на эпюре внутренних сил определяются (или равны) внешними силами, приложенными в этой точке. 2Скачки эпюр на эпюре напряжений определяются изменением, как внешних сил, так и изменением размеров сечений. 3Эпюры напряжений, в данном случае, являются производной от эпюр перемещений. Сдвиговая деформация Основы Под сдвиговой деформацией понимается такой вид деформации, когда в поперечном сечении балки действует только перерезывающая сила. При «чистом» сдвиге на гранях выделенного из бруса элемента действуют только касательные напряжения, и такие грани называются гранями «чистого» сдвига. (Рис.1)
При равномерном распределении касательных напряжений выражение (1) упрощается:
При расчете на сдвиг (срез) условия прочности с учетом зависимости (2) записываются в следующем виде:
Рассмотрим рис.2 Грань CD под действием касательных напряжений смещается относительно грани АВ и при этом мы получаем
Угол В пределах упругости выполняется закон Гука для сдвиговых деформаций (напряжение пропорционально относительным деформациям).
Здесь G – модуль сдвига, как и при растяжении, он характеризует упругие свойства материала при сдвиговых деформациях (модуль второго рода). С учетом коэффициента Пуассона можно представить соотношение между модулем второго и первого рода.
Заключение: Расчет из условий прочности на сдвиг используется при действии поперечных сил для различных соединений (заклепочные, сварные, клеевые и т.д.) Расчеты на прочность при сдвиге. Расчет из условий прочности на сдвиг используется при действии поперечных сил, например для различных соединений (заклепочные, сварные, клеевые, резьбовые и т.д.) Заклепочное соединение Используя условие *, получим: Поперечная сила равна Q=P, площадь сечения – площадь заклепки.
Сварное соединение
Пример решения задач на кручение 1.Статически определимая 1.Определение внешнего крутящего момента Т1 (из условия равновесия) Т1=Т2+Т3+Т4=6*103 Н*м 2.Определение крутящих моментов действующих в сечении вала. (как внутренний силовой фактор) ТAB= -Т2= -2,7*103 Н*м ТBC= -Т2+Т1=3,3*103 Н*м ТCD= -Т2+Т1+Т3=1,3*103 Н*м 3.Определение диаметра вала из условия прочности
4. определение диаметра вала из условия жесткости
5.Принимаем, что φА=0
Дано: Т3=2*103 Н*м Т4=1,3*103 Н*м G=8*104 МПа [Θ]=0,25 °/м 1.Определение внешнего крутящего момента Т1 (из условия равновесия) Т1=Т2+Т3+Т4=6*103 Н*м 2.Определение крутящих моментов действующих в сечении вала. (как внутренний силовой фактор) ТAB= -Т2= -2,7*103 Н*м ТBC= -Т2+Т1=3,3*103 Н*м ТCD= -Т2+Т1+Т3=1,3*103 Н*м 3.Определение диаметра вала из условия прочности
5.Принимаем, что φА=0
Дано: Т=2*103 Нмм а=1м d=100мм G=8*104МПа Требуется построить эпюры Тх и φх. Решение: 1.Статика ТА-Т1+ТС=0 –уравнение равновесия, одно уравнение с двумя неизвестными (система статически неопределима). 2.Геометрия φAB+ φBC=0 углы закручивания. 3.Физика
4.TAB=TA TBC=TA-T
3TA-2T=0
TAB= -TA=8*103 Нм ТBC=TA-T= -4*103 Нм 6.Определение углов закручивания φА=0
Поперечный изгиб Чистый изгиб и его особенности Брусья, работающие на изгиб, называются балками.
Прямым поперечным изгибом называется изгиб, когда внешняя сила перпендикулярна продольной оси балки и проходит через ось симметрии. (Сила Р вызывает прямой поперечный изгиб, а сила Р1 – косой изгиб). Косой изгиб реализуется, когда силы образуют угол с плоскостью симметрии величиной отличающейся от В поперечных сечениях балки при изгибе возникают два внутренних фактора: поперечные силы и изгибающие моменты. Если поперечная сила равна нулю, и действует только изгибающий момент, то такой изгиб называют чистым изгибом. Допущения 1. Плоские поперечные сечения остаются плоскими и поворачиваются на некоторый равный угол, одно относительно другого, при действии изгибающего момента. 2. Плоские продольные сечения искривляются. 3. Слои на вогнутой стороне балки сжимаются, а на выгнутой – растягиваются. Нейтральный слой не изменяет своей длины, а следовательно является ненагруженным. Определение внутренних силовых факторов. Внутренние силовые факторы: - внутренняя сила, - изгибающий момент, зависят от внешней нагрузки и изменяются по длине балки. Для составления уравнений, определяющих значения и, и построения соответствующих эпюр, принимают следующий правила: рис.1 Для изгибающих моментов: Если балка изгибается под действием моментов выпуклостью вниз, то внутренний силовой фактор – момент, действующий в данном сечении балки, принято считать положительным и наоборот; если изгиб происходит выпуклостью вверх, то момент, действующий в сечении балки, будет отрицателен. Для поперечных сил: Поперечная сила будет положительна, если внешние силы стремятся приподнять левую часть балки относительно правой, или опустить правую часть балки относительно левой, и наоборот. Определение значений: Поперечные силы: Поперечная сила определяется как алгебраическая сумма сил, расположенных по одну сторону от данного сечения. Изгибающие моменты: Изгибающий момент в любом сечении балки равен алгебраической сумме моментов внешних сил, действующих по одну сторону от данного сечения. q – распределенная сила.
2) Определение поперечной силы, действующей в сечении х.
3)Определение изгибающего момента, действующего в сечении х.
Теорема Журавского (для Рис.3)
Нормальные напряжения при изгибе. Нормальные напряжения при изгибе вызываются изгибающим моментом, действующим в данном сечении. В соответствии с законом Гука Относительное удлинение при растяжении, которое реализуется, входе деформации изгиба - Дуга рис.2 Тогда закон Гука примет вид
Касательные напряжения при изгибе вызванные действием поперечных сил. рис.1
Касательное напряжение - функция статического момента площади. с учетом (2) A=b(h/2-y) (3)
с учетом (3) и (4)
Рассмотрим граничные условия: При y=h/2 S=0 τ=0 y=-h/2 s=0 τ=0 y=0 Для сложных форм сечения фигуру разбивают на отдельные части и рассчитывают суммарный статический момент площади поэлементно.
Расчеты на прочность при изгибе Рассмотрим различные напряженные состояния и возможные условия прочности. 1. В точках 1 и 4 касательные напряжения равны нулю, а нормальные напряжения максимальны и могут быть определены зависимостью 2. точка 3. Нормальные напряжения равны нулю, касательные напряжения максимальны и определяются уравнением:
1. точка 2.
В соответствии с третьей теорией прочности Условие прочности для хрупких материалов:
Сложное сопротивление. Теория прочности. Сложное сопротивление возникает тогда, когда в поперечном сечении бруса действуют несколько иловых факторов. Для сложного сопротивления выработаны теории, критерии (гипотезы) прочности, о преимущественном влиянии какого-либо из факторов. При этом, фактическое напряженное состояние заменяется эквивалентным линейным состоянием, которые приводятся к нормальным эквивалентным напряжениям. 1. Теория наибольших нормальных напряжений Принимается, что прочность зависит от величины наибольшего нормального напряжения.
Данная теория для пластичных материалов не подтверждается, но удовлетворительно работает при оценке прочности при растяжении для хрупких материалов. 2. Теория набольших линейных деформаций. Согласно этой теорией причиной разрушения является наибольшая одноосная (линейная деформация).
С использованием обобщенного закона Гука:
Данный критерий подтверждается для хрупких материалов. 3. Теория наибольших касательных напряжений
Этот критерий находит наибольшее применение для эквивалентных напряжений, выраженных формулой:
4. Энергетическая теория. Согласно этой теории, предельное состояние определяется предельным значением энергии растяжения, с учетом действия всех трех главных напряжений. Этот критерий находит наибольшее применение для эквивалентных напряжений, выраженных формулой.
Данная теория хорошо согласуется с расчетами пластичных материалов. 5.Теория Мора
k – коэффициент, учитывающий различное сопротивление материалов растяжению и сжатию. Изгиб с кручением В качестве примера на изгиб с кручением может быть рассмотрена работа вала для передачи любого вращательного движения. d – диаметр вала. Крутящий момент, передаваемый этим колесом:
Расчетная схема действия крутящих моментов:
рис.1 Изгибающий момент вызывает нормальное напряжение на этом валу.
Крутящие моменты вызывают касательные напряжения.
Используем третью теорию (теорию наибольших касательных напряжений) в виде:
При помощи вышеприведенного уравнения можно решать основные задачи сопротивления материалов применительно к изгибу с кручением. Задача Эйлера. Заключается в нахождении критической нагрузки.
пусть
при x=l/2
Вводя коэффициент μ-коэффициент определяющий форму заделки:
Формула Эйлера справедлива лишь в пределах пропорциональности т.е. когда работает закон Гука. Б20: КПД сложных систем. Механический коэффициент полезного действия Работа сил терния затрачивается на нагревание и износ кинематических пар. В общем случае баланс работ для любого механизма определяется работой движущих сил, минус работа полезного сопротивления, минус работа сил трения.
Коэффициент полезного действия оценивает полезную используемую энергию.
При холостом ходе КПД равен нулю. Аналогично можно определить коэффициент потерь Определение КПД для сложных систем. Последовательное соединение механизмов. Для всей этой системы можно записать:
рис.1
Пусть КПД пары подшипников равен Параллельное соединение механизмов.
Тогда КПД всей системы:
Детали машин. Понятия и определения. Систематика машин и механизмов. Машина – устройство, создаваемое для использования законов природы, с целью облегчения физического и умственного труда и увеличения его производительности. Встречаются машины следующих типов: 1.Машина-«Двигатель». Машины данного типа преобразуют различные типы энергии в механическую работу. 2.Машина-«Преобразователь». Данного типа машины, преобразуют механическую работу в различные виды энергии. 3.«Транспортная машина». Преобразуют механическую работу двигателя в механическую работу по перемещению. 4.«Технологические машины» используются для изменения свойств, размеров и состояния материалов, а также для сборочных процессов. 5.«Информационно-кибернетические машины» служат для восприятия, передачи, хранения и использования информации для управления различными процессами. Для большинства перечисленных машин может быть дана следующая структурная схема:
Привод машин (может быть пневматическим, механическим и т. д.) Д- двигатель. ПМ- передаточный механизм. ИМ- исполнительный механизм. Механические передачи Механические передачи – устройства для передачи энергии от источника к потребителю с изменением угловой скорости, крутящего момента, вида движения. Механические передачи входят в состав машин. Необходимость использования передаточных механизмов возникает когда: 1) угловые скорости валов ИМ (исполнительного механизма) отличаются от угловых скоростей валов двигателя, при этом требования к ИМ (например, по величине угловой скорости), как правило, нецелесообразно переносить на двигатель, так как мощность и КПД двигателя уменьшается, а стоимость двигателя увеличивается, если эти требования реализовать в двигателе; 2) необходимо преобразовать один вид движения в другой; 3) необходимо передать движение сразу к нескольким ИМ с различными кинематическими характеристиками и видами движения. Основы классификаций механических передачСборочные единицы и детали машин и механизмов.
Сборочными единицами могут быть подшипники, червячное колесо в сборе, уплотнительные устройства, измерители уровня масла, различные соединения (разъемные, неразъемные: сварные, заклепочные, клеевые). Детали машин: оси, валы, колеса, корпусные детали, рамы, опоры валов (подшипники качения). Зубчатые передачи. Общие характеристики. Зубчатые передачи служат, как правило, для передачи вращательного движения. В некоторых случаях их применяют для преобразования вращательного движения в поступательное, и наоборот. Зубчатые передачи отличаются широким диапазоном скоростей (0÷100 м/с) и широким диапазоном мощностей (от нескольких Ват до десятков тысяч кВат). Основные достоинства и недостатки приведены в таблице №1. Табл. №1.
Динамика точки и системы. Дифференциальное уравнение движения материальной точки. Используя основной закон динамики можно рассмотреть дифференциальное уравнение материальной точки.
Пусть равнодействующая всех сил и реакций связи будет
Тогда: Соответственно в декартовой системе координат:
Выражая проекции ускорения через вторые производные по перемещению, получаем:
Дифференциальное уравнение материальной точки в декартовой системе координат, в конечном счете, примет следующий вид:
Рассмотрим один из примеров: (Рис. 2) Груз весом Р начинает движение из состояния покоя вдоль гладкой горизонтальной плоскости, под действием силы F:
Найти закон движения груза. Решение: Н.У: t=0, x=0, Vx=0, m=P/g. Используем выражения (2).
После интегрирования получим:
Подставив начальные условия, получаем:
Следовательно, окончательное выражение для перемещения примет вид:
Опоры и направляющие. Опорами и направляющими называются устройства, обеспечивающие вращательное движение частей механизмов. Различаются опоры скольжения, опоры качения, опоры с упругими элементами, опоры с газовой смазкой, опоры с магнитными подвесами. Наибольшее распространение получили опоры качения. Опоры скольжения. Основы классификации. Достоинства подшипников трения-качения. 1. Малые моменты сопротивления при троганьи; 2. малые потери на трение; 3. простота сборки и ремонта механизма; 4. малые осевые габариты. Недостатки подшипников трения-качения. 1. повышенная чувствительность к ударным и вибрационным нагрузкам; 2. повышенные радиальные габариты. Подшипники скольжения делятся: 1. на стандартные и насыпные 2. по способности воспринимать нагрузку а) по направлению - радиальные, радиально-упорные и упорные. б) по величине – сверхлегкая, легкая, средняя, тяжелая и др. серии. 3. по форме тел качения – шариковые, роликовые (цилиндрические, конические, бочкообразные, игольчатые). 4. по конструктивно-эксплуатационным признакам: (не) самоустанавливающиеся, (не) разборные.
Размер: 00-10 мм 01-12 мм 02-15 мм 03-17 мм 04-20 мм далее кратные 5 Серии: 1 – особо легкая 2 - легкая 3 - средняя 4 – тяжелая Типы тел качения: 0 –шариковые; 1 –шариковые двухрядные; 2 – радиальные с короткими роликами; 7 – упорно-шариковые. Наибольшее распространение получили радиальные шариковые подшипники (0), которые могут воспринимать как радиальные, так и небольшие осевые нагрузки. Цилиндрические роликовые могут выдерживать по сравнению с шариковыми большие радиальные нагрузки, но не выдерживают осевых. Подшипники с витыми роликами за счет упругих деформаций ролика выдерживают ударные нагрузки. Игольчатые подшипники находят применение в тяжелонагруженных тихоходных передачах, отличаются малыми габаритами в радиальном направлении. Конические роликовые подшипники используются как радиально-упорные, для восприятия радиальных и односторонних осевых нагрузок. Упорные подшипники – воспринимают односторонние осевые нагрузки. Тела качения в этих подшипниках могут быть и в виде шариков и в виде роликов. Выбор и основы расчета подшипников качения. Долговечность подшипников качения ограничивается усталостным выкрашиванием поверхностных слоев дорожек качения. При радиальных нагрузках устанавливаются радиальные подшипники, это реализуется, например, для цилиндрических прямозубых передач. При сочетании радиальных и осевых нагрузок устанавливаются, как правило, радиальноупорные подшипники (используются в цилиндрических косозубых, конических и червячных передачах). При частоте вращения внутреннего кольца подшипников больше чем 1 об/мин подбор подшипников осуществляется по динамической грузоподъемности (С), в противном случае по статической грузоподъемности (С0). Динамическая грузоподъемность для радиальных и радиально-упорных подшипников определяется такой радиальной нагрузкой, при которой группа идентичных под
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 381; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.81 (0.017 с.) |

 Критериями работоспособности, с позиции механики, являются: прочность (способность материала сопротивляться разрушению), жесткость (- характеристика элемента конструкции, определяющая его способность сопротивляться деформации (растяжению, изгибу, кручению и т.д.); зависит от геометрических характеристик сечения и физических свойств материала (модулей упругости)), устойчивость (способность механической системы сохранять первоначальные условия равновесия).
Критериями работоспособности, с позиции механики, являются: прочность (способность материала сопротивляться разрушению), жесткость (- характеристика элемента конструкции, определяющая его способность сопротивляться деформации (растяжению, изгибу, кручению и т.д.); зависит от геометрических характеристик сечения и физических свойств материала (модулей упругости)), устойчивость (способность механической системы сохранять первоначальные условия равновесия). - продольная сила, которая вызывает деформацию растяжения – сжатия;
- продольная сила, которая вызывает деформацию растяжения – сжатия;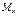 - крутящий момент, вызывающий деформацию кручения;
- крутящий момент, вызывающий деформацию кручения; и
и  - моменты, вызывающие деформацию изгиба.
- моменты, вызывающие деформацию изгиба.

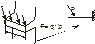

 называется машинной и зависит от размеров образца, поэтому ее заменяют условной диаграммой в координатах
называется машинной и зависит от размеров образца, поэтому ее заменяют условной диаграммой в координатах  , в которой нет этой зависимости.
, в которой нет этой зависимости.

 - предел пропорциональности;
- предел пропорциональности; - предел упругости в точке В;
- предел упругости в точке В;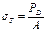 - предел текучести;
- предел текучести; - предел временного сопротивления в точке М.
- предел временного сопротивления в точке М.
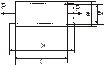
 - абсолютное удлинение;
- абсолютное удлинение; - абсолютное сужение бруса.
- абсолютное сужение бруса. (1) - относительная продольная деформация (удлинение);
(1) - относительная продольная деформация (удлинение); - относительная поперечная деформация;
- относительная поперечная деформация; показывает взаимное влияние продольной и поперечной деформации друг на друга. При этом для большинства материалов
показывает взаимное влияние продольной и поперечной деформации друг на друга. При этом для большинства материалов  .
. , можно записать, при А=const,
, можно записать, при А=const, 
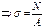 (2).
(2). - закон Гука (3)
- закон Гука (3)

 Q – перерезывающая сила.
Q – перерезывающая сила.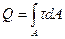 (1)
(1) . (2)
. (2)

 - абсолютный сдвиг (СС1=DD1)
- абсолютный сдвиг (СС1=DD1) ввиду малости
ввиду малости 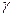 .
. (для растяжения
(для растяжения  )
)

 , где n количество заклепок.
, где n количество заклепок.

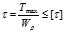
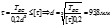
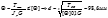 Анализируя результаты мы можем считать что более жестким является условие жесткости, тогда принимаем d=100мм
Анализируя результаты мы можем считать что более жестким является условие жесткости, тогда принимаем d=100мм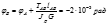
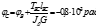
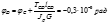 Пример решения статически неопределимой задачи.
Пример решения статически неопределимой задачи.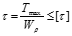
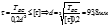 4. определение диаметра вала из условия жесткости
4. определение диаметра вала из условия жесткости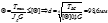 Анализируя результаты мы можем считать что более жестким является условие жесткости, тогда принимаем d=100мм
Анализируя результаты мы можем считать что более жестким является условие жесткости, тогда принимаем d=100мм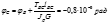
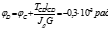 Пример решения статически неопределимой задачи.
Пример решения статически неопределимой задачи.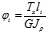
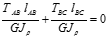 TA*a+(TA-T)2a=0
TA*a+(TA-T)2a=0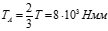
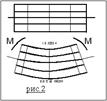 5.Определение крутящих моментов действующих в сечении вала.
5.Определение крутящих моментов действующих в сечении вала.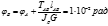
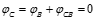
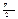 , и проходят через ось балки.
, и проходят через ось балки.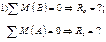

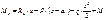
 В соответствии с теоремой Журавского, поперечная сила является производной от момента, действующего в сечении, на расстоянии х.
В соответствии с теоремой Журавского, поперечная сила является производной от момента, действующего в сечении, на расстоянии х. ,
, .
.
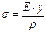 .
.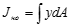
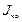 - момент инерции относительно нейтральной оси
- момент инерции относительно нейтральной оси
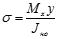
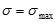 если
если 

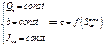
 (4)
(4)

 ≤[σ]
≤[σ]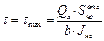

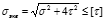
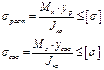 , где
, где  - расстояние до растягивающихся или сжимаемых волокон.
- расстояние до растягивающихся или сжимаемых волокон. в данном случае
в данном случае  - наибольшее главное напряжение.
- наибольшее главное напряжение. ≤[ε]
≤[ε] Умножив левую и правую часть на модуль упругости, получим:
Умножив левую и правую часть на модуль упругости, получим: В этом случае учитываются три главных напряжения.
В этом случае учитываются три главных напряжения.
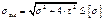

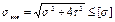 Данная теория удовлетворительна для пластичных материалов.
Данная теория удовлетворительна для пластичных материалов.
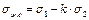 ≤[σ]
≤[σ]
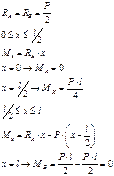




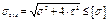


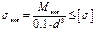 - условие прочности для изгиба с кручением.
- условие прочности для изгиба с кручением.
 описываем у синусоидой
описываем у синусоидой Проинтегрировав, получим
Проинтегрировав, получим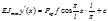 при x=l/2
при x=l/2 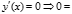
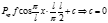
 при x=0
при x=0 
 (*)
(*)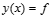
 - формула Эйлера.
- формула Эйлера.
 .
. <1 из-за Amp (1)
<1 из-за Amp (1) .
.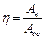

 рис.2
рис.2 

 , а КПД зубчатых колес
, а КПД зубчатых колес 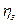 , в данном случае (см. рисунок) КПД системы будет равен
, в данном случае (см. рисунок) КПД системы будет равен 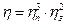 . (Рис. 2)
. (Рис. 2)

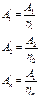


 , а масса m. Ускорение, в общем виде, можно выразить через радиус-вектор:
, а масса m. Ускорение, в общем виде, можно выразить через радиус-вектор: .
. .
.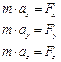




 - закон изменения линейной силы.
- закон изменения линейной силы.
 .
.

 .
.


