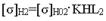Задачи сопротивления материалов

Сопротивление материалов представляет собой одно из направлений механики деформируемого твердого тела, которое под действием приложенных к нему сил изменяет свою форму и размеры — деформируется.

На основе методов сопротивления материалов и смежных областей механики деформируем ого тела (математической и прикладной теории упругости, математической и прикладной теории пластичности, статики и динамики сооружений) выполняют расчеты машин, аппаратов, приборов, конструкций промышленных и гражданских сооружений. Эти расчеты служат для обеспечения надежности и долговечности проектируемых конструкций при минимальной затрате материалов для их изготовления.

Для балки, показанной на рис. 1.1, методами статики абсолютно твердого тела может быть решена задача об определении реакции шарнирно-неподвижной опоры А и реакции тяги ВС, возникающих под действием приложенной к балке нагрузки (в нашем случае силы F). Эти реакции показаны на чертеже, реакция тяги ВС условно несколько смещена от оси тяги. Напомним, что тело называют абсолютно твердым (или абсолютно жестким), если независимо от приложенных к нему сил расстояние между любыми двумя точками тела остается неизменным. Реальные твердые тела под действием приложенных к ним сил деформируются; в рассматриваемом случае тяга удлинится, а балка изогнется примерно так, как показано штриховыми линиями на рис. 1.1.

Допустим теперь, что балка разгружена: сила F удалена. При этом в зависимости от силы F (силу тяжести конструкции не учитываем), материалов, размеров балки и тяги могут возникнуть два случая (конечно, полагаем, что при действии силы F ни один из элементов конструкции не разрушается).

1. Балка и тяга полностью восстанавливают те формы и размеры, которые они имели до нагружения; в этом случае говорят, что в системе (конструкции) при заданной нагрузке возникают лишь упругие деформации.

2. Деформации балки и тяги уменьшаются, но система все же остается в деформированном состоянии; такое положение означает, что в системе при заданной нагрузке возникают

наряду с упругими также и пластические (остаточные) деформации.

Как правило, возникновение пластических деформаций связано с нарушением нормальной работы конструкции и потому считается недопустимым.

Пусть, например, тяга, изготовленная из стального прутка, имеет круглое поперечное сечение, а балка (также стальная)— двутавровый профиль. При заданной силе F следует выбрать диаметр сечения тяги и номер двутаврового профиля балки, чтобы ни один из элементов конструкции не разрушился и в нем не возникли пластические деформации. При соблюдении указанных условий балка и тяга имеют достаточную прочность. Легко понять, что возможна и обратная постановка задачи: размеры и материалы балки и тяги известны и требуется определить то наибольшее значение силы F, при котором прочность конструкции обеспечена.

Из рассмотренного примера вытекает, что первая задача сопротивления материалов — расчет элементов конструкций на прочность. При этом подчеркиваем еще раз, что в сопротивлении 'материалов под нарушением прочности понимают не только разрушение в буквальном смысле слова — разрыв, излом, но и возникновение пластических (остаточных) деформаций.

Говоря о достаточной прочности конструкции, полагают, что прочность обеспечена не только при заданном значении нагрузок, но и при некотором их увеличении, т. е. конструкция имеет определенный запас прочности.

В конструкциях одноразового применения допустимо возникновение пластических деформаций. Для некоторых машин и аппаратов химических производств, а также в некоторых других случаях допускают возникновение небольших местных пластических деформаций, которые не являются признаком нарушения прочности. В кратком курсе сопротивления материалов расчеты, где учитывается развитие пластических деформаций, не рассматриваются.

Возникновение упругих деформаций в нагруженной конструкции неизбежно, также неизбежны и обусловленные этими деформациями перемещения отдельных точек конструкции, Так, в частности, в рассматриваемом примере конец балки по

лучает некоторое вертикальное перемещение f (рис. 1.1). Может оказаться, что значение /' больше допустимого по условиям нормальной работы конструкции, хотя ее прочность вполне достаточна. В эом случае говорят, что конструкция имеет недостаточную жесткость.

Вообще жесткостью называют способность материала нлн элемента конструкции сопротивляться упругим деформациям. Можно также сказать, что жесткостью конструкции называют ее способность воспринимать нагрузку без существенного изменения геометрических размеров. На рис. 1.2 показан пример, иллюстрирующий последствия недостаточной жесткости конструкции: значительные прогибы валов зубчатой передачи приводят к неравномерному распределению нагрузки по длине зубьев, что связано с повышенным износом и даже опасностью поломки зубьев.

Вторая задача сопротивления материалов — расчет элементов конструкций на жесткость.

Соответствующий расчет при проектировании конструкции должен обеспечить выбор таких ее размеров, при которых упругие перемещения, вызванные рабочими нагрузками, будут лежать в допустимых пределах.

Обратимся еще к одному примеру (рис. 1.3,а), отличающемуся от первого лишь тем, что здесь стержень ВС, поддерживающий балку, испытывает не растяжение, а сжатие. Если стержень ВС сравнительно длинный и тонкий, то при некоторой силе F он может внезапно изогнуться (выпучиться), как показано штриховыми линиями на рис. 1.3,б, или, как говорят, потерять устойчивость. В этом случае стержень ВС помимо сжатия будет испытывать так называемый продольный изгиб. Иными словами, при достижении нагрузкой критического значения первоначальная прямолинейная форма равновесия стержня становится неустойчивой и возникает новая устойчивая форма равновесия — криволинейная. При этом качественном изменении характера деформации конструкция практически выходит из строя: она или разрушается, или в ней возникают недопустимо большие перемещения (прогибы). Поэтому расчет конструкции должен обеспечить такое соотношение нагрузок, размеров и свойств материалов, при котором гарантирована (с определенным запасом) устойчивость заданной (прямолинейной) формы равновесия.

Итак, третья задача сопротивления материалов — расчет элементов конструкций на устойчивость.

Подводя итог всему сказанному выше, заключаем, что сопротивление материалов дает основы расчета элементов конструкций на прочность, жесткость и устойчивость.

Сопротивление материалов — расчетно-теоретическая дисциплина, основные положения которой проверяются и дополняются экспериментальными исследованиями. Опытная проверка теоретических расчетов и формул необходима потому, что они основаны на ряде упрощающих предпосылок и допущений. Эти предпосылки и допущения связаны как со свойствами материалов, так и с характером деформаций элементов конструкций. В ряде случаев приходится специально изготовлять модель проектируемой конструкции (или отдельных ее элементов) и подвергать ее испытаниям, чтобы получить данные о характере и величине деформаций, так как чисто теоретическим путем создание методов расчета оказывается вообще невозможным. Наконец, необходимо учесть, что все расчеты, выполняемые методом сопротивления материалов, базируются на знании физико-химических свойств конструкционных материалов. Эти свойства определяют путем лабораторных испытаний специально изготовленных образцов.

При решении задач сопротивления материалов широко применяют уравнения равновесия различных систем сил, полученные в статике абсолютно твердого тела. Вместе с тем не все приемы и методы статики могут быть использованы в сопротивлении материалов. Замена одной системы сил другой, статически эквивалентной, в частности перенос силы по линии ее действия и замена ряда сил их равнодействующей, резко изменяет характер деформации детали и поэтому недопустима. Поясним это положение некоторыми примерами.

На рис. 1.4, а, б показан брус, нагруженный растягивающей силой F; в первом случае сила приложена к концу бруса, во втором она перенесена по линии действия в некоторую точку В. В результате этого переноса деформироваться будет не весь брус, а только часть АВ.

Перенос сил по линиям их действия может привести к еще более резкому изменению характера деформации, чем в рассмотренном случае. Например, в результате переноса сил, приложенных к торцам бруса (рис. 1.5,и), можно получить нагружение, показанное на рис. 1.5, б, т. е. брус будет испытывать не растяжение, а сжатие.

На рис. 1.6,а изображена балка, нагруженная парой сил на левой опоре. Штриховой линией показан характер ее деформации. При переносе этой пары сил в положение, показанное на рис. 1.6,б, характер деформации резко изменяется. При втором положении нагрузки допускаемое по условию прочности значение момента пары вдвое больше, чем в первом. Реакции опор балки в том и другом случаях, конечно, одинаковы.

На рис. 1.7,а,б показаны две одинаковые балки, первая нагружена равномерно распределенной нагрузкой интенсивностью q, а вторая — силой F ф (т. е. силой, равной равнодействующей этой нагрузки). Опорные реакции рассматриваемых балок одинаковы, но наибольший прогиб второй балки в 1,6 раза больше, чем первой, а допускаемая по условию ее прочности нагрузка вдвое меньше.

Из рассмотренных примеров следует, что при определении опорных реакций в статически определимых системах статически эквивалентные преобразования нагрузки допустимы, но при вычислении перемещений и расчетах на прочность замена некоторой системы сил другой, статически эквивалентной заданной, приводит к весьма серьезным ошибкам.

Б23: Контактные напряжения. Основы расчета.++

Контактные напряжения, напряжения, которые возникают при механических взаимодействии твёрдых деформируемых тел на площадках их соприкасания и вблизи этих площадок (например, при сжатии соприкасающихся тел). Знание К. н. важно для расчёта на прочность подшипников, зубчатых и червячных передач, шариковых и цилиндрических катков, кулачковых механизмов и т. п.

К. н. быстро убывают при достаточном удалении от места контакта (соприкасания тел). Распределение К. н. по площадке контакта и в её окрестности неравномерно и характеризуется большими градиентами, причём максимальные касательные напряжения tmax, которые в значительной мере предопределяют прочность сжимаемых тел (например, при сжатии шаров или пересекающихся цилиндров), имеют место на некоторой глубине (точка А) под площадкой контакта. Вблизи самой этой площадки напряжённое состояние близко к гидростатическому сжатию, при котором, как известно, касательные напряжения отсутствуют.

Расчет допускаемых контактных напряжений

Расчет допускаемых контактных напряжений производят исходя из следующих предпосылок. Согласно графику усталостно-контактного нагружения в области малоцикловой контактной усталости существует обратно пропорциональная зависимость между величиной и количеством циклов до разрушения. Указанная тенденция сохраняется до тех пор, пока величина напряжения в контакте не снизится до значения предельного контактного напряжения. При этом материал может работать бесконечно долго.

Расчет допускаемых контактных напряжений проводят по следующим формулам:

(3.1)

(3.2)

где - допускаемые контактные напряжения для материала ведущей и ведомой шестерни соответственно, Мпа;

- предельные значения допускаемых контактных напряжений для материала ведущей и ведомой шестерни соответственно, Мпа.

= 1,8НВ+67= 1,8*290+67= 589МПа

= 1,8НВ+67= 1,8*250+67= 517Мпа

KHL1, KHL2 - коэффициенты долговечности для материала ведущей и ведомой шестерни соответственно.

Коэффициенты долговечности по своей сути позволяют дифференцированно подойти к шестерне и колесу с учетом их реальной нагрузки и числа циклов нагружения за весь период службы.

Коэффициенты долговечности можно рассчитать по формуле:

(3.3)

(3.4)

где NH01, NH02 - базовое количество циклов для материала ведущей и ведомой шестерни соответственно, цикл;

NH01= 20*106; NH02= 125*106;

NH1, NH2 - число циклов нагружения контактными нагрузками ведущей и ведомой шестерни соответственно.

NH1=Lh*n1*60*Kрев (3.5)

NH2=Lh*n2*60*Kрев (3.5)

где Lh - моторесурс (чистое время работы) проектируемой передачи, час;

n1, n2 - частоты вращения ведущей и ведомой шестерни соответственно, об/мин;

Kрев - коэффициент реверсивности, Kрев=1.

Моторесурс можно рассчитать по формуле:

Lh=Lгод*365*Кгод*24*Ксут*ПВ

где Lгод - число лет работы привода, Lгод=10;

Кгод - коэффициент годового использования, Кгод=РД/365,

РД - число рабочих дней в году, РД=200,

Кгод=200/365=0,55;

Ксут- коэффициент суточного использования, Ксут=РЧ/24,

РЧ - число часов работы в сутки, РЧ=8,

Ксут=8/24=0,33;

ПВ - коэффициент продолжительности включения в течение часа,

ПВ=РМ/60, РМ - число минут работы в час, РМ=60, ПВ=60/60=1.

Подставляя данные в (3.7), получим:

Lh=10*365*0,55*24*0,33*1=15899,4 часов.

Подставляя данные в (3.5), (3.6), получим:

NH1=15899,4*5,29*60*1,

NH1=15899,4*2,11*60*1.

Подставляя данные в (3.3), (3.4), получим:

 

Подставляя данные в (3.1), (3.2), получим: