Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б11: Кручение стержня круглого сечения. Напряжение и перемещение при кручении.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кручение Понятия и определения Цилиндрический брус, закрепленный одним концом и нагруженный парой сил с моментом Т, действующим в поперечном сечении этого бруса, претерпевает деформацию кручения (Рис.1) 1.Ось бруса (цилиндра) не деформируется; 2.Нормальные поперечные сечения остаются плоскими и нормальными к оси цилиндра после приложения момента сил (гипотеза плоских сечений); 3.Равноотстоящие поперечные сечения поворачиваются одно относительно другого на равные углы; 4.Угол поворота концевого сечения (φ-полный угол закручивания) относительно закрепления 5.При кручении цилиндра в его поперечном сечении возникают только касательные напряжения. Определения внутренних силовых факторов при кручении. При действии нескольких разнонаправленных крутящих моментов, крутящий момент в сечении численно равен алгебраической сумме внешних крутящих моментов, действующих слева, или справа от рассматриваемого сечения. Дано: вал – 1, в подшипниках 2. Вращаются три шкива. Все определено. Решение: за положительное направление выбираем положительное направление вращения часовой стрелки.
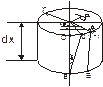
Напряжения и перемещения при кручении
r - полный радиус;
СС1 - абсолютный сдвиг на длине dx.
Согласно гипотезе плоских сечений, при кручении радиусы остаются прямыми, тогда зависимость относительного сдвига для произвольного радиуса можно записать в виде:
Только что рассмотренная формула показывает, что при кручении реализуется неравномерный сдвиг при Согласно закону Гука, для сдвиговой деформации касательные напряжения будут определяться из формулы:
при Поперечная сила может быть выражена через касательное напряжение:
dQ – элементарная поперечная сила. Элементарный крутящий момент, действующий на расстоянии
В сопротивлении материалов принято, что ∫ ρ2 dA= Jρ и является полярным момент инерции сечения (геометрическая характеристика сечения, которая учитывает и форму сечения).
Относительная деформация в сечении прямо пропорциональна действующему моменту в этом сечении, и обратно пропорциональна жесткости стержня (жесткость при кручении определяется как произведение модуля сдвига на полярный момент инерции). При равномерном распределении касательных напряжений
c учетом (***) Ранее была получена зависимость: c учетом (***) получим В соответствии с этой формулой можно оценить действующие касательные напряжения с учетом места и формы сечения.
Условие прочности при кручении
Условие жесткости при кручении может быть представлено следующим образом:
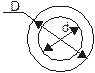
Полярные моменты инерции для круглого сечения Ранее была предложена зависимость:
Приближенная формула для определения полярного момента сопротивления плоского сечения
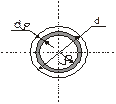
Для кольцевого сечения d – внутренний диаметр; D – внешний диаметр. Используя свойства интеграла, получим:
Б12: Расчеты на прочность и жесткость при кручении. Расчеты на прочность и жесткость при кручении. Для расчетов на прочность используются условия прочности и жесткости. Эти условия позволяют решать основные типы задач сопротивления материалов (проверочные, проектные, задачи на определение несущей способности). Особенности решения статически неопределимых систем, при кручении, заключаются в том, что известные алгоритмы решении рассматриваются с позиции совместных перемещений, при кручении, в соответствии с законом Гука и использованием выражения:
Пример решения задач на кручение 1.Статически определимая 1.Определение внешнего крутящего момента Т1 (из условия равновесия) Т1=Т2+Т3+Т4=6*103 Н*м 2.Определение крутящих моментов действующих в сечении вала. (как внутренний силовой фактор) ТAB= -Т2= -2,7*103 Н*м ТBC= -Т2+Т1=3,3*103 Н*м ТCD= -Т2+Т1+Т3=1,3*103 Н*м 3.Определение диаметра вала из условия прочности
4. определение диаметра вала из условия жесткости
5.Принимаем, что φА=0
Дано: Т3=2*103 Н*м Т4=1,3*103 Н*м G=8*104 МПа [Θ]=0,25 °/м 1.Определение внешнего крутящего момента Т1 (из условия равновесия) Т1=Т2+Т3+Т4=6*103 Н*м 2.Определение крутящих моментов действующих в сечении вала. (как внутренний силовой фактор) ТAB= -Т2= -2,7*103 Н*м ТBC= -Т2+Т1=3,3*103 Н*м ТCD= -Т2+Т1+Т3=1,3*103 Н*м 3.Определение диаметра вала из условия прочности
5.Принимаем, что φА=0
Дано: Т=2*103 Нмм а=1м d=100мм G=8*104МПа Требуется построить эпюры Тх и φх. Решение: 1.Статика ТА-Т1+ТС=0 –уравнение равновесия, одно уравнение с двумя неизвестными (система статически неопределима). 2.Геометрия φAB+ φBC=0 углы закручивания. 3.Физика
4.TAB=TA TBC=TA-T
3TA-2T=0
TAB= -TA=8*103 Нм ТBC=TA-T= -4*103 Нм 6.Определение углов закручивания φА=0
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.138 (0.01 с.) |

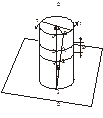 , при этом рассмотрим следующие допущения связанные с оценкой внутренних сил, напряжений и перемещений при кручении:
, при этом рассмотрим следующие допущения связанные с оценкой внутренних сил, напряжений и перемещений при кручении: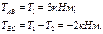
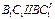
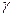 - относительный сдвиг;
- относительный сдвиг;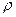 - текущий радиус (текущая полярная координата);
- текущий радиус (текущая полярная координата);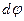 - элементарный угол закручивания на длине dx;
- элементарный угол закручивания на длине dx;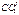 - линейное перемещение (относительный сдвиг);
- линейное перемещение (относительный сдвиг);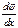 - относительный угол закручивания;
- относительный угол закручивания;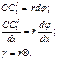
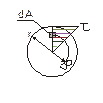
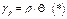
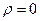 сдвиговой деформации нет, а при
сдвиговой деформации нет, а при 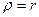 она максимальна.
она максимальна.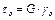 (1)
(1)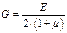 тогда из (*) и (1):
тогда из (*) и (1): 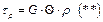
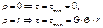
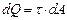 (3)
(3)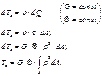
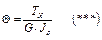
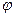 - полный угол закручивания; φ=Θ
- полный угол закручивания; φ=Θ 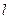
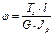 ≤[φ] –условие жесткости при кручении
≤[φ] –условие жесткости при кручении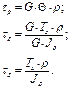
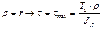
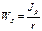
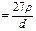 - полярный момент сопротивления (геометрическая характеристика сечения).
- полярный момент сопротивления (геометрическая характеристика сечения).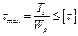
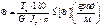
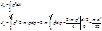
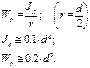
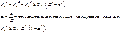
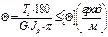 ,
, 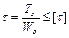
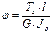
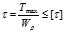
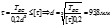
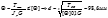 Анализируя результаты мы можем считать что более жестким является условие жесткости, тогда принимаем d=100мм
Анализируя результаты мы можем считать что более жестким является условие жесткости, тогда принимаем d=100мм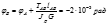
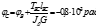
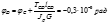 Пример решения статически неопределимой задачи.
Пример решения статически неопределимой задачи.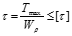
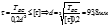 4. определение диаметра вала из условия жесткости
4. определение диаметра вала из условия жесткости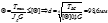 Анализируя результаты мы можем считать что более жестким является условие жесткости, тогда принимаем d=100мм
Анализируя результаты мы можем считать что более жестким является условие жесткости, тогда принимаем d=100мм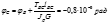
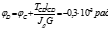 Пример решения статически неопределимой задачи.
Пример решения статически неопределимой задачи.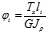
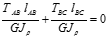 TA*a+(TA-T)2a=0
TA*a+(TA-T)2a=0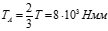
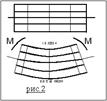 5.Определение крутящих моментов действующих в сечении вала.
5.Определение крутящих моментов действующих в сечении вала.