Кручение стержней с круглым поперечным сечением

 

ЦЕЛЬ РАБОТЫ

 

1. Ознакомиться с деформацией кручения.

2. Определить величины деформации и напряжений при кручении.

3. Определить модуль упругости материала скручиваемого стержня.

 

 

ОСНОВНЫЕ ПОЛОЖЕНИЯ

 

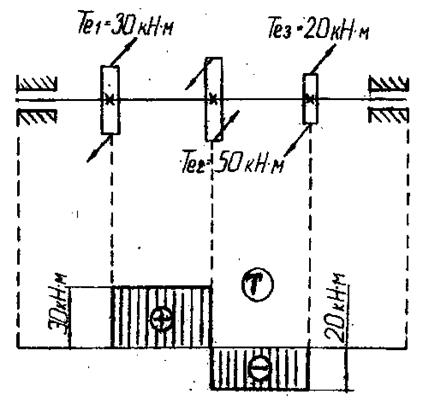
Деформацию кручения испытывают стержни при действии моментов внешних сил в плоскостях, перпендикулярных их продольной оси. С явлением кручения встречаются при расчетах валов, винтовых пружин и других элементов конструкций.

Моменты внутренних сил Т, возникающие в поперечных сечениях под действием внешних моментов Т_е и противодействующие внешним моментам, называют крутящими моментами. Крутящие моменты определяются с помощью метода сечений. На основании этого метода крутящий момент Т в сечении равен алгебраической сумме внешних скручивающих моментов Т_е, действующих по одну сторону от сечения. Для наглядности распределения Т по длине скручиваемого стержня и для нахождения опасного сечения с наибольшим крутя­щим моментом Т строят эпюры (графики распределения Т по длине стержня) этих моментов. На рис. 4.1 показана эпюра Т схемы нагружения тремя внешними моментами Т_е.

При построении эпюры Т проводят ось, параллельную оси стержня. Каждая ордината эпюры в принятом масштабе равна величине момента, действующего в том сечении, которому соответствует ордината. При расчетах на прочность и жесткость знак Т не играет большой роли; условимся считать крутящий момент положительным, если при взгляде в торец рассматриваемого сечения он направлен против хода часовой стрелки. Отметим, что в сечени­ях, где приложен внешний скручивающий момент Т_е, ордината эпюры Т меняется скачком на величину, равную значению момента Т_е.

Если на поверхности стержня круглого сечения нанести координатную сетку (рис. 4.2, а), то после деформации под действием внешнего скручивающего момента Т_е можно обнаружить следующее: прямоугольная сетка превратилась в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений τ в поперечных сечениях; поперечные сечения в процессе деформации остаются плоскими, расстояния между ними не изменяются, а первоначальные прямолинейные образующие превращаются в винтовые линии; радиусы поперечных сечений будут поворачиваться, оставаясь прямолинейными, т.е. поперечные сечения, оставаясь плоскими, поворачиваются друг относительно друга на некоторый угол. Эти наблюдения позволили составить представление о механизме деформации кручения. Постоянство длины и диаметра деформируемого стержня свидетельствует об отсутствии нормальных напряжений σ в поперечных и продольных сечениях. Там действуют только касательные напряжения τ. Эти напряжения распределены вдоль диаметра по линейному закону и имеют наибольшее значение на поверхности стержня (рис. 4.2, б).

Рис. 4.1

а б

 

 

Рис. 4.2

Касательное напряжение τ, МПа, на поверхности стержня круглого сечения радиуса r вычисляют по формуле

τ = Т∙r/I_p =T/W_p, (4.1)

где I_p, W_p – соответственно полярный момент инерции и полярный момент сопротивления поперечного сечения относительно центра, мм⁴, мм³.

Полярный момент инерции сечения учитывает величину площади сечения и его форму, для круга диаметром D

I_p ≈ 0,1∙D⁴. (4.2)

Полярный момент сопротивления W_p, мм³, вычисляют по формуле

 

W_p = I_p/r, ≈ 0,2D³, (4.3)

 

где r – радиус сечения, мм.

Угол закручивания φ поперечного сечения при постоянных по длине скручиваемого стержня величинах крутящего момента Т и жесткости G∙I_p вычисляют по формуле

φ = T∙ℓ/(G∙I_p), рад (4.4)

или

φ = T∙ℓ∙180º/(G∙I_p∙π), град, (4.5)

где G – модуль упругости материала стержня при сдвиге, МПа;

ℓ – длина стержня, мм.

 

Описание лабораторной установки

 

Установка (рис. 4.3) состоит из основания 1, скручиваемого стержня 2, направляющей 3, индикаторов 4, нажимных рычагов 5, навески гирь 6 и рычага 7. Кручение жестко закрепленного одним концом на основании 1 стержня 2 производят с помощью рычага 7 длиной h = 145 мм, на котором имеется подвеска 6 для набора гирь весом F =...Н. Углы поворота поперечных сечений измеряют индикаторами 4 с помощью нажимных рычагов 5 длиной R₁ и R₂. Один из индикаторов может перемещаться вдоль направляющей и устанавливаться совместно с относящимся к нему нажимным рычагом 5 в различных положениях ℓ₁, определяемых вариантом задания табл. 4.1. Положение второго индикатора неизменно ℓ₂ = 930 мм. К установке относится комплект быстросъемных стержней 2 круглого и кольцеобразного сечения из стали, латуни и алюминия.

Таблица 4.1

№ варианта (по № бригады)
ℓ1

 

Рис. 4.3

 

Порядок выполнения работы

 

1. Изучить описание лабораторной работы.

2. Используя пакет прикладных программ LAB2KRUT, сдать коллоквиум по лабораторной работе.

3. Получить у преподавателя вариант индивидуального задания

(табл. 4.1).

4. Индикатор и соответствующий нажимной рычаг установить в положение ℓ₁, определяемое вариантом задания по табл. 4.1.

5. Проверить "нуль" стрелочных индикаторов стрелочного часового ти­па при отсутствии грузов F на подвеске.

6. Установить на подвеску один из грузов. Определить ве­личину момента по формуле T=F∙h, где h – плечо силы тяжести в мм.

7. Определить экспериментальные значения деформаций φ₁, φ₂ с помощью индикаторов 4. Угол закручивания φ определить путем пересчета показаний индикаторов в радианы и вычислить по формуле

φ=K/R, (4.6)

где K – показания индикатора 4, мм;

R – длина плеча соответствующего прижимного рычага 5, мм (рис. 4.3).

8. Не известен материал стержня и, соответственно, не известно значение модуля упругости второго рода G. Модуль упругости определить по формуле

, (4.7)

9. Рассчитать по формулам (4.1) и (4.5) значения напряжения τ и углов φ₁, φ₂ в сечениях, где установлены индикаторы, т.е для участков ℓ₁, ℓ₂.

10. Меняя грузы (использовать не менее 5 сочетаний грузов), определить экспериментально и теоретически значения φ₁, φ₂ в зависимости от Т. Данные занести в табл. 4.2.

Для справки: Модуль упругости для стали G = 8∙10⁴ МПа, латуни

G = 3,8∙10⁴ МПа, алюминиевых сплавов G = 2,65∙10⁴ МПа.

Таблица 4.2

№ п/п	F, Н	T=F∙h, Нм	Теоретические значения	Экспериментальные значения	τ, МПа
φ1, рад	φ2, рад	К1	φ1, рад	К2	φ2, рад

 

Содержание отчета

 

1. Титульный лист.

2. Цель работы.

3. Краткие теоретические сведения.

4. Схема лабораторной установки.

5. Индивидуальное задание.

6. Таблица с результатами экспериментов (табл. 4.2).

7. Графики теоретической и экспериментальной зависимости угла поворота поперечного сечения стержня от величины крутящего момента.

8. Выводы по результатам исследований.

9. Литература.

 

 

Контрольные вопросы

 

1. Какую деформацию называют кручением?

2. Изменяется ли форма поперечных сечений при кручении?

3. Какие напряжения возникают в поперечных сечениях круглого стержня при кручении и как они распределяются по сечению?

4. Как определить величину напряжений при кручении?

5. Что такое полярный момент инерции сечения?

6. Что такое полярный момент сопротивления сечения?

7. От чего зависит величина угла закручивания стержня?

8. Что такое жесткость стержня при кручении?

9. Как в лабораторной работе определяется модуль упругости G второго рода материала стержня?

10. Каким образом в лабораторной работе измеряется угол поворота поперечного сечения стержня?

 

ЛИТЕРАТУРА

 

1. Красковский Е.Я., Дружинин П.А., Филатова Е.Н. Расчет и конструирование механизмов приборов и вычислительных систем: Учеб. пособие для приборостр. спец. вузов/ Под ред. Ю.А. Дружинина. 2-е изд. перераб. и доп. – М.: Высш. шк., 1991. – 480 с.

2. Ванторин В.Д. Механизмы приборных и вычислительных систем. – М.: Высш. шк., 1985, – 481 с.

3. Сурин В.М. Техническая механика: Учеб. пособие. – Мн.: БГУИР, 2004. – 292 с.