
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конструкции и параметры зубчатых механизмовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЛАБОРАТОРНАЯ РАБОТА № 1 ЛАБОРАТОРНАЯ РАБОТА № 2 ЛАБОРАТОРНАЯ РАБОТА № 3 ДОПУСКИ И ПОСАДКИ
ЦЕЛЬ РАБОТЫ
1. Изучение и практическое применение международной системы допусков и посадок. 2. Приобретение навыков работы с измерительными инструментами.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
В соединении двух деталей, входящих одна в другую, различают наружные (охватываемые) и внутренние (охватывающие) элементы деталей, называемые соответственно валом и отверстием. Размеры валов и отверстий могут быть как диаметральными, так и линейными. Основной размер отверстия и вала, определяемый из расчета на прочность или по конструктивным соображениям и служащий началом отсчета отклонений, называется номинальным размером (обозначается: d – для вала, D – для отверстия). Общий для вала и отверстия, составляющих соединение, размер называется номинальным размером соединения (d). Размер, полученный в результате непосредственного измерения изготовленной детали, называется действительным размером (dд, Dд). Максимальное и минимальное значения размера, между которыми должен находиться действительный размер годной детали, называют соответственно наибольшим(dmax, Dmax)и наименьшим (dmin, Dmin) предельными размерами(рис. 3.1).
Разность между наибольшим и наименьшим предельными размерами или алгебраическая разность между верхним и нижним отклонениями называют допуском размера (ТА – отверстия, ТВ – вала). Допуск характеризует точность изготовления детали: чем он меньше, тем выше точность.
Величину допуска в соответствии с системой допусков и посадок устанавливают в зависимости от номинального размера и условного уровня точности, называемого квалитетом (Qualitat). Квалитет – это совокупность допусков, соответствующих одинаковой степени точности.
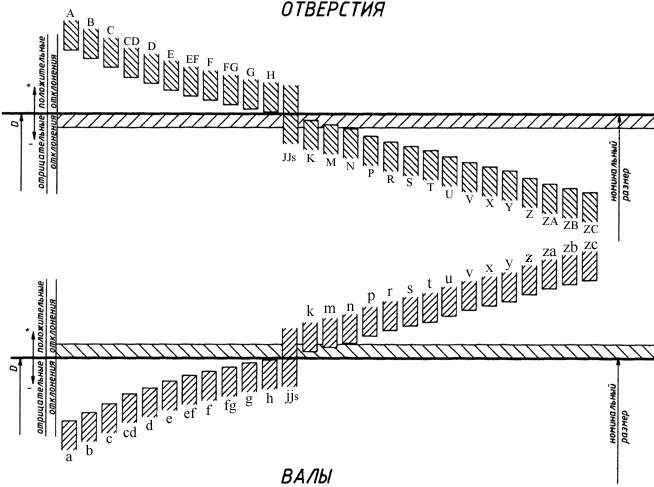
где Не предусмотрено строгое разграничение областей применения различных квалитетов, но практический опыт привел к следующему разграничению: – квалитеты 01; 0 и 1 предназначены для концевых мер длины; – квалитеты со 2 по 4-й – для средств измерений и особо точных изделий; – квалитеты с 5 по 13-й – для размеров различных соединений; – квалитеты с 12 по 17-й – для несопрягаемых (свободных) размеров. При графическом изображении поле допуска представляется в виде прямоугольника, расположенного по отношению к нулевой линии (номинальному размеру) так, что его верхняя сторона определяет верхнее отклонение, нижняя - нижнее. Величины этих отклонений (в микрометрах) проставляют около вершин правых углов прямоугольника. В зависимости от расположения поля допуска по отношению к номинальному размеру предусмотрено по 28 рядов (типов) отклонений для валов и отверстий. Каждый тип отклонения обозначается латинской буквой – малой, если отклонение относится к валу, и большой, если к отверстию (рис. 3.2).
Рис. 3.2 Можно сочетать любые типы отклонений с любыми квалитетами, что дает большое число различных по значению и положению полей допусков. Если величина допуска влияет на точность размера, то расположение поля допуска, т.е. выбор типа отклонения, влияет на величину действительного размера. Действительный размер при одинаковом допуске может быть всегда больше (отклонения для отверстий А, …, Н) или меньше номинального размера. На чертежах допуски на размеры проставляют после номинального размера одним из трех способов: условными обозначениями полей допусков, например 12е9; числовыми значениями предельных отклонений – При выборе квалитета точности исходят из технологических и экономических соображений. Назначение высоких квалитетов точности должно всегда серьезно обосновываться. Во всех случаях, когда это возможно, исходя из работоспособности и точности устройства необходимо стремиться к назначению невысокого по точности квалитета. Это имеет особое значение для отверстий, обработка которых сложнее, чем валов. Замена у отверстия поля допуска Н7 на Н9 уменьшает стоимость обработки деталей примерно на 20%. Размеры, характеризующие положение поверхностей, по которым отсутствует сопряжение, называют свободными. Отклонения свободных размеров на чертежах не проставляют. Но на поле чертежа делают запись: «Неуказанные предельные отклонения размеров: охватывающих по Н14; охватываемых по h14; остальных ±(1/2)IT14». Обозначения ±(1/2)IT рекомендуются для симметричных отклонений и отклонений элементов, которые не относятся к отверстиям и валам. При соединении двух деталей (вала и отверстия) в зависимости от взаимного расположения полей допусков можно получать различные виды соединений. Штангенинструменты К штангенинструментам относятся инструменты со штангой и линейным нониусом – это штангенциркули, штангенглубиномеры, штангенрейсмасы. Все они имеют две шкалы: основную, нанесенную на штанге, с интервалом деления 1 мм, и вспомогательную шкалу, нониус, по которой отсчитываются доли делений основной шкалы. Цена деления нониуса может быть 0,1; 0,05 и 0,02 мм. Рассмотрим нониус с ценой деления 0,1 мм. Вспомогательная шкала длиной 9 мм имеет 10 делений (рис. 3.6, а), т.е. расстояние между двумя соседними штрихами шкалы составляет 0,9 мм, что на 0,1 мм меньше расстояния между соседними штрихами основной шкалы, нанесенной на штанге. В том случае, когда нулевые деления шкалы штанги и нониуса совпадают, первый штрих нониуса отстает от первого штриха штанги на 0,1 мм, второй - на 0,2 мм, третий – на 0,3 мм, а последний десятый штрих нониуса будет совпадать с девятым штрихом шкалы штанги.
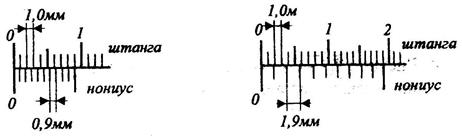
а б Рис. 3.6 Если измеряемый размер детали больше некоторого целого числа миллиметров, то нулевое деление нониуса не будет совпадать со штрихом шкалы штанги и дробная часть размера определяется по нониусу В соответствии с изложенным для определения размера с помощью штангенинструмента нужно отсчитать целое число миллиметров по шкале штанги до того места, где остановился нуль нониуса (если нуль не обозначен, то начальный штрих), затем найти, какое из делений нониуса совпадает с любым из штрихов основной шкалы. Номер совпавшего штриха укажет, сколько десятых частей миллиметра в данном размере. Для повышения удобства пользования используют штангенинструменты с вспомогательной шкалой, длина которой не 9, а 19 мм (растянутый нониус). В этом случае (см. рис. 3.6, б) интервал деления составит 19:10 = 1,9 мм, что дает также отставание в 0,1 мм от каждого второго деления основной шкалы. Принцип измерения остается тот же, но деления нониуса расположены реже, и отсчет производить удобнее. На рис. 3.7 представлен штангенциркуль ШЦ-1 с диапазоном измерений 0 – 150 мм и ценой деления 0,1 мм. Штангенциркуль состоит из штанги 1 и подвижной рамки 2. Штанга и подвижная рамка имеют губки 3 для измерения размеров наружных поверхностей и губки 4 для измерения размеров внутренних поверхностей (отверстий) деталей.
Рис. 3.7 Штангенциркуль имеет также глубиномер, состоящий из линейки 5, прикрепленной к подвижной рамке. Глубиномер выдвигается настолько, насколько смещается рамка, что дает возможность производить отсчет глубин непосредственно по шкале штанги и нониусу.
ЛАБОРАТОРНАЯ РАБОТА № 4 ЛАБОРАТОРНАЯ РАБОТА № 1 КОНСТРУКЦИИ И ПАРАМЕТРЫ ЗУБЧАТЫХ МЕХАНИЗМОВ ЦЕЛЬ РАБОТЫ
1. Ознакомиться с конструкциями зубчатых механизмов. 2. Получить навыки в составлении кинематических схем. 3. Определить передаточное отношение зубчатого механизма. 4. Определить геометрические параметры зубчатого колеса. 5. Дать графическую интерпретацию зубчатого колеса.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
Зубчатые механизмы наряду с другими видами механизмов предназначены для передачи движения от двигателя к исполнительному (рабочему) органу. Они выполняют следующие функции: понижают и повышают угловые скорости, соответственно повышая или понижая вращающие моменты; преобразовывают один вид движения в другой (вращательное движение в возвратно-поступательное или наоборот; равномерное в прерывистое); реверсируют движение, т.е. могут менять направление движение на противоположное. Простейший зубчатый механизм трехзвенный, в котором два подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательную пару. Зубчатое колесо с меньшим числом зубьев называется шестерней, с большим – колесом. Зубчатые механизмы классифицируют по следующим признакам: – по взаимному расположению геометрических осей валов – с параллельными осями (цилиндрические) (рис. 1.1, а, б), с пересекающимися осями (конические) (рис. 1.1, г), с перекрещивающимися в пространстве осями (червячные, винтовые); – по расположению зубьев относительно образующей обода колеса – прямозубые (рис. 1.1, а, г, I), косозубые (рис. 1.1, а, г, II), шевронные (рис. 1.1, а, III), с круговым зубом (рис. 1.1, г, III); – по взаимному расположению зубчатых колес – с внешним (рис. 1.1, а) и внутренним (рис. 1.1, б) зацеплением; в последнем в отличие от первого зубчатые колеса вращаются в одну сторону; – по числу пар колес, находящихся в зацеплении (ступеней), – одно-, двух- и многоступенчатые (рис. 1.1, е, ж, з); – по форме центроид колес – с круглыми и некруглыми (рис. 1.1, д) колесами; – по характеру относительного движения колес – с неподвижными геометрическими осями колес и планетарные (рис. 1.1, и, к, л), у которых имеются колеса (сателлиты) с подвижными осями вращения;
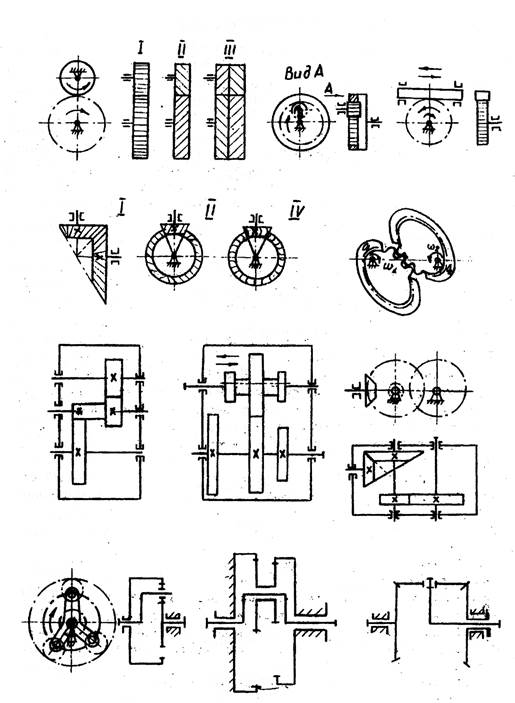
Рис. 1.1 – по величине окружной скорости – тихоходные (v < 3 м/с), среднескоростные (v = 3 … 15 м/с) и быстроходные (v > 15 м/с); – по степени защищенности – открытые, полузакрытые и закрытые; – по точности – 12 степеней (точность растет с уменьшением номера степени), обычно используют 7-ю, 8-ю и 9-ю степень точности, иногда в особо точных устройствах – 6-ю степень; – по форме профиля зубьев – с эвольвентным профилем, имеющим наибольшее применение, и другими – цевочным, часовым, зацеплением Новикова. Разновидностью зубчатой передачи является реечная передача (рис. 1.1, в), преобразующая вращательное движение шестерни в возвратно-поступательное движение рейки или наоборот. Зубчатые механизмы, используемые для понижения угловой скорости, называют редукторами, для повышения – мультипликаторами. Зубчатые механизмы – самый распространенный вид механизмов, используемых в приборо- и машиностроении благодаря ряду их достоинств: постоянство заданного передаточного отношения; отсутствие проскальзывания; способность передавать движение (энергию) между валами, как угодно расположенными в пространстве; высокий КПД (до 0,995); малые габариты и масса; применение в широком диапазоне передаточных отношений, скоростей и мощностей; надежность; простота обслуживания. К недостаткам зубчатых механизмов можно отнести: сложность изготовления колес и сборки передач из-за высоких требований к точности; шум, особенно при больших частотах вращения и невысокой точности; вибрации. Стандарт (ГОСТ 16530-83) регламентирует термины: передаточное число u = zк/zш – отношение числа зубьев колеса к числу зубьев шестерни; передаточное отношение i – отношение угловой скорости ведущего зубчатого колеса к угловой скорости ведомого. Передаточное число относится только к паре зубчатых колес. Оно всегда положительное, больше единицы, и является частным случаем передаточного отношения. Передаточное отношение может быть меньше единицы и отрицательным. Для редукторов |i| > 1, для мультипликаторов |i| < 1. Наиболее часто применяют механизмы с прямозубыми цилиндрическими колесами при параллельном расположении их осей. Постоянное передаточное отношение при зацеплении одной пары зубьев достигается при определенной форме профилей зубьев. Из всего многообразия сопряженных профилей зубьев наиболее распространены эвольвентные. Они отличаются относительной простотой изготовления зубьев, допускают изготовление одним инструментом колес с разным числом зубьев и возможность изменения в известных границах межосевого расстояния передачи без нарушения передаточного отношения. Рассмотрим элементы зубчатых колес (рис. 1.2), находящихся в зацеплении, в плоскости, перпендикулярной к оси вращения. По высоте снаружи зубья ограничены окружностью выступов диаметром d a, изнутри – окружностью впадин диаметром df. Боковые поверхности полного профиля зуба очерчены эвольвентами противоположных ветвей. Эвольвента представляет собой траекторию произвольной точки прямой, перекатывающейся без скольжения по окружности, называемой основной. Положительная ветвь эвольвенты получается при перекатывании производящей прямой против хода часовой стрелки, отрицательная – по ходу часовой стрелки. С увеличением радиуса основной окружности до бесконечности (зубчатая рейка) эвольвента превратится в прямую. Часть бокового профиля зуба очерчивается по переходной кривой, служащей плавным переходом от эвольвенты к окружности впадин. Наличие переходной кривой делает зуб более прочным у основания. При зацеплении одного колеса с другим появляется начальная окружность радиусом rw. Это окружность одного зубчатого колеса, перекатывающаяся без скольжения по окружности (поверхности) второго из зацепляющихся колес. Расстояние между одноименными профилями соседних зубьев по дуге окружности называется окружным шагом и обозначается pt. Значение этого параметра по начальным окружностям должно быть одинаковым у находящихся в зацеплении колес. Пользуясь шагом зацепления, можно выразить длину любой окружности колеса, умножив шаг на число зубьев z: ptz = πdt, (1.1) где t – индекс соответствующей окружности, например, p a, d a или pf, df.
Рис. 1.2 Величина pt выражается несоизмеримым числом, так как в правую часть условия (1.1) входит число π. Это затрудняет выбор размеров колес при их проектировании и изготовлении. Поэтому основным параметром принят не шаг, а отношение его к числу π. Эта величина называется модулем зацепления mt: mt = pt/π. [мм] (1.2) Шаг и модуль имеют индекс той окружности, по которой они измерены. Величины модулей для снижения номенклатуры и унификации режущего и контролирующего инструмента стандартизированы. Чаще всего, согласно стандартам, ограничиваются следующими значениями модуля (в миллиметрах): 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,20; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1,0; 1,25; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0. Окружность, по которой модуль имеет расчетное стандартное значение, называется делительной. Диаметр ее обозначается d, она является базовой для определения элементов зубьев и их размеров. Шаг и модуль по делительной окружности обозначают соответственно р и m. Диаметр делительной окружности d = mz. (1.3) Для наиболее распространенных неисправленных по высоте (нулевых) колес начальная и делительные окружности совпадают и передаточное отношение для пары таких колес будет равно i12 = ω1/ω2 = Часть зуба высотой h a, заключенную между окружностью выступов и делительной окружностью, называют головкой зуба, а часть зуба высотой hf, заключенную между делительной окружностью и окружностью впадин, – ножкой зуба. Основные геометрические параметры зубчатого колеса – диаметры выступов d a и впадин df, общая высота зуба h, высота головки h a и ножки hf, толщина зуба s и ширина впадин е между зубьями – выражаются через основной параметр зубчатой передачи – модуль m, по ГОСТ 9587-68. Высота головки зуба h a = h a *∙m, где h a * – коэффициент высоты головки, который в соответствии со стандартом равен единице (h a * = 1), а высота головки равна модулю (h a = m). Высота ножки зуба hf = (h a * + c*)m, где с = с*m – величина радиального зазора (см. рис. 1.2) между зубьями колес, находящихся в зацеплении; с* – коэффициент радиального зазора, который зависит от величины модуля: с* = 0,5 при m ≤ 0,5 мм, с* = 0,35 при 0,5 < m < 1 мм и с* = 0,25 при m ≥ 1 мм. Высота зуба h = h a + hf = m(2 + c*). Диаметры окружности выступов и впадин равны соответственно d a = d + 2h a = m(z + 2) и df = = d – 2hf = m(z – 2 – 2c*). Ширину зубчатого венца b принимают равной 2 … 6 модулям. Окружная толщина s зуба по делительной окружности s = p/2 = πm/2. Боковой зазор δ в зубчатом зацеплении устанавливается в зависимости от принятого вида сопряжения колес. Модуль и диаметр окружности выступов колеса связаны как
Наибольшее передаточное отношение (число) для простейшей зубчатой передачи рекомендуют принимать не более 8. В простой зубчатой передаче, состоящей из двух находящихся в зацеплении колес, при внешнем зацеплении колеса вращаются в разные стороны, поэтому передаточное отношение (1.4) отрицательное, а в передаче с внутренним зацеплением передаточное отношение положительное, т.е. i12 = ω1/ω2 = ±z2/z1, (1.6) где знак «–» принимают при внешнем зацеплении колес, знак «+» – при внутреннем. Передаточное отношение, которое можно воспроизвести одной парой зубчатых колес (исключая червячную передачу) невелико, так как минимальное и максимальное значения чисел зубьев колес ограничены и лимитируются определенными технологическими факторами. При необходимости получения больших передаточных отношений применяют сложные зубчатые механизмы, состоящие из нескольких простых цилиндрических, конических, червячных зубчатых механизмов, соединенных последовательно, т.е. применяют многоступенчатую передачу. Передача вращающего момента осуществляется последовательно с одного вала на другой через зубчатые колеса, причем на каждом промежуточном валу размещают по два колеса, одно из которых является ведомым по отношению к предыдущему, другое – ведущим по отношению к последующему. Передаточное отношение многоступенчатой передачи равно произведению передаточных отношений всех простых зубчатых передач, входящих в механизм, т.е. i1,n = i1,2·i2,3·…, (1.7) где i1,2, i2,3 – передаточное отношение соответственно первой, второй ступеней. Зависимость (1.7) можно выразить через числа зубьев колес: i1,n = (-1)k·(z2/z1)(z4/z3)…, (1.8) где z1, z2 – числа зубьев колес первой ступени передачи; z3, z4 – числа зубьев колес второй ступени передачи; k – число внешних зацеплений. Множитель (-1)k позволяет определить знак передаточного отношения сложного многоступенчатого механизма, т.е. направление вращения выходного звена по отношению к направлению вращения ведущего. Межосевое расстояние для пары зубчатых колес 1 и 2 определяется как a 12 = 0,5d1 + 0,5d1 = 0,5mz1 + 0,5mz2 = 0,5m(z1 + z2). (1.9) Чтобы провести полное кинематическое исследование механизма, надо знать его структуру(число звеньев, число и вид кинематических пар), размеры отдельных звеньев и их взаимное положение. Все эти данные мы получим, если составим кинематическую схему механизма, которая является его кинематической моделью. На кинематических схемах звенья обозначаются арабскими цифрами. При составлении схем применяются условные изображения кинематических пар и звеньев по ГОСТу (прил. 1).
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ, ОБОРУДОВАНИЕ
В работе необходимо провести кинематическое исследование зубчатого механизма. В состав механизма входят зубчатые колеса и валы зубчатых колес. Они установлены в подшипниках качения (скольжения), которые, в свою очередь, монтируются в корпусе редуктора. Для выполнения работы необходимы штангенциркуль, чертежный инструмент.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Составить кинематическую схему механизма, использовав условные обозначения (по ГОСТу) (прил. 1); пронумеровать все зубчатые колеса, начиная с ведущего, и указать в табл. 1.1 их числа зубьев. Таблица 1.1
2. Определить передаточные отношения зубчатых пар (ступеней). 3. Определить (по формуле 1.8) передаточное отношение механизма. 4. Полученное теоретическое значение передаточного отношения (iT) механизма сравнить с фактическим (iФ), которое можно определить путем проворачивания валов. Для этого рассчитывают количество оборотов ведущего вала соответствующее одному обороту ведомого. Части неполного оборота ведущего вала отсчитываются оценочно. 5. Измерить с помощью штангенциркуля диаметры выступов (da) зубчатых колес. 6. Используя формулу (1.5), определить модуль зацепления и округлить его до ближайшего стандартного значения. 7. Определить (по формуле 1.9) и сравнить с измеренным межосевое расстояние для одной пары колес. 8. Определить параметры (d, da, df, s, e, p) одного колеса (по указанию преподавателя). 9. Сделать чертеж выбранное колесо, для которого были определены размеры, на формате А4. Чертеж (эскиз) выполняется в карандаше чертежными инструментами или с помощью машинной графики (прил. 2).
Содержание отчета
1. Титульный лист. 2. Цель работы. 3. Классификация изученного механизма. 4. Кинематическая схема механизма – на листе формата А4. 5. Данные по числу зубьев, занесенные в табл. 1.1. 6. Определение передаточного отношения ступеней механизма и всего механизма в целом теоретическим и опытным путем (iT; iФ). 7. Чертеж (эскиз) колеса на листе формата А4. 8. Выводы. 9. Литература. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назначение, классификация зубчатых передач. 2. Передаточное отношение, передаточное число для многоступенчатой передачи. 3. Какое передаточное отношение считается положительным? 4. Как образуется эвольвентный профиль? 5. Достоинства эвольвентного зацепления. 6. Укажите типы плоских и пространственных зубчатых передач в зависимости от расположения осей вращения колес. 7. Понятие, размерность модуля зацепления. 8. Из каких частей состоит зуб?
ЛИТЕРАТУРА
1. Красковский Е.Я., Дружинин П.А., Филатова Е.Н. Расчет и конструирование механизмов приборов и вычислительных систем: Учеб. пособие для приборостр. спец. вузов/ Под ред. Ю.А. Дружинина. 2-е изд. перераб. и доп. – М.: Высш. шк., 1991. – 480 с. 2. Ванторин В.Д. Механизмы приборных и вычислительных систем. – М.: Высш. шк., 1985. – 416 с. 3. Сурин В.М. Техническая механика: Учеб. пособие. – Мн.: БГУИР, 2004. – 292 с. ЛАБОРАТОРНАЯ РАБОТА № 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.202.169 (0.015 с.) |

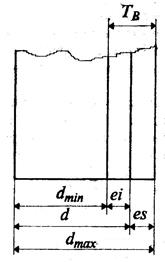 Алгебраическая разность между действительным и номинальным размерами называется отклонением. Алгебраическая разность между наибольшим и наименьшим предельными и номинальным размерами называется соответственно верхним (ЕS – отверстие, еs – вал) и нижним (ЕI – отверстие, еi – вал) отклонениями.
Алгебраическая разность между действительным и номинальным размерами называется отклонением. Алгебраическая разность между наибольшим и наименьшим предельными и номинальным размерами называется соответственно верхним (ЕS – отверстие, еs – вал) и нижним (ЕI – отверстие, еi – вал) отклонениями.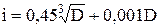 ,
,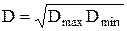 – среднегеометрический размер основного интервала диаметров, мм. Так, для 5-го квалитета а = 7, для 6-го, 7-го, 8-го и т.д. – соответственно 10, 16, 25 и т.д. Числа единиц допусков а, начиная с IT6, образуют геометрическую прогрессию со знаменателем ~ 1,6.
– среднегеометрический размер основного интервала диаметров, мм. Так, для 5-го квалитета а = 7, для 6-го, 7-го, 8-го и т.д. – соответственно 10, 16, 25 и т.д. Числа единиц допусков а, начиная с IT6, образуют геометрическую прогрессию со знаменателем ~ 1,6.
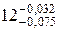 ; условными обозначениями полей допусков с указанием в скобках числовых значений предельных отклонений 12е9
; условными обозначениями полей допусков с указанием в скобках числовых значений предельных отклонений 12е9  .
.

 = d2/d1 = z2/z1. (1.4)
= d2/d1 = z2/z1. (1.4) m = da/(z+2). (1.5)
m = da/(z+2). (1.5)


