
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При получении точных перемещений применение дифференциальной винтовой передачи может быть предпочтительнее, чем уменьшение шага резьбы.Содержание книги
Поиск на нашем сайте
В винтовых механизмах используют цилиндрические резьбы с треугольным (метрическая), трапецеидальным и прямоугольным профилем. Метрическая резьба (см. рис. 2.4, а) имеет профиль равностороннего треугольника с углом профиля a = 60°. Вершины и впадины резьбы для уменьшения концентрации напряжений притуплены по прямой или по дуге. Радиальный зазор в резьбе делает ее негерметичной. Метрические резьбы делятся на резьбы с крупным (основным) и мелким шагом. Метрическая резьба обеспечивает лучшее направление винта или гайки в винтовых механизмах из-за малого радиального смещения по сравнению с трапецеидальной резьбой. В механизмах винт – гайка с шагами резьбы до 1 мм применяют только метрические резьбы из-за сложности изготовления с такими шагами ходовых резьб трапецеидального и прямоугольного профилей. Трапецеидальная резьба (см. рис. 2.4, б) – основная резьба в механизмах винт – гайка. Ее профиль – равнобокая трапеция с углом a = 30°. Резьба имеет меньшие по сравнению с резьбой треугольного профиля потери на трение, больший КПД, обеспечивает высокую точность осевого перемещения ведомого звена. Широко применяется для реверсивных передач винт – гайка. Прямоугольная резьба (см. рис. 2.4, в) с профилем в форме квадрата имеет самый высокий КПД, так как угол профиля резьбы a = 0. Резьба обладает пониженной прочностью. При износе образуются осевые зазоры, которые трудно устранить. Резьба применяется в малонагруженных передачах винт –гайка (перемещение головок записи и считывания информации в дисководах).
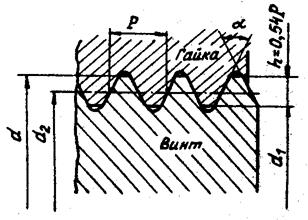
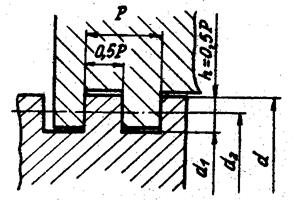 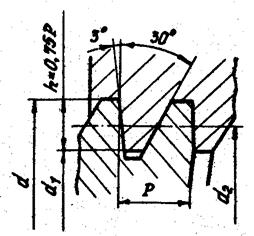
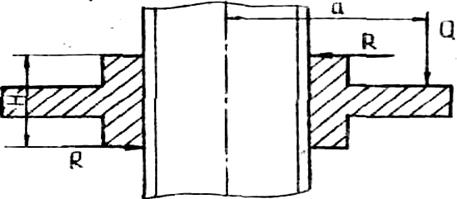
Рис. 2.4 Наибольшее применение в винтовых механизмах получили прямоугольные, трапецеидальные и метрические резьбы. Прямоугольную и трапецеидальную резьбы рекомендуют применять с шагом р > 1 мм, метрическую – в механизмах с мелкими шагами (р £ 1,0). КПД винтовых механизмов рассчитывают по формуле h = tgg / tg(g + rт), (2.2) где g – угол подъема винтовой линии; rт – приведенный угол трения. Для резьбы приведенный угол трения rт = arctg f¢ = arctg[f / cos(a/2)], (2.3) где f¢ – приведенный коэффициент трения скольжения; f – коэффициент трения скольжения между материалами винта и гайки; a – угол профиля резьбы. Для прямоугольной резьбы a = 0 и f¢ = f, для трапецеидальной резьбы a = 30° и f¢ = 1,04 f; для метрической резьбы a = 60° и f¢ = 1,15 f, т.е. при прочих равных условиях приведенный коэффициент трения у трапецеидальной резьбы на 4%, а у метрической резьбы на 15% больше, чем у прямоугольной. Но прямоугольная резьба менее прочна и износостойка, для нее трудна выборка радиальных и осевых зазоров, она в отличие от метрической и трапецеидальной не стандартизована. Формула (2.2) используется для вычисления КПД винтового механизма при действии осевой нагрузки на гайку. При эксцентричной нагрузке Q, действующей параллельно оси винта и приложенной к гайке на расстоянии а от оси (рис. 2.6), КПД вычисляют по формуле
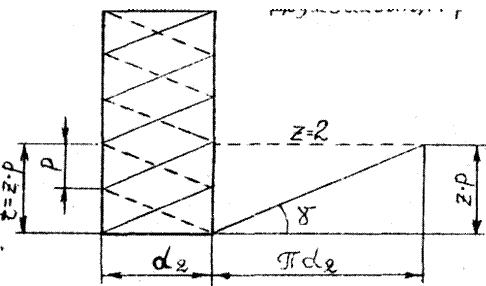
где Н – высота гайки (размеры а и Н в миллиметрах). КПД определяется прежде всего углом γ подъема винтовой линии. Учитывая зависимость (2.1), угол подъема связан с шагом p, числом z заходов и со средним диаметром d2 резьбы. При увеличении шага, числа заходов резьбы КПД механизма повышается. Средний диаметр d2 (в миллиметрах) для трапецеидальной резьбы (см. рис. 2.4, б) равен d2 = d – 0,5р, (2.5) где d – номинальный диаметр; р – шаг резьбы. Передача движения от гайки к винту возможна при γ > ρ, при ρ > γ передача движения от гайки к винту невозможна, механизм будет самотормозящимся.
Рис. 2.5
Рис. 2.6
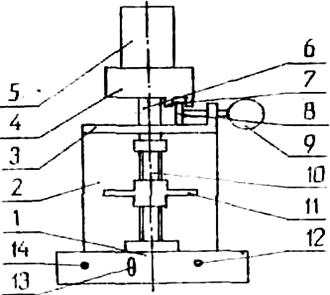
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Основные узлы установки (рис. 2.7) монтируются на основании 1. Электродвигатель 5 с редуктором 4 на подшипниках качения крепится в кронштейне 3. Приводной вал редуктора 6 соединен с винтом 10. При работе вращается винт, а гайка 11, связанная ползуном с пазом стойки, совершает поступательное движение вверх-вниз. Винт изготовлен из стали 45, а гайка – из бронзы БрОЦС5-5-5 с трапецеидальной резьбой Tr 14х2 (d = 14; p = 2; z = 1). Винт в нижней части опирается на шарикоподшипниковый подпятник. Движущий момент определяется путем измерения реактивного момента. Корпус двигателя и редуктор свободно вращаются в шарикоподшипниках кронштейна. При вращении винта статор двигателя увлекается в направлении вращения ротора. Рычаг 7, укрепленный на крышке редуктора, действует на плоскую пружину 8 и далее на индикатор 9. Индикатор 9, имея силовое замыкание с пружиной, показывает величину ее прогиба. По величине прогиба пружины определяют момент Тд, создаваемый двигателем, как Тд = k·μ, [Нмм], (2.6) где k – количество делений индикатора 9; μ – цена деления индикатора. Осевая нагрузка на гайку винтовой пары осуществляется грузами (4 шт. по 0,5 кг), которые устанавливают непосредственно на гайку 11. Эксцентричную нагрузку создают с помощью груза (с кольцом), подвешиваемого на одном из плеч гайки. Питание включают тумблером 13, при этом загорается сигнальная лампа 12. Рабочий цикл - ход гайки вверх, реверсирование двигателя, ход гайки вниз и выключение двигателя - происходит после нажатия кнопки 14. В результате тарировки измерительного устройства установлено, что цена деления индикатора 9, измеряющего крутящий момент на валу электродвигателя, μ = 3Нмм.
Рис. 3.7
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Установить силовое замыкание индикатора. 2. Проверить «нуль» индикатора. Изменение КПД от величины действующей на гайку осевой нагрузки проводят в следующей последовательности: 3. Теоретический КПД определяют по формуле (2.2). При этом: tg γ = p/(πd2), р = 2мм; d2 = 13 мм; угол трения ρ = arctg[f/cos(α/2)], где f = 0,1 – коэффициент трения скольжения для пары сталь-бронза; α = 30º – угол профиля трапецеидальной резьбы. 4. Действительный КПД при проведении экспериментов определяют по формуле ηд = Ту/Тд, (2.7) где Ту – необходимый для осуществления движения гайки уравновешивающий момент, действующий в перпендикулярной к оси винта плоскости, Тд – крутящий момент на валу двигателя, который определяется по формуле (2.6) путем измерения показаний индикатора. Необходимый для движения гайки момент Ту при нагружении осевой силой Q должен быть Ту = Q·tg(γ+ρ)·(d2/2). (2.8) 5. Установить на гайку один из грузов Q. Нажатием кнопки 14 (рис. 3.7) включить электродвигатель. За время движения гайки вверх-вниз снять 3 – 4 показания k индикатора 9 и занести среднее значение показаний в табл. 2.1. Измерения сделать отдельно для грузов 5; 10; 15 и 20 Н. В табл. 2.1 внести и результаты вычислений по формулам (2.6), (2.7) и (2.8). Таблица 2.1
Определение действительного КПД ηд при действии на гайку эксцентрично расположенной нагрузки проводят в следующей последовательности: 6. Подвесить груз Q = 10 Н с кольцом на гайку при величине плеча смещения груза относительно оси винта а = 50 мм. Нажатием кнопки 14 (рис. 2.7) включить электродвигатель. За время движения гайки вверх-вниз снять по 3 – 4 показания k индикатора и занести среднее значение показаний в табл. 2.2. Для выбранного значения а вычислить по формуле (2.4) величину теоретического КПД η механизма (f = 0,1; H = 26 мм). Величину действительного КПД ηд для выбранного значения плеча а определяют по формуле (2.7). Вращающий момент Тд электродвигателя рассчитывают по формуле (2.6). Необходимый для движения гайки вращающий момент Ту при эксцентрично расположенной нагрузке Q и приложенной к гайке на расстоянии а должен быть
где f – коэффициент трения скольжения в винтовой паре (f = 0,1); Н – высота гайки (Н = 26 мм); ρ – угол трения; γ – угол подъема винтовой линии; d2 – средний диаметр резьбы (d2 = 13 мм). Измерение проводят для 4 – 5 различных по величин значений a. Данные измерений и расчетов заносят в табл. 2.2
Таблица 2.2
СОДЕРЖАНИЕ ОТЧЕТА
1. Титульный лист. 2. Цель работы. 3. Кинематическая схема установки (с использованием прил. 1). 4. Формулы для определения теоретического КПД η, необходимого Ту и действительного Тд вращающего момента. 5. Таблицы результатов экспериментов (табл. 2.1 и 2.2). 6. Графики теоретического η и действительного ηд КПД при осевом нагружений гайки η = f(Q). 7. Графики теоретического η и действительного ηд КПД при эксцентричной нагрузке η = f(а). 8. Выводы. 9. Литература.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назначение винтовых механизмов. 2. Достоинства передач «винт – гайка». 3. Недостатки передач «винт – гайка». 4. Из каких материалов изготавливают звенья винтовых передач? 5. Достоинства дифференциальных винтовых передач. 6. Почему применяют трапецеидальную и прямоугольную резьбы с шагом более 1 мм в передачах «винт – гайка»? 7. Как изменяется КПД с увеличением числа заходов резьбы? 8. При каком условии винтовой механизм будет самотормозящимся? 9. Как и почему изменяется КПД с увеличением эксцентричной нагрузки на гайку?
ЛИТЕРАТУРА
1. Ванторин В.Д. Механизмы приборных и вычислительных систем. – М.: Высш. шк., 1985. – 416 c. 2. Вопилкин Е.А. Расчет и конструирование механизмов приборов и систем. – М.: Высш. шк., 1986. – 463 с. 3. Куркин В.И., Козинцов В.С. Детали механизмов радиоустройств. – М.: Высш. шк., 1988. – 256 с. 4. Сурин В.М. Техническая механика: Учеб. пособие. – Мн.: БГУИР, 2004. – 292 с.
ЛАБОРАТОРНАЯ РАБОТА № 3 ДОПУСКИ И ПОСАДКИ
ЦЕЛЬ РАБОТЫ
1. Изучение и практическое применение международной системы допусков и посадок. 2. Приобретение навыков работы с измерительными инструментами.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
В соединении двух деталей, входящих одна в другую, различают наружные (охватываемые) и внутренние (охватывающие) элементы деталей, называемые соответственно валом и отверстием. Размеры валов и отверстий могут быть как диаметральными, так и линейными. Основной размер отверстия и вала, определяемый из расчета на прочность или по конструктивным соображениям и служащий началом отсчета отклонений, называется номинальным размером (обозначается: d – для вала, D – для отверстия). Общий для вала и отверстия, составляющих соединение, размер называется номинальным размером соединения (d). Размер, полученный в результате непосредственного измерения изготовленной детали, называется действительным размером (dд, Dд). Максимальное и минимальное значения размера, между которыми должен находиться действительный размер годной детали, называют соответственно наибольшим(dmax, Dmax)и наименьшим (dmin, Dmin) предельными размерами(рис. 3.1).
Разность между наибольшим и наименьшим предельными размерами или алгебраическая разность между верхним и нижним отклонениями называют допуском размера (ТА – отверстия, ТВ – вала). Допуск характеризует точность изготовления детали: чем он меньше, тем выше точность.
Величину допуска в соответствии с системой допусков и посадок устанавливают в зависимости от номинального размера и условного уровня точности, называемого квалитетом (Qualitat). Квалитет – это совокупность допусков, соответствующих одинаковой степени точности.
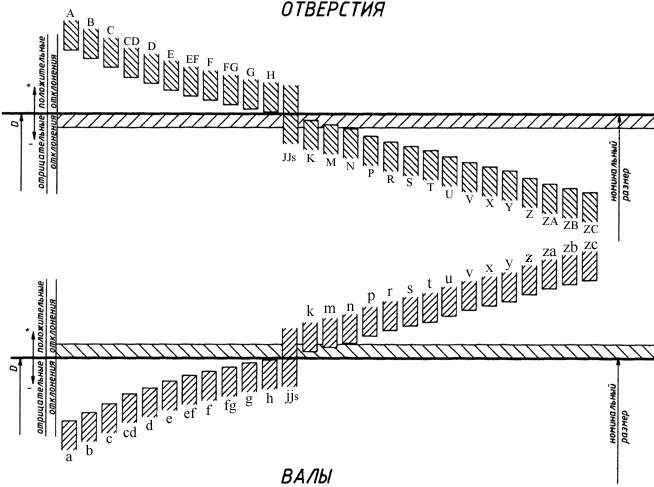
где Не предусмотрено строгое разграничение областей применения различных квалитетов, но практический опыт привел к следующему разграничению: – квалитеты 01; 0 и 1 предназначены для концевых мер длины; – квалитеты со 2 по 4-й – для средств измерений и особо точных изделий; – квалитеты с 5 по 13-й – для размеров различных соединений; – квалитеты с 12 по 17-й – для несопрягаемых (свободных) размеров. При графическом изображении поле допуска представляется в виде прямоугольника, расположенного по отношению к нулевой линии (номинальному размеру) так, что его верхняя сторона определяет верхнее отклонение, нижняя - нижнее. Величины этих отклонений (в микрометрах) проставляют около вершин правых углов прямоугольника. В зависимости от расположения поля допуска по отношению к номинальному размеру предусмотрено по 28 рядов (типов) отклонений для валов и отверстий. Каждый тип отклонения обозначается латинской буквой – малой, если отклонение относится к валу, и большой, если к отверстию (рис. 3.2).
Рис. 3.2 Можно сочетать любые типы отклонений с любыми квалитетами, что дает большое число различных по значению и положению полей допусков. Если величина допуска влияет на точность размера, то расположение поля допуска, т.е. выбор типа отклонения, влияет на величину действительного размера. Действительный размер при одинаковом допуске может быть всегда больше (отклонения для отверстий А, …, Н) или меньше номинального размера. На чертежах допуски на размеры проставляют после номинального размера одним из трех способов: условными обозначениями полей допусков, например 12е9; числовыми значениями предельных отклонений – При выборе квалитета точности исходят из технологических и экономических соображений. Назначение высоких квалитетов точности должно всегда серьезно обосновываться. Во всех случаях, когда это возможно, исходя из работоспособности и точности устройства необходимо стремиться к назначению невысокого по точности квалитета. Это имеет особое значение для отверстий, обработка которых сложнее, чем валов. Замена у отверстия поля допуска Н7 на Н9 уменьшает стоимость обработки деталей примерно на 20%. Размеры, характеризующие положение поверхностей, по которым отсутствует сопряжение, называют свободными. Отклонения свободных размеров на чертежах не проставляют. Но на поле чертежа делают запись: «Неуказанные предельные отклонения размеров: охватывающих по Н14; охватываемых по h14; остальных ±(1/2)IT14». Обозначения ±(1/2)IT рекомендуются для симметричных отклонений и отклонений элементов, которые не относятся к отверстиям и валам. При соединении двух деталей (вала и отверстия) в зависимости от взаимного расположения полей допусков можно получать различные виды соединений.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 971; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.47.194 (0.014 с.) |

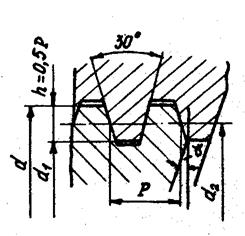 Упорная резьба (см. рис. 2.4, г) имеет профиль неравнобокой трапеции с углом a = 30°. Рабочая сторона профиля имеет угол наклона 3°, КПД этой резьбы выше, чем КПД трапецеидальной резьбы. Рекомендуется применять эту резьбу в механизмах винт – гайка при значительных односторонних осевых нагрузках.
Упорная резьба (см. рис. 2.4, г) имеет профиль неравнобокой трапеции с углом a = 30°. Рабочая сторона профиля имеет угол наклона 3°, КПД этой резьбы выше, чем КПД трапецеидальной резьбы. Рекомендуется применять эту резьбу в механизмах винт – гайка при значительных односторонних осевых нагрузках.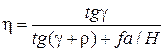 , (2.4)
, (2.4)

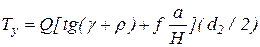 , (2.9)
, (2.9)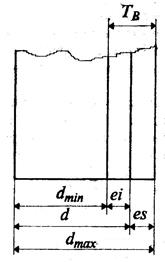 Алгебраическая разность между действительным и номинальным размерами называется отклонением. Алгебраическая разность между наибольшим и наименьшим предельными и номинальным размерами называется соответственно верхним (ЕS – отверстие, еs – вал) и нижним (ЕI – отверстие, еi – вал) отклонениями.
Алгебраическая разность между действительным и номинальным размерами называется отклонением. Алгебраическая разность между наибольшим и наименьшим предельными и номинальным размерами называется соответственно верхним (ЕS – отверстие, еs – вал) и нижним (ЕI – отверстие, еi – вал) отклонениями.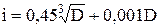 ,
,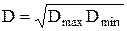 – среднегеометрический размер основного интервала диаметров, мм. Так, для 5-го квалитета а = 7, для 6-го, 7-го, 8-го и т.д. – соответственно 10, 16, 25 и т.д. Числа единиц допусков а, начиная с IT6, образуют геометрическую прогрессию со знаменателем ~ 1,6.
– среднегеометрический размер основного интервала диаметров, мм. Так, для 5-го квалитета а = 7, для 6-го, 7-го, 8-го и т.д. – соответственно 10, 16, 25 и т.д. Числа единиц допусков а, начиная с IT6, образуют геометрическую прогрессию со знаменателем ~ 1,6.
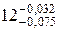 ; условными обозначениями полей допусков с указанием в скобках числовых значений предельных отклонений 12е9
; условными обозначениями полей допусков с указанием в скобках числовых значений предельных отклонений 12е9  .
.


