
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б15: Определение перемещений при изгибе.Содержание книги
Поиск на нашем сайте
Перемещения при изгибе. Понятия и определения.
Прогиб – это перемещение, перпендикулярное исходной оси балки в заданной точке А (у или f). Угол поворота сечения-α Имеет место перемещение двух типов: Линейные (прогиб), и угловые (перемещение перпендикулярно исходной оси балки в заданной точке) α-определяется положением касательной к точке А1. Искривленная при повороте ось балки называется упругой линией балки. Существует несколько методов определения перемещения при изгибе. Приближенное дифференциальное уравнение упругой линии
y’=α – угол наклона. у=f – прогиб.
После первого интегрирования получаем выражение для угла поворота сечения.
Интегрируя повторно, получаем выражение для определения прогиба.
Постоянные интегрирования находятся из граничных условий (в данном случае опирания балки).
Если Р посередине, то Пример: За ноль точку А не имеет смысла брать, ввиду того, что в этой точке появляется две реакции – поперечная сила и изгибающий момент. Если мы идем справа, и за начало принимаем точку В, то момент в сечении х определяется лишь действием распределенной нагрузки Q.
Тогда После интегрирования получаем:
Нужно получить постоянную интегрирования. Если Получаем Интегрируя второй раз по аналогии, определяем уравнение для отыскания прогиба, и сам прогиб в точке В.
при x=l y(0)
В итоге Универсальное уравнение упругой линии Для вывода универсального уравнения упругой линии воспользуемся приведенной схемой. Где: М – сосредоточенный момент; Р – сосредоточенная сила; q – распределенная нагрузка.
Интегрируя выражение 1 с учетом зависимости 2 получаем:
Интегрируя второй раз получаем:
При х=0, подставим это в 3 и 4
Для случая многократного повторения рассмотренных видов нагрузок, универсальные уравнения для определения прогиба и угла поворота в любой точке х принимают следующий вид: Уравнение для угла поворота в общем виде.
Уравнение для определения прогиба в общем виде.
Б16: Сложное сопротивление. Гипотезы прочности. Эквивалентные напряжения. Б17: Сложное сопротивление. Расчеты на прочность при совместном действии изгиба и кручения. Сложное сопротивление.
Теория прочности. Сложное сопротивление возникает тогда, когда в поперечном сечении бруса действуют несколько иловых факторов. Для сложного сопротивления выработаны теории, критерии (гипотезы) прочности, о преимущественном влиянии какого-либо из факторов. При этом, фактическое напряженное состояние заменяется эквивалентным линейным состоянием, которые приводятся к нормальным эквивалентным напряжениям. 1. Теория наибольших нормальных напряжений Принимается, что прочность зависит от величины наибольшего нормального напряжения.
Данная теория для пластичных материалов не подтверждается, но удовлетворительно работает при оценке прочности при растяжении для хрупких материалов. 2. Теория набольших линейных деформаций. Согласно этой теорией причиной разрушения является наибольшая одноосная (линейная деформация).
С использованием обобщенного закона Гука:
Данный критерий подтверждается для хрупких материалов. 3. Теория наибольших касательных напряжений
Этот критерий находит наибольшее применение для эквивалентных напряжений, выраженных формулой:
4. Энергетическая теория. Согласно этой теории, предельное состояние определяется предельным значением энергии растяжения, с учетом действия всех трех главных напряжений. Этот критерий находит наибольшее применение для эквивалентных напряжений, выраженных формулой.
Данная теория хорошо согласуется с расчетами пластичных материалов. 5.Теория Мора
k – коэффициент, учитывающий различное сопротивление материалов растяжению и сжатию. Изгиб с кручением В качестве примера на изгиб с кручением может быть рассмотрена работа вала для передачи любого вращательного движения. d – диаметр вала. Крутящий момент, передаваемый этим колесом:
Расчетная схема действия крутящих моментов:
рис.1 Изгибающий момент вызывает нормальное напряжение на этом валу.
Крутящие моменты вызывают касательные напряжения.
Используем третью теорию (теорию наибольших касательных напряжений) в виде:
При помощи вышеприведенного уравнения можно решать основные задачи сопротивления материалов применительно к изгибу с кручением.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.57.152 (0.007 с.) |



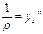
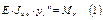






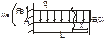

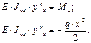

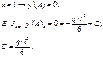
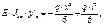


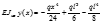











 в данном случае
в данном случае  - наибольшее главное напряжение.
- наибольшее главное напряжение. ≤[ε]
≤[ε] Умножив левую и правую часть на модуль упругости, получим:
Умножив левую и правую часть на модуль упругости, получим: В этом случае учитываются три главных напряжения.
В этом случае учитываются три главных напряжения.
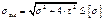

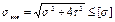 Данная теория удовлетворительна для пластичных материалов.
Данная теория удовлетворительна для пластичных материалов.
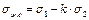 ≤[σ]
≤[σ]
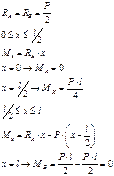




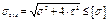


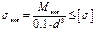 - условие прочности для изгиба с кручением.
- условие прочности для изгиба с кручением.


