
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статически неопределимые системыСодержание книги
Поиск на нашем сайте Если число неизвестных силовых факторов превышает число уравнений равновесия, то задача называется статически неопределимой. Разность между числом неизвестных и числом уравнений статического равновесия называется степенью статической неопределимости. Условие неразрывности деформаций. Мысленно рассеченные части деформированной конструкции должны в точности совпасть при совмещении в каждой точке по 6 компонентам перемещений (3 линейные и 3 вращательные). Это положение составляет условие неразрывности деформаций во всех сечениях и точках конструкции. Уравнения равновесия и условия связи деформаций (и перемещений) в совокупности дают достаточное число уравнений для однозначного описания и решения задачи. Нормальные и касательные напряжения Напряжение - это мера интенсивности распределения внутренних сил N по сечению F при dF,стремящемся к 0:
Вектор напряжений p может быть разложен на составляющие. Компонента напряжений, перпендикулярная к площадке сечения, называется нормальным напряжением и обозначается буквой s. Компонента напряжений действующая в плоскости площадки сечения, называется касательным напряжением и обозначается буквой t. Так, при растяжении протяженного образца с площадью поперечного сечения F силой N, нормальные напряжения s равны: s = N / F. (1.2) Если сечение площадью F нагружено перерезывающей поперечной силой Q, то в нем возникают касательные напряжения: t = kQ / F, (1.3) где k -коэффициент, зависящий от формы сечения, и имеющий значение, близкое к единице. Закон Гука Если до нагружения стержня его длина равна l, а после приложения силы равна l +D l, то относительное удлинение e определяется так: e =D l / l (1.4) В курсе сопротивления материалов рассматриваются задачи, для которых выполняется закон Гука: s = E e (1.5) Величина E представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода, который является физической константой материала и определяется экспериментально. Следовательно курс сопротивления материалов рассматривает преимущественно задачи для области нагружения, в которой материал ведет себя линейно. Подставив в закон Гука (1.5) выражения (1.2 и 1.4), получим формулу для вычисления удлинения образца: В технической литературе величины Е, s, t обычно задаются в размерности кгc/мм2, а в научной в Па (паскалях). 1 кгc/мм2 = 9,8*106 Па. В пособии используются обе системы. Деформации и перемещения Следует различать понятия деформации и перемещения. На рис.1.8 участок a деформируется, а участок b перемещается как единое целое, не испытывая деформаций.
Пример 1.1. (Расчет свободно подвешенного бруса)
Выясним, какова может быть максимально достижимая длина колонны буровых труб постоянного сечения, если она загружена только собственным весом. Трубы изготовлены из стали с удельным весом материала gт=7,9 г/см3. Колонна находится в утяжеленном глинистом растворе с удельным весом gр= 1,2. Введем понятие «приведенный» удельный вес материала gпр, который определяем с учетом закона Архимеда: γпр = γт – γр = 7,9 -1,2 = 6,7 г/см3 Определим общие выражения для напряжения и удлинения бруса, обозначив через l длину стержня, а через F - площадь поперечного сечения. Решение. Нормальная сила в сечении z равна весу нижележащей части стержня: N = γпр F z Максимальное значение нормальной силы N max реализуется в самом верхнем сечении колонны и равно весу бруса: N max = γпр F l Напряжение в произвольном сечении бруса составляет: s = N / F = γпр z. Максимальное значение напряжения равно: smax = Nmax / F = γпр l
Эпюры усилий, напряжений и деформаций показаны на рис.1.9. Перемещение D в сечении z, равное удлинению верхнего участка стержня, получаем путем интегрирования: Закон изменения D представляет собой квадратичную функцию, при этом наибольшее значение перемещения Dmax имеет место в нижнем торцевом сечении:
В рассматриваемом примере примем, что допускаемые напряжения [s]доп = 20000 кг/см2 (сталь 40ХНВ), а модуль упругости Е = 2.* 106 кг/см2. Максимально достижимая длина буровой колонны при заданных условиях равна: L = sдоп / g пр = 20000 / 6,7 = 2985м» 3 км Удлинение колонны под действием собственного веса: Δmax = g l2 / 2 E = 0,067* 6000002 / (2* 2* 106)» 5,0 м. Таким образом, при использовании бурильной трубы постоянного сечения, выполненной из конструкционной стали, проект по достижении глубины 15 км не мог быть осуществлен. Следующий шаг поиска следует выполнить для труб переменного сечения. Пример 1.2 При постановке задачи важно не только установить правильный закон распределения внешних сил, но и выявить природу их возникновения. Здесь можно выделить два крайних случая: когда заданы силы и когда заданы смещения.
|
|||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 (1.1)
(1.1) ( 1.6)
( 1.6)
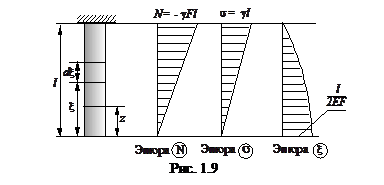 Рассмотрим расчетную схему, представленную на рис.1.3. Представим колонну бурильных труб в виде свободно подвешенного бруса постоянного сечения (рис.1.9).
Рассмотрим расчетную схему, представленную на рис.1.3. Представим колонну бурильных труб в виде свободно подвешенного бруса постоянного сечения (рис.1.9).
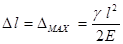

 Пусть на башне ферменной конструкции в четырех точках закреплено кольцо К (рис.1.10), на котором установлен резервуар с водой весом Р. Каждая из стоек фермы воспринимает соответствующую часть веса резервуара и может быть рассчитана на прочность и на устойчивость. Для них внешней нагрузкой является вес наполненного резервуара. Далее рассмотрим вопрос о прочности опорного кольца К.. Для решения подобных задач часто ошибочно формируется модель, изображенная на рис.1.11, где вес бака равномерно распределяется по кольцу и уравновешивается четырьмя реакциями опор. Такая схема нагружения не отражает реальность, поскольку кольцо, в отличие от фермы, не является свободно нагруженной системой. Кольцо прогнется ровно настолько, насколько прогнется несущий основную нагрузку донный шпангоут бака Ш. Последний же при изгибе в вертикальной плоскости обладает очень большой жесткостью, поскольку связан с цилиндрической стенкой бака. Нагружение и напряженное состояние кольца определяются не непосредственно весом бака, а теми прогибами, которые возникают в смежном несущем элементе. Если шпангоут бака удовлетворяет условиям прочности, то автоматически этим же условиям удовлетворяет и кольцо.
Пусть на башне ферменной конструкции в четырех точках закреплено кольцо К (рис.1.10), на котором установлен резервуар с водой весом Р. Каждая из стоек фермы воспринимает соответствующую часть веса резервуара и может быть рассчитана на прочность и на устойчивость. Для них внешней нагрузкой является вес наполненного резервуара. Далее рассмотрим вопрос о прочности опорного кольца К.. Для решения подобных задач часто ошибочно формируется модель, изображенная на рис.1.11, где вес бака равномерно распределяется по кольцу и уравновешивается четырьмя реакциями опор. Такая схема нагружения не отражает реальность, поскольку кольцо, в отличие от фермы, не является свободно нагруженной системой. Кольцо прогнется ровно настолько, насколько прогнется несущий основную нагрузку донный шпангоут бака Ш. Последний же при изгибе в вертикальной плоскости обладает очень большой жесткостью, поскольку связан с цилиндрической стенкой бака. Нагружение и напряженное состояние кольца определяются не непосредственно весом бака, а теми прогибами, которые возникают в смежном несущем элементе. Если шпангоут бака удовлетворяет условиям прочности, то автоматически этим же условиям удовлетворяет и кольцо.


