
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этап 1. Идеализация объекта.Содержание книги
Поиск на нашем сайте Р А З Д Е Л 1 СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ (Механика материалов) Г Л А В А 1 ОСНОВНЫЕ ПОЛОЖЕНИЯ Предмет курса Курс “Основы прочности” обобщает разделы механики конструкций, в первую очередь механику материалов, и строительную механику, в том числе МКЭ, а также дает обзор практики расчета и оптимизации конструкции, современного состояния, возможностей, перспектив и поисковых исследований. Традиционно термин «прочность» понимается как способность материала, из которого изготовлена конструкция, сопротивляться без разрушения воздействию внешних и внутренних сил. Отсюда возникло иное название механики материалов: «сопротивление материалов». Строгой математической наукой, поставляющей точные и доказанные решения в механике материалов является теория упругости. На основе этих решений и упрощающих приемов, достоверность которых подтверждена расчетными и экспериментальными исследованиями, сопротивление материалов дает простые в реализации методы, служащие основой для инженерного расчета конструкций. Методы решения типичных для машиностроения задач сосредоточены в курсах строительной механики (летательного аппарата, корабля и др.). Определение рациональных параметров для конструкций (формы, габаритов, сечений) производится на базе математических дисциплин, например, вариационного исчисления, реализованного в виде численных методов оптимизации и синтеза конструкций.
Объект исследования, используемые критерии, принципы и методы в этих дисциплинах в значительной мере являются пересекающимися множествами и в данном курсе рассматриваются в совокупности, как механика конструкции. Задачей механики конструкции является создание прочной конструкции, наилучшим образом соответствующей выбранным критериям. Основные задачи сопротивления материалов: - обеспечение прочности конструкции при заданном наборе внешних нагрузок; - определение и ограничение деформаций конструкции, то есть расчет на жесткость; - обеспечение устойчивости элементов конструкции; - определение частот и форм собственных колебаний конструкции. Инженерный расчет Расчет, выполненный с использованием методов и формул сопротивления материалов, часто называют инженерным расчетом. Погрешности расчета, вносимые принятыми в сопротивлении материалов допущениями, не превышают 3%. Инженерный расчет подразделяется на 3 этапа: Этап 1. Идеализация объекта. В реальной конструкции выделяют ее наиболее существенные особенности и отбрасывают малосущественные факторы. Конструкция сводится к расчетной схеме, состоящей из элементов, для которых определены законы поведения и взаимодействия (стержни, балки, мембраны, пластины, крупные сосредоточенные массы и др.). На рис.1.1 показан проект самолета «Сталкер-232» (Краматорск, Украина), а на рис.1.2 - его балочная расчетная модель. Показаны также основные сосредоточенные массы, которые учитываются при динамическом расчете.
Этап 2. Анализ расчетной схемы. Определяется напряженное и деформированное состояние (НДС) конструктивно-силовой схемы (КСС). Этап 3. Переход от схемы к конструкции. К полученным результатам следует подходить с учетом всех сделанных упрощений. Результаты, полученные для расчетной схемы, соотносятся с реальным объектом и делаются выводы о соответствии конструкции ее функциональному назначению. Реальный объект и расчетная схема Модель реальной конструкции или проекта, освобожденная от несущественных особенностей, носит название расчетной схемы. Пример 1.1.
Схематизация нагрузки. Для многих распространенных задач и видов нагружения известны готовые аналитические решения, или упрощенные методы расчета. Поэтому реальную нагрузку часто целесообразно представить в виде равномерно распределенной, либо заменить равнодействующей, или разложить на компоненты и так далее. Конструкция может рассчитываться на один или несколько случаев нагружения. Так, для самолета таковыми могут быть случаи взлета, посадки, маневра, болтанки, наддува, нагрева и др. Для антенн на космических орбитах важнейшим параметром является сохранение формы, то есть отсутствие деформаций. Соответственно различают расчеты по нагрузкам, по несущей способности, по деформациям и др. (см. пример 1.2). Принцип суперпозиции
d(q+P) = d(P+q) = d(P) + d (q) Для стержня, жестко заделанного по концам и равномерно нагретого, общая деформация есть сумма силовой и температурной деформации. Таким образом, для сложных задач можно получить общее решение как результат наложения частных решений. Принципу подчиняются системы, в которых соблюдается условие пропорциональности между перемещениями и внешними силами. Предполагается также обратимость нагрузки и разгрузки. Правомерно наряду с силовыми факторами рассматривать температурные и иные физические воздействия, учитывать зазоры. Принцип Сен-Венана.
Принцип Д’ Аламбера. Данный принцип гласит, что к движущейся с ускорением системе могут быть применены соотношения статики при условии, что в число внешних сил включена фиктивная сила инерции, равная произведению массы на ускорение, и направленная против ускорения. Принцип позволяет свести решение многих задач динамики к известным методам решений задач статики, что будет продемонстрировано в главе 11. Принцип доказывается аналитически. Классификация сил Внешние силы Внешние силы могут быть объемными, поверхностными, сосредоточенными. К объемным силам относят: гравитационные, инерционные, температурные, пьезоэлектрические, магнитострикционные, «памяти формы» и другие. В число внешних включаются и реакции связей, опор, дополняющих систему до равновесной. При расширении границ рассматриваемого объекта некоторые внешние силы становятся внутренними. Внутренние силы Внутренними силами называют силы внутри рассматриваемой области - между частями конструкции, между частицами вещества. Внутренние силы выявляются при мысленном рассечении конструкции. Такой прием носит название метода сечений. Внутренние силы всегда взаимны. Силовые факторы Сила, направленная вдоль оси протяженного элемента, вызывает либо его растяжение, либо сжатие. Поперечные силы вызывают срез поперечного сечения элемента. Сила, имеющая плечо относительно некоторой точки, создает момент силы, который в зависимости от направления может иметь характер крутящего, или изгибающего момента. Силы и моменты могут быть сосредоточенными и распределенными либо по линии, либо по поверхности. Сосредоточенные моменты, подобно сосредоточенным силам, могут быть изображены в виде вектора, и над ними могут выполняться аналогичные операции разложения. Базовые понятия Уравнения равновесия Для любой выделенной части конструкции или ее узла можно записать условия статического равновесия. Равенство нулю суммы проекций сил или моментов на координатные оси дает набор уравнений, необходимый для определения величины и знака этих сил и моментов. Если этих уравнений достаточно для решения задачи, то расчетная схема называется статически определимой. Закон Гука Если до нагружения стержня его длина равна l, а после приложения силы равна l +D l, то относительное удлинение e определяется так: e =D l / l (1.4) В курсе сопротивления материалов рассматриваются задачи, для которых выполняется закон Гука: s = E e (1.5) Величина E представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода, который является физической константой материала и определяется экспериментально. Следовательно курс сопротивления материалов рассматривает преимущественно задачи для области нагружения, в которой материал ведет себя линейно. Подставив в закон Гука (1.5) выражения (1.2 и 1.4), получим формулу для вычисления удлинения образца: В технической литературе величины Е, s, t обычно задаются в размерности кгc/мм2, а в научной в Па (паскалях). 1 кгc/мм2 = 9,8*106 Па. В пособии используются обе системы. Деформации и перемещения Следует различать понятия деформации и перемещения. На рис.1.8 участок a деформируется, а участок b перемещается как единое целое, не испытывая деформаций.
Пример 1.1. (Расчет свободно подвешенного бруса)
Выясним, какова может быть максимально достижимая длина колонны буровых труб постоянного сечения, если она загружена только собственным весом. Трубы изготовлены из стали с удельным весом материала gт=7,9 г/см3. Колонна находится в утяжеленном глинистом растворе с удельным весом gр= 1,2. Введем понятие «приведенный» удельный вес материала gпр, который определяем с учетом закона Архимеда: γпр = γт – γр = 7,9 -1,2 = 6,7 г/см3 Определим общие выражения для напряжения и удлинения бруса, обозначив через l длину стержня, а через F - площадь поперечного сечения. Решение. Нормальная сила в сечении z равна весу нижележащей части стержня: N = γпр F z Максимальное значение нормальной силы N max реализуется в самом верхнем сечении колонны и равно весу бруса: N max = γпр F l Напряжение в произвольном сечении бруса составляет: s = N / F = γпр z. Максимальное значение напряжения равно: smax = Nmax / F = γпр l
Эпюры усилий, напряжений и деформаций показаны на рис.1.9. Перемещение D в сечении z, равное удлинению верхнего участка стержня, получаем путем интегрирования: Закон изменения D представляет собой квадратичную функцию, при этом наибольшее значение перемещения Dmax имеет место в нижнем торцевом сечении:
В рассматриваемом примере примем, что допускаемые напряжения [s]доп = 20000 кг/см2 (сталь 40ХНВ), а модуль упругости Е = 2.* 106 кг/см2. Максимально достижимая длина буровой колонны при заданных условиях равна: L = sдоп / g пр = 20000 / 6,7 = 2985м» 3 км Удлинение колонны под действием собственного веса: Δmax = g l2 / 2 E = 0,067* 6000002 / (2* 2* 106)» 5,0 м. Таким образом, при использовании бурильной трубы постоянного сечения, выполненной из конструкционной стали, проект по достижении глубины 15 км не мог быть осуществлен. Следующий шаг поиска следует выполнить для труб переменного сечения. Пример 1.2 При постановке задачи важно не только установить правильный закон распределения внешних сил, но и выявить природу их возникновения. Здесь можно выделить два крайних случая: когда заданы силы и когда заданы смещения.
Р А З Д Е Л 1 СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ (Механика материалов) Г Л А В А 1 ОСНОВНЫЕ ПОЛОЖЕНИЯ Предмет курса Курс “Основы прочности” обобщает разделы механики конструкций, в первую очередь механику материалов, и строительную механику, в том числе МКЭ, а также дает обзор практики расчета и оптимизации конструкции, современного состояния, возможностей, перспектив и поисковых исследований. Традиционно термин «прочность» понимается как способность материала, из которого изготовлена конструкция, сопротивляться без разрушения воздействию внешних и внутренних сил. Отсюда возникло иное название механики материалов: «сопротивление материалов». Строгой математической наукой, поставляющей точные и доказанные решения в механике материалов является теория упругости. На основе этих решений и упрощающих приемов, достоверность которых подтверждена расчетными и экспериментальными исследованиями, сопротивление материалов дает простые в реализации методы, служащие основой для инженерного расчета конструкций. Методы решения типичных для машиностроения задач сосредоточены в курсах строительной механики (летательного аппарата, корабля и др.). Определение рациональных параметров для конструкций (формы, габаритов, сечений) производится на базе математических дисциплин, например, вариационного исчисления, реализованного в виде численных методов оптимизации и синтеза конструкций.
Объект исследования, используемые критерии, принципы и методы в этих дисциплинах в значительной мере являются пересекающимися множествами и в данном курсе рассматриваются в совокупности, как механика конструкции. Задачей механики конструкции является создание прочной конструкции, наилучшим образом соответствующей выбранным критериям. Основные задачи сопротивления материалов: - обеспечение прочности конструкции при заданном наборе внешних нагрузок; - определение и ограничение деформаций конструкции, то есть расчет на жесткость; - обеспечение устойчивости элементов конструкции; - определение частот и форм собственных колебаний конструкции. Инженерный расчет Расчет, выполненный с использованием методов и формул сопротивления материалов, часто называют инженерным расчетом. Погрешности расчета, вносимые принятыми в сопротивлении материалов допущениями, не превышают 3%. Инженерный расчет подразделяется на 3 этапа: Этап 1. Идеализация объекта. В реальной конструкции выделяют ее наиболее существенные особенности и отбрасывают малосущественные факторы. Конструкция сводится к расчетной схеме, состоящей из элементов, для которых определены законы поведения и взаимодействия (стержни, балки, мембраны, пластины, крупные сосредоточенные массы и др.). На рис.1.1 показан проект самолета «Сталкер-232» (Краматорск, Украина), а на рис.1.2 - его балочная расчетная модель. Показаны также основные сосредоточенные массы, которые учитываются при динамическом расчете.
|
|||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

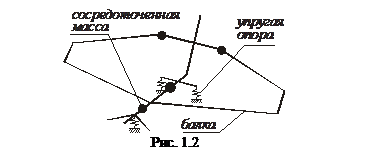
 Для конструкции самолета, вследствие ее симметрии, обычно бывает достаточно расчета одной части его модели, выделенной по соображениям симметрии. Конструкция вертолета, при нагружении ее несимметричными нагрузками (реактивная сила от несущего винта и боковая – от рулевого винта), чаще моделируется полной схемой. Вводится допущение, что материал элементов конструкции однороден и наделен заданными свойствами. Внешнее воздействие представляется набором сосредоточенных или распределенных сил и моментов сил. Этот этап в значительной мере опирается на опыт, интуицию, изобретательность расчетчика. Важно обеспечить приемлемую точность расчета при достаточно простой схеме.
Для конструкции самолета, вследствие ее симметрии, обычно бывает достаточно расчета одной части его модели, выделенной по соображениям симметрии. Конструкция вертолета, при нагружении ее несимметричными нагрузками (реактивная сила от несущего винта и боковая – от рулевого винта), чаще моделируется полной схемой. Вводится допущение, что материал элементов конструкции однороден и наделен заданными свойствами. Внешнее воздействие представляется набором сосредоточенных или распределенных сил и моментов сил. Этот этап в значительной мере опирается на опыт, интуицию, изобретательность расчетчика. Важно обеспечить приемлемую точность расчета при достаточно простой схеме. В 1960-е годы была поставлена задача пробурить мантию Земли, пройдя ее в наиболее тонком месте (около 15 км). При этом не было ясно, какие нагрузки, породы и температуры ждут конструкцию, а, соответственно, и какова должна быть структура колонны труб, каковы будут усилия от возможных «прихватов» колонны бурильных труб при вспучивании глинистых пластов породы и так далее. В этих условиях сам подход к формированию расчетной схемы имеет итерационный характер, и схема меняется не только в процессе проектирования, но и в ходе бурения. Столь длинная колонна буровых труб не может быть даже изображена в масштабе. В первом приближении может использоваться расчетная схема, показанная на рис.1.3. Кольская сверхглубокая скважина (Россия) стала крупнейшим «вертикальным» техническим сооружением мира. Она достигла отметки 12.262 метра от поверхности Земли. Именно при выборе расчетной схемы совершается наибольшее число ошибок. Основная масса консультаций по инженерным расчетам связана с обсуждением и формированием расчетных схем и выяснением вопросов их нагружения.
В 1960-е годы была поставлена задача пробурить мантию Земли, пройдя ее в наиболее тонком месте (около 15 км). При этом не было ясно, какие нагрузки, породы и температуры ждут конструкцию, а, соответственно, и какова должна быть структура колонны труб, каковы будут усилия от возможных «прихватов» колонны бурильных труб при вспучивании глинистых пластов породы и так далее. В этих условиях сам подход к формированию расчетной схемы имеет итерационный характер, и схема меняется не только в процессе проектирования, но и в ходе бурения. Столь длинная колонна буровых труб не может быть даже изображена в масштабе. В первом приближении может использоваться расчетная схема, показанная на рис.1.3. Кольская сверхглубокая скважина (Россия) стала крупнейшим «вертикальным» техническим сооружением мира. Она достигла отметки 12.262 метра от поверхности Земли. Именно при выборе расчетной схемы совершается наибольшее число ошибок. Основная масса консультаций по инженерным расчетам связана с обсуждением и формированием расчетных схем и выяснением вопросов их нагружения. Нагружение и деформации (d) не зависят от порядка приложения сил, и действие суммы сил равняется сумме их действий (рис1.6). Пусть к телу приложены сосредоточенная нагрузка Р и распределенная нагрузка q, тогда принцип можно записать в виде:
Нагружение и деформации (d) не зависят от порядка приложения сил, и действие суммы сил равняется сумме их действий (рис1.6). Пусть к телу приложены сосредоточенная нагрузка Р и распределенная нагрузка q, тогда принцип можно записать в виде: На расстояниях, превышающих характерные области приложения нагрузки (b на рис 1.7), напряжения и деформации для всех статически эквивалентных сил практически одинаковы. Иначе говоря, по мере удаления от точки приложения нагрузки особенности способа ее приложения сглаживаются и происходит выравнивание силовых потоков. Как и многие другие принципы, принцип Сен-Венана в общем виде не доказывается, но в частных случаях полностью подтверждается методами теории упругости и экспериментами.
На расстояниях, превышающих характерные области приложения нагрузки (b на рис 1.7), напряжения и деформации для всех статически эквивалентных сил практически одинаковы. Иначе говоря, по мере удаления от точки приложения нагрузки особенности способа ее приложения сглаживаются и происходит выравнивание силовых потоков. Как и многие другие принципы, принцип Сен-Венана в общем виде не доказывается, но в частных случаях полностью подтверждается методами теории упругости и экспериментами. ( 1.6)
( 1.6)
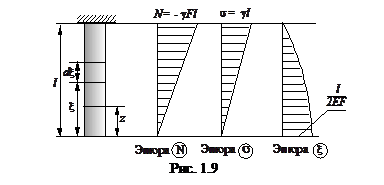 Рассмотрим расчетную схему, представленную на рис.1.3. Представим колонну бурильных труб в виде свободно подвешенного бруса постоянного сечения (рис.1.9).
Рассмотрим расчетную схему, представленную на рис.1.3. Представим колонну бурильных труб в виде свободно подвешенного бруса постоянного сечения (рис.1.9).
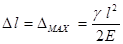

 Пусть на башне ферменной конструкции в четырех точках закреплено кольцо К (рис.1.10), на котором установлен резервуар с водой весом Р. Каждая из стоек фермы воспринимает соответствующую часть веса резервуара и может быть рассчитана на прочность и на устойчивость. Для них внешней нагрузкой является вес наполненного резервуара. Далее рассмотрим вопрос о прочности опорного кольца К.. Для решения подобных задач часто ошибочно формируется модель, изображенная на рис.1.11, где вес бака равномерно распределяется по кольцу и уравновешивается четырьмя реакциями опор. Такая схема нагружения не отражает реальность, поскольку кольцо, в отличие от фермы, не является свободно нагруженной системой. Кольцо прогнется ровно настолько, насколько прогнется несущий основную нагрузку донный шпангоут бака Ш. Последний же при изгибе в вертикальной плоскости обладает очень большой жесткостью, поскольку связан с цилиндрической стенкой бака. Нагружение и напряженное состояние кольца определяются не непосредственно весом бака, а теми прогибами, которые возникают в смежном несущем элементе. Если шпангоут бака удовлетворяет условиям прочности, то автоматически этим же условиям удовлетворяет и кольцо.
Пусть на башне ферменной конструкции в четырех точках закреплено кольцо К (рис.1.10), на котором установлен резервуар с водой весом Р. Каждая из стоек фермы воспринимает соответствующую часть веса резервуара и может быть рассчитана на прочность и на устойчивость. Для них внешней нагрузкой является вес наполненного резервуара. Далее рассмотрим вопрос о прочности опорного кольца К.. Для решения подобных задач часто ошибочно формируется модель, изображенная на рис.1.11, где вес бака равномерно распределяется по кольцу и уравновешивается четырьмя реакциями опор. Такая схема нагружения не отражает реальность, поскольку кольцо, в отличие от фермы, не является свободно нагруженной системой. Кольцо прогнется ровно настолько, насколько прогнется несущий основную нагрузку донный шпангоут бака Ш. Последний же при изгибе в вертикальной плоскости обладает очень большой жесткостью, поскольку связан с цилиндрической стенкой бака. Нагружение и напряженное состояние кольца определяются не непосредственно весом бака, а теми прогибами, которые возникают в смежном несущем элементе. Если шпангоут бака удовлетворяет условиям прочности, то автоматически этим же условиям удовлетворяет и кольцо.


