
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение внутренних усилий в заданной статически неопределимой системеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Способы определения М, Q, N: 1.найденные из канонических уравнений усилия Х1, Х2,.., Хn прикладываются как дополнительная внешняя нагрузка к статически определимой основной системе. Далее эта система рассчитывается с помощью уравнений равновесия. Этот способ применяется в основном для простейших рам и балок(степень стат неопределимости <2).
2.Основная система, эквивалентная заданной уже рассчитывалась на отдельные частные воздействия:
Mp, Qp, Np – внутренние усилия в основной системе от внешней нагрузки. Значения M, Q, N вычисленные по данным формулам часто называют окончательными усилиями основной системы. Особенности вычисления Q и Nв балках и рамах, работающих на изгиб: В этих конструкциях перемещения Для них строим эпюру Qпо эпюре М, а Nпо Q. Если эпюра М прямолинейна, то удобнее на основании дифференциальной зависимости Q=dM/dz находить Qкак тангенс угла наклона эпюры М.
Если эпюра моментов не прямолинейна, то удобно вырезать участок, приложить к нему нагрузку, а в местах сечений неизвестные Qи известные Mвзять из эпюр и составить уравнение равновесия. Значение Nнаходится из условия равновесия отдельных узлов или частей конструкции.
Мы делали в расчётке: 1. Определить степень статической неопределимости и основную систему 2. Составить систему канонических уравнений 3. Построение единичных и грузовой эпюр 4. Вычисление единичных и грузовых премещений (с проверкой правильности) 5. Решение системы канонических уравнений 6. Построение эпюры M(сумма произведений единичных эпюр на единичные перемещения) 7. Статическая и деформационная проверка эпюры М 8. Построение эпюры Q 9. Построение эпюры N
48 кульман тоже самое что и 47 скинуто
49. Расчет статически неопределимых систем на температурное воздействие В плоской п раз кинематически неопределимой стержневой системе краевые волокна всех или части элементов испытывают воздействие температурного поля (рис. 20.4,а). Характеристиками этого поля для k-го стержня сооружения являются: перепад приращения температуры по высоте поперечного сечения приращение температуры на уровне его центра тяжести. Наложением п угловых и линейных связей образуем основную систему метода перемещений заданного сооружения (рис. 20.4,6). Неизвестные угловые и линейные перемещения его узлов Z1, Z2,..., Z;,..., Zj,..., Zn определим из условий равенства нулю реакций в наложенных связях от их смещения на величины Z1… Z2.. Z... Zj..... Zn и от заданного изменения температуры. Используя принцип независимости действия сил и повторяя выкладки,получим систему канонических уравнений метода перемещений для определения неизвестных Zb Z2,..., Z,..... Zj,..., Zn в случае температурного воздействия на сооружение r11 Z1+r12 Z2+• • •+r1i Z1+• • •+rij Zj+• • •+r1n Zn+Ri t = 0, r1iZi+r12Z2+---+r11Zi+---+r1jZj+---+rmZn+R1t = 0, f (20.2) rni Zi+r„2 Z2+• • •+rn; Z+• • •+rnj Zj+• • •+ rnn Z„+Rnt - °- Величины главных rn и побочных ru коэффициентов системы уравнений (20.2) не зависят от вида воздействия на сооружение и определяются по-прежнему. Свободные члены системы канонических уравнений (20.2) Rit - это реакции в i-x наложенных связях от изменения температуры в основной системе метода перемещений. Они определяются по эпюрам внутренних усилий (в рамках и балках - по эпюрам изгибающих моментов), построенным в основной системе от температурного воздействия статическим способом, т.е. из условий равновесия узлов и отдельных частей сооружения. Эпюра изгибающих моментов Mt от изменения температуры в основной системе метода перемещений складывается из двух эпюр: M't - от неравномерных приращений температуры и эпюры М't - от равномерных. Для построения эпюры изгибающих моментов M't от неравномерных приращений температуры Дельта t0nr,k используются стандартные задачи. Равномерное приращение температуры Дельта t0o,k в основной системе метода перемещений вызывает линейные смещения узлов сооружения и, следовательно, перекосы его элементов, численные значения которых можно получить, используя план перемещений. В данном случае при построении этого плана необходимо учитывать продольные перемещения стержней, вызванные их равномерным нагреванием или охлаждением. Зная перекосы стержней, эпюру изгибающих моментов М"t в основной системе метода перемещений построим с помощью стандартных задач, полученных от линейных кинематических воздействий. Окончательную эпюру изгибающих моментов Mt в заданном сооружении от температурного воздействия после решения системы уравнений (20.2) получим, используя соотношение: Mt = M1Z1+M2Z2+…+MiZi + …+MjZj+…+MnZn+M1(20.3)В формуле (20.3) Mt = M't + Mt".Эпюры поперечных и продольных сил Qt и Nt построим по эпюре изгибающих моментов Mt, используя условия равновесия отдельных элементов и узлов заданного сооружения. Эпюры внутренних усилий Mt, Qt и Nt, полученные методом перемещений, построены правильно, если выполнена статическая проверка решения задачи, т.е. если все узлы и любые части заданного сооружения находятся в равновесии.
50. Расчёт стержневых статически неопределимых систем на кинематическое воздействие В плоской стержневой системе, степень статической неопределимости которой равна n, имеет место n независимых друг от друга кинематических возмущений, например, смещений линейных и угловых опорных связей (рис. 7.30,а). Жесткостные характеристики поперечных сечений элементов системы любого k-го участка на изгиб EJk, сдвиг GAk и растяжение–сжатие EAk примем постоянными.
Удаляя из заданного сооружения n лишних связей (рис. 7.30,б), образуем статически определимую основную систему метода сил (ОСМС). Особое внимание при выборе основной системы следует обращать на удаление связей, получивших в рассчитываемом сооружении перемещение. В частности, при наличии кинематического возмущения линейной связи её отбрасывание недопустимо, так как в этом случае из расчётной схемы основной системы исключается связь с диском "земля", являющимся причиной рассматриваемого линейного смещения по направлению опорной связи. В этом случае в произвольное сечение смещаемой опорной связи вводится поступательный шарнир (рис. 7.30,б – правая вертикальная опора).
Неизвестные метода сил X1, X2, …, Xj, …, Xn определим из условий равенства нулю перемещений по направлениям Xi (i = 1, 2, …, n) в основной системе метода сил от неизвестных этого метода и заданного смещения связей. Повторяя выкладки, приведённые в п. 7.1.2, получим систему канонических уравнений для определения неизвестных метода сил в случае кинематического воздействия на сооружение. Строка i этой системы уравнений имеет вид:
. Главные и побочные коэффициенты системы канонических уравнений определяются по формулам (7.5)–(7.6) в общем случае плоских стержневых систем и формулам (7.8)–(7.9) для рам и балок (см. п. 7.1.2). Свободный член j-й строки системы канонических уравнений есть перемещение по направлению усилия Xi в i-й удалённой лишней связи в основной системе метода сил от заданного кинематического возмущения. В статически определимой основной системе, принятой для расчёта, указанное перемещение определяется по формуле:
.
В формуле (7.44) – реакция в k-й связи, получившей кинематическое воздействие, от Xi = 1 в статически определимой основной системе; – величина кинематического воздействия, например, смещения k-й опорной связи.
Как и при температурном воздействии, значения жесткостных характеристик поперечных сечений элементов сооружения EJk, GAk, EAk не входят в соотношение (7.44). Это значит, что численные значения усилий в лишних связях и, следовательно, внутренних усилий в заданном сооружении, есть функции абсолютных значений жесткостей поперечных сечений стержней.
Вычислив из системы канонических уравнений усилия в лишних связях, мы расчёт статически неопределимого сооружения на кинематическое воздействие (рис. 7.30,а) свели к расчёту статически определимой основной системы метода сил (рис. 7.30,б). Так как кинематическое воздействие в статически определимых сооружениях внутренних усилий не вызывает, то величины изгибающих моментов Мс, поперечных Qc и продольных сил Nc в сечениях заданного сооружения в этом случае определяются только усилиями в лишних связях X1, X2, …, Xj, …, Xn. Имея эпюры внутренних усилий Mj, Qj, Nj от Хj = 1 в основной системе и применяя принцип независимости действия сил, получим:
Mс = M1X1 + M2X2 + … + MjXj + … + MnXn,
Qс = Q1X1 + Q2X2 + … + QjXj + … + QnXn, (7.45)
Nс = N1X1 + N2X2 + … + NjXj + … + NnXn.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 857; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.008 с.) |



 +
+  =0; x1=-
=0; x1=- 



 поэтому достаточно собрать результаты отдельных частных расчетов.
поэтому достаточно собрать результаты отдельных частных расчетов.

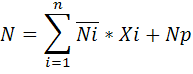
 – внутренние усилия в основной системе от Хi=1.
– внутренние усилия в основной системе от Хi=1. и
и  определялись с учетом только моментов, т.е.
определялись с учетом только моментов, т.е.  и Qp, Np в процессе расчета не определялись.
и Qp, Np в процессе расчета не определялись.
 Рис.7.30
Рис.7.30 (7.43)
(7.43) (7.44)
(7.44)


