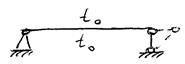Мгновенно изменяемые системы. Центр вращения. Фиктивный шарнир.

Мгновенно изменяемая система - это такая система, которая занимает промежуточное положение между геометр. измен. и геометр. неизмен. системами. Она допускает бесконечно малые перемещения без деформаций (ст1), затем её связи занимают новое положение и дальнейшее перемещение сопровождается деформацией (ст2).

Во второй стадии система работает как геом. неизмен, но возникающие в её элементах усилия достигают недопустимо больших значений, поэтому на практике таких систем необходимо избегать.

Данный термин никак не связан со временем, т.к. рассматривает задачи статики.

Для всякой изменяемой системы существует центр вращения -точка, относительно которой конструкция поворачивается под дей­ствием нагрузки.

Возможен случай, когда после поворота системы ее диски и опорные стержни занимают новое положение, и система становит­ся геометрически неизменяемой. Тогда точка, относительно кото­рой происходит поворот системы в первый момент нагружения, является мгновенным центром вращения.

Два стержня в плоской системе эквивалентны шарниру, нахо­дящемуся в точке их пересечения. Точку пересечения осевых ли­ний двух стержней называют фиктивным шарниром.

 

 

7

 

 

 

Число степеней свободы и степень изменяемости плоской стержневой системы

 

Кинематический анализ сооружений: аналитические методы. Необходимое аналитическое условие геометрической неизменяемости.

 

Существуют такие системы, в которых соединение элементов нельзя проанализировать по принципам соед. 2-х или 3-х дисков.

для таких систем правильность расположения связи определяется следующим способом:

1. система уравнений равновесия

S₁…S_n – внутренние усилия элементов систем и опорных связей (N, Q, M, V …)

a_ij (i, j = 1…n) – коэффициент, кот. опред. через геометрические параметры конструкции.

F₁…F_n – соот. внеш. нагрузки.

2. Опред. значение определителя системы

3. Если , то система геометрически изменяемая, если , то не изменяемая.

Другим аналитическим методом кинематического анализа явл. метод нулевой нагрузки:

при отсутствии нагрузки определяем усилие элементов системы, если они нулевые, то система неизменяемая, если же они оказываются не определимы – система изменяемая.

 

Необходимое аналитическое условие геометрической неизменяемости W .

Возможны 3 случая:

1) W>0 система содержит недостаточное для геометрической неизменяемости количества связей, она является механизмом

2)W=0 система имеет минимально необходимое кол-во связей и при правильной их расстановке геометрически неизменяема и статически определима.

3)W<0 система содержит избыточное кол-во связей при правильной расстановке которых она геометрически неизменяема и статически неопределима.

 

Основные свойства статически определимых систем

Необходимым и достаточным условием статической определимости системы является её мгновенная и геометрическая неизменяемость и отсутствие лишних связей. Заметим, что при расчетах по деформ. схеме все системы явл. Статически неопределимы. Внутрение усилия при выполнении всех гипотез определяются по недеформированной схеме, поэтому конструкция для которой W=0 статически-определима.

Св-ва:

1) Все связи статически определимых систем являются абсолютно неопределимыми. При удалении любой из них W>0 и конструкция становится изменяемой.

2) Каждой конкретной нагрузке соответствует определимые конечные внутренние усилия(св-во ед. решения). При отсутвии нагрузки усилии =0.

3) Самая уравновешенная нагрузка приложенная к локальной части конструкции вызывает усилие только в этой части.

4) Нагрузка приложенная к основной части конструкции дополнительно усилий не вызывает

5)Геометрические характеристики сечения, а также хар-ки упругих св-в в уравнения равновесия не входят и поэтому не влияют на значения внутренних усилий.

6)Температурные воздействия и смещение опор не вызывают появление внутренних усилий