
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Назначение и типы шпренгелей. Расчетная схема шпренгельной фермы. Определение усилий от неподвижной нагрузки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Назначение и типы шпренгелей: Фермы больших пролетов должны бать значительными высота фермы и длина пролета. Чтобы, следовательно размеры поперечных сечений сделать меньше в ферму вводят дополнительные стержни, чтобы образовать новые узлы. Эти стержни называют шпренгелями, а ферму содержащую их –шпренгельной. Шпренгели воспринимают местную нагрузку и передают ее в узлы снования фермы. Шпренгелем наз. сис-мадополн. стержней, введенных в каждую панель и разделяющих её на несколько частей. Различают 1- и 2х ярусные шпренгели. 1-ярусные восприним. и передают нагрузку в пределах одного пояса (верхнего или нижнего), а 2-ярусные передают нагрузку с одного пояса на другой. одноярусные двухъярусные
Расчетная схема шпренгельной фермы:
Расчетная схема допускает две трактовки: 1. Все стержни равноправны, в расчетной схеме они соеденены полными шарнирами. 2. Система образована положениям шпренгелей на основную ферму, при этом шпренгели представлены как дополнительная фермочка опирающаяся на узлы основной фермы.
В способе 2
При расчетах по второму в ферме выделяют стержни 3х типов: 1. Принадлежащие только осн. фермы, усилие в них определяется без шпренгельной фермы. 2. Стержни принадлежащие шпренгелю, усилия в них определяют, рассмотрим шпренгель отдельно. 3. Одновременно принадлежат шпренгелю и ферме. Усилия определяются по принципу суперпозиции N=No+Nш No,Nш- усилия в данном стержне принадлеж. осн. фермы и шпренгелю по отдельности
Определение усилий от неподвижной нагрузки:
Основные параметры трехшарнирной системы. Типы трехшарнирных систем. Определение опорных реакций. Трехшарнирные системы относятся к распорным системам, которые характеризуются тем, что вертикальные нагрузки вызывают горизонтальные опорные реакции — распор H (рис. 1, а,б,в). Это могут быть конструкции различного типа – рамы, арки, фермы, которые состоят из двух дисков, соединённых между собой шарниром и шарнирно присоединенные к земле.

Определение опорных реакций Рассмотрим эту задачу на примере арки, изображённой на рис.2. При этом будем делать сравнительный анализ реакций и усилий в арке и в балке одинакового пролёта и одного и того же загружения. Выразим длину распределения нагрузки q через l и а. Тогда а1=l/2-a. Вертикальную реакцию VA определим из уравнения статики отсюда Вертикальную реакцию VB определим из уравнения статики отсюда
Если подставить выражения VА и VВ проверка выполняется. Так как все реакции положительны, их направление изначально выбрано верно. При определении вертикальных реакций в балке используются те же уравнения статики. Поэтому вертикальные реакции в арке и балке одинаковы. Определим горизонтальные реакции. Если имеют место только вертикальная нагрузка, эти реакции будут равны, поэтому обозначать их будем H, полагая, что из уравнения статики Рассматривая равновесие арки целиком, мы не сможем подобрать уравнение статики для определения распора H. Поэтому сделаем сечение через шарнир С и рассмотрим равновесие, например, левой части арки (рис. 3). Сечение прове-
Для проверки правильности вычисления распора можно определить его ещё раз из равновесия правой части, используя уравнение Обратим внимание, что числитель в выражении распора есть балочные момент в сечении С. Тогда выражение для определения распора можно представить следующим образом Затяжка может устанавливаться на уровне опор, либо быть повышенной. Возможен случай комбинированной затяжки (рис. 4.4).
32.
Каждое сечение хар-ся 3мя геом. параметрами: лин. параметры zK, yKи уклон φK. Внутр. усилия арки удобно выражать через усилия в соотв. балке. Составим уравнение равновесия левой части конструкции: ∑МК=0. арка: МК + НуК + F(zK – a) – VAzK = 0; F(zK – a) – VAzK = -MKБАЛ. балка: MKБАЛ + F(zK – a) - VAzK = 0. MKБАЛ= -F(zK – a)+ VAБАЛzK. MK = MKБАЛ - НуК ∑h = 0; - QK - HsinφK - FcosφK + VAcosφK = 0. QK = (- F + VA)cosφK - HsinφK балка: ∑Y = 0. QKБАЛ = - F + VAБАЛ. QK = QKБАЛcosφK - HsinφK арка: ∑t = 0; NK - FsinφK + VAsinφK + HcosφK = 0. NK = (F – VA)sinφK - HcosφK. NK = - QKБАЛsinφK -HcosφK Выводы 1) при одинак. нагрузке изгиб.моменты и поп. силы в 3шарнирной системе всегда меньше, чем в соотв. балке (М<MБАЛ) 2) прод. силы N всегда меньше 0, т.к. в последней формуле 2е слагаемое по модулю больше, т.е. | HcosφK|>| QKБАЛsinφK|. HcosφK>0. т.е. арка работает на внецентренное сжатие. 3) эпюры M,Q,N в арке всегда криволин., т.к. полученные формулы содерж. функции sinφK, cosφK, которые вдоль пролета меняются нелинейно.
33.Уравнение рациональной оси трехшарнирной системы. Действие равномерно распределенной нагрузки, сосредоточенных сил и радиальной нагрузки.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 3424; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.011 с.) |











 Трехшарнирной аркой называется трехшарнирная система из двух криволинейных брусьев (рис. 1, а).
Трехшарнирной аркой называется трехшарнирная система из двух криволинейных брусьев (рис. 1, а).
























 .
.



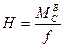 . Из этого выражения видно, что чем меньше стрела подъёма f, тем больше значение распора при одной и той же нагрузке. Таким образом, отличительной особенностью работы арки (и распорных систем в целом) является то, что в них может возникать распор большой величине (превышающий значения внешних нагрузок). Значение его тем больше, чем меньше стрела подъёма арки. Это требует установки специальных опорных устройств, препятствующих «расползанию» арки по горизонтали. В случае, если арка опирается на основание, которое не обладает соответствующим требованиям, то горизонтальный распор можно передавать на затяжку. Такая арка имеет три опорных связи (горизонтальная реакция опоры А равна нулю). Так как одна внешняя связь удаляется, устанавливается одна дополнительно внутренняя связь – затяжка, работающая на растяжение.
. Из этого выражения видно, что чем меньше стрела подъёма f, тем больше значение распора при одной и той же нагрузке. Таким образом, отличительной особенностью работы арки (и распорных систем в целом) является то, что в них может возникать распор большой величине (превышающий значения внешних нагрузок). Значение его тем больше, чем меньше стрела подъёма арки. Это требует установки специальных опорных устройств, препятствующих «расползанию» арки по горизонтали. В случае, если арка опирается на основание, которое не обладает соответствующим требованиям, то горизонтальный распор можно передавать на затяжку. Такая арка имеет три опорных связи (горизонтальная реакция опоры А равна нулю). Так как одна внешняя связь удаляется, устанавливается одна дополнительно внутренняя связь – затяжка, работающая на растяжение.








