
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные случаи применения формулы МораСодержание книги
Поиск на нашем сайте
42.Техника вычисления интегралов Мора. Основным недостатком формулы мора (техн. вычисл.инт.) явл. необходимость вычисл. интегралов для простых систем это несложно(сложно при большом числе участков). Однако имеются способы вычисления инт. Мора используя внутренние усилия называется способом перемножения эпюр. Они применяются к любому интегралу, однако рассм. их на примере эпюр изгибающих моментов.
1. Верещагина. EI=const участок прямолин.
Где Ω– площадь непрямолинейной фигуры. ус - ордината прямолинейной эпюры, взятая под центром тяжести непрямолинейной фигуры.
2. EI=const
Где а,b,c – ординаты эпюр
3. Частный случай сп. Симпсона.(2-х прямолин. эпюр)
4. Мюллера-Бреслоу.
d,c – крайние ординаты эпюр
Замечание: 1. Если ординаты перемножения эпюр находятся по разные стороны от оси, то их произведения отрицательны. 2. Сложные эпюры можно разбить на любое количество участков, перемножив эпюры на каждом участке любым способом, результаты сложить. 3. Если результаты, т.е. перемещение получается отрицательны, то перемещение противоположны приложенной силе.
Статически неопределимые системы и их свойства. Типы связей. Степень статической неопределимости.Особенности расчёта стат. Опр. систем. Степень статической наопределимости- показывает сколько система содержит избыточных или лишних связей, это число также определяет необходимость, кол-во уравнений совместности перемещений. Статически неопределимые системы(СНС) – системы, в которых уравнения статического равновессия недостаточно, дополнительно необходимо составить уравнение совместности перемещений (деформаций). Существуют связи абсолютно необходимые, усилия в них можно определить только из уравнения равновесия. В лишних связях усилия находятся из уравнения совместности деформаций. Различают внешнюю и внутреннюю статическую неопределимость. Если лишними являются опорные связи, то система внешне статически неопределима, а если связи самой системы, то внутренне.
nс может быть найдена: 1).как разность количества неизвестных реакций связей и количества независимых уравнений равновесия: 4 реакции, 3 уравнения равновесия, nс=4-3=1
2). Число степеней свободы с обратным знаком: nс= -W; nс= -3Д+2Ш+Co – общая; nс= 3К-Ш – для рамы Свойства статически неопределимых систем: 1).статически неопределимые системы более жесткие чем аналогичные статически определимые. При одной и той же нагрузке перемещения и деформации, а следовательно и внутренние усилия в них меньше 2).статически неопределимые системы сохраняют геометрическую неизменяемость после удаления лишних связей, а в статически определимых системах потеря хотя бы одной связи ведет к геометрической изменяемости системы, следовательно к неспособности нести нагрузку. 3).изменение температуры и осадка опор, а также неточность изготавления и сборки вызывают в статически неопределимых системах появление дополнительных усилий. В статически определимых системах указанные векторы вызывают только перемещения, силы и сосенты не вызывают 4)внутренние усилия в статически неопределимой системе зависят от жёсткости отдельных элементов, т.к. необходимо в процессе расчёта определитьперемещение.
Основная система и основные неизвестные метода сил
nс=3К-Ш К=2, Ш=1, nс=5
Приемы образования основной системы: 1)удаление опорных связей 2)рассечение элементов 3)введение шарниров в жесткие узлы и сечения конструкции (основная система должна быть геометрически неизменяема. Величины х1,х2,…,хn – основные неизвестные метода сил. Если в процессе расчета они «-», то их направления противоположны.
45 коля да
46. Канонические уравнения:
Для системы n раз кинематически неопределимой канонические уравнения имеют вид:
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1084; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.80.241 (0.007 с.) |


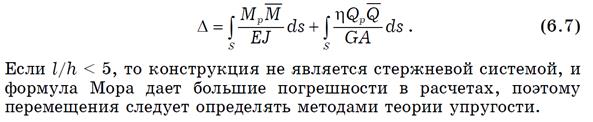




 Способы:
Способы: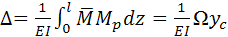 ,
, Симпсона.
Симпсона.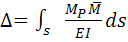 ;
;
 ;
; 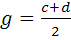 ;
; 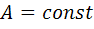 ;
; 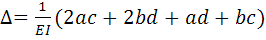

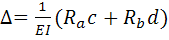 ;
;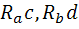 – реакции услов. Балки от фиктивной нагрузки измен. По такому же закону что и эпюра МР.
– реакции услов. Балки от фиктивной нагрузки измен. По такому же закону что и эпюра МР. .
.



 Основная система метода сил – статически определимая система полученная удалением лишних связей и заменой их реакций.
Основная система метода сил – статически определимая система полученная удалением лишних связей и заменой их реакций.





