
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет и задачи строительной механикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предмет и задачи строительной механики Строительной механикой в широком смысле следует называть науку, которая занимается разработкой принципов и методов расчета сооружений на прочность, устойчивость и жесткость. Цель расчета проектируемых новых сооружений на прочность и устойчивость состоит в том, чтобы обеспечить достаточную, но не излишнюю безопасность этих сооружений и таким образом сочетать их долговечность с экономичностью. Цель расчета на жесткость состоит в устранении возможности появления значительных деформаций сооружения (прогибов, осадок и вибраций), хотя бы и безопасных для самого сооружения, но неприемлемых с эксплуатационной точки зрения. Расчетом приходится пользоваться не только при проектировании новых сооружений, но и во всех тех случаях, когда существующее сооружение должно подвергнуться действию новых, не предусмотренных ранее нагрузок. Расчет должен выяснить, в какой степени эти нагрузки допустимы, требуется ли произвести усиление сооружения и какое именно. Значение строительной механики в современной строительной науке очень велико. Никакое сколько-нибудь ответственное сооружение не может быть спроектировано надежно и экономично без помощи расчета. Чем сложнее и крупнее сооружение, тем большее значение для сохранения жизни людей и для сбережения средств и материалов имеет расчет, производимый методами строительной механики. Расчет как бы обнажает перед взором проектировщика все статические и динамические силы, передающиеся элементам сооружения, и позволяет подобрать такие размеры этих элементов, при которых напряжения в материале будут иметь продиктованные проектировщиком величины. В СССР, где жилищное, промышленное и транспортное строительство приняло невиданные в мире размеры и где в безопасности и экономичности сооружений заинтересовано все население, строительная механика выполняет важную и почетную задачу. Было бы опасным заблуждением смотреть на строительную механику как на чисто математическую дисциплину. Поскольку она имеет дело с прочностью и жесткостью реальных сооружений, сделанных из тех или иных строительных материалов, ее выводы должны быть основаны на изучении и познании действительных свойств этих материалов, т. е. насоответствующим образом поставленных экспериментах. Тем же путем должны проверяться все допущения, касающиеся самих конструкций, все предположительные свойства, которыми мы наделяем их при выработке соответствующих методов расчета. Та же наука в течение долгого времени называлась, а некоторыми авторами и до сих пор называется «статикой сооружений» или «графической статикой сооружений». Последнее название совершенно не отвечает действительному содержанию этой науки, так как аналитические методы играют в ней не менее важную роль, чем графические. Устарелым является также название «статика сооружений», так как, помимо статики, в современной теории сооружений видное место отводится вопросам динамики.
Связи и их характеристики Каждая связь имеет две характеристики: статическая характеристика показывает, какие реакции возникают при удалении этой связи; а кинематическая характеристика показывает, каким перемещениям эта связь препятствует, а какие допускает. 1.2.1 Шарнирно-подвижная опора (стержень)

1.2.2 Шарнирно-неподвижная опора или шарнир

Шарниры, соединяющие два элемента называются простыми, а более двух – сложными или кратными.

Кратность сложного шарнира определяется по формуле: Ш=n-1, где n – число соединяемых элементов.
Кратный шарнир в расчетной схеме можно представить как несколько простых шарниров.

Жесткую заделку можно представить в виде 3-х не параллельных стержней.
Жесткое соединение можно представить в виде шарнира и стержня

1.2.4 Скользящая заделка

Эта заделка эквивалентна двум стержням
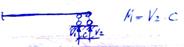

Δ- перемещение вдоль упругоподатливого стержня
φ- взаимный угол поворота элемента
Коляда
Определение опорных реакций Рассмотрим эту задачу на примере арки, изображённой на рис.2. При этом будем делать сравнительный анализ реакций и усилий в арке и в балке одинакового пролёта и одного и того же загружения. Выразим длину распределения нагрузки q через l и а. Тогда а1=l/2-a. Вертикальную реакцию VA определим из уравнения статики отсюда Вертикальную реакцию VB определим из уравнения статики отсюда
Если подставить выражения VА и VВ проверка выполняется. Так как все реакции положительны, их направление изначально выбрано верно. При определении вертикальных реакций в балке используются те же уравнения статики. Поэтому вертикальные реакции в арке и балке одинаковы. Определим горизонтальные реакции. Если имеют место только вертикальная нагрузка, эти реакции будут равны, поэтому обозначать их будем H, полагая, что из уравнения статики Рассматривая равновесие арки целиком, мы не сможем подобрать уравнение статики для определения распора H. Поэтому сделаем сечение через шарнир С и рассмотрим равновесие, например, левой части арки (рис. 3). Сечение прове-
Для проверки правильности вычисления распора можно определить его ещё раз из равновесия правой части, используя уравнение Обратим внимание, что числитель в выражении распора есть балочные момент в сечении С. Тогда выражение для определения распора можно представить следующим образом Затяжка может устанавливаться на уровне опор, либо быть повышенной. Возможен случай комбинированной затяжки (рис. 4.4).
32.
Каждое сечение хар-ся 3мя геом. параметрами: лин. параметры zK, yKи уклон φK. Внутр. усилия арки удобно выражать через усилия в соотв. балке. Составим уравнение равновесия левой части конструкции: ∑МК=0. арка: МК + НуК + F(zK – a) – VAzK = 0; F(zK – a) – VAzK = -MKБАЛ. балка: MKБАЛ + F(zK – a) - VAzK = 0. MKБАЛ= -F(zK – a)+ VAБАЛzK. MK = MKБАЛ - НуК ∑h = 0; - QK - HsinφK - FcosφK + VAcosφK = 0. QK = (- F + VA)cosφK - HsinφK балка: ∑Y = 0. QKБАЛ = - F + VAБАЛ. QK = QKБАЛcosφK - HsinφK арка: ∑t = 0; NK - FsinφK + VAsinφK + HcosφK = 0. NK = (F – VA)sinφK - HcosφK. NK = - QKБАЛsinφK -HcosφK Выводы 1) при одинак. нагрузке изгиб.моменты и поп. силы в 3шарнирной системе всегда меньше, чем в соотв. балке (М<MБАЛ) 2) прод. силы N всегда меньше 0, т.к. в последней формуле 2е слагаемое по модулю больше, т.е. | HcosφK|>| QKБАЛsinφK|. HcosφK>0. т.е. арка работает на внецентренное сжатие. 3) эпюры M,Q,N в арке всегда криволин., т.к. полученные формулы содерж. функции sinφK, cosφK, которые вдоль пролета меняются нелинейно.
33.Уравнение рациональной оси трехшарнирной системы. Действие равномерно распределенной нагрузки, сосредоточенных сил и радиальной нагрузки.
Формула Мора Если на систему действует внешн. Нагрузка, то Удлинение эл-та ds по аналогии с удлинением стержня длиной l опр-ся Δs=Np ds/EA (Δl= N l/EA) Обозначим Тогда взаимный сдвиг сечений Δy= Угол сдвига определим из закона Гука
Это в том случае,если они распеределены равномерно,однако мы рассмотрим общий случай Поэтому введем поправку в формулу: η -коэф.,учитывающий неравномерность распределения касат. Напряжений по сечению. Δy= η зависит только от формы сечения
1/ После поворота сечений,ось эл-та ds изгибается по дуге окружности Тогда ds= Δ= - Формула Мора EA, GA, EI –жесткость попер. сечений при раст. сжат. сдвиге. изгибе Np, Qp, Mp – внутр усилия, вызванные заданной внешне нагрузкой N, Q, M – внутр усилия от единичной силы, приложенные в направлении искомого перемещения. Порядок вычисления перемещения по формуле Мора: 1. Найти внутр усилия в сис-ме от нагрузки Np, Qp, Mp 2. По направлению искомого перемещения приложить ед усилия(для линейных перемещений-силу,для угловых-момент) и найти внутр усилия N, Q, M 3. Выч-ть интегралы Мора. Для сложной системы интегралы вычисляются на отдельных участках и результаты складываются.
Предмет и задачи строительной механики Строительной механикой в широком смысле следует называть науку, которая занимается разработкой принципов и методов расчета сооружений на прочность, устойчивость и жесткость. Цель расчета проектируемых новых сооружений на прочность и устойчивость состоит в том, чтобы обеспечить достаточную, но не излишнюю безопасность этих сооружений и таким образом сочетать их долговечность с экономичностью. Цель расчета на жесткость состоит в устранении возможности появления значительных деформаций сооружения (прогибов, осадок и вибраций), хотя бы и безопасных для самого сооружения, но неприемлемых с эксплуатационной точки зрения. Расчетом приходится пользоваться не только при проектировании новых сооружений, но и во всех тех случаях, когда существующее сооружение должно подвергнуться действию новых, не предусмотренных ранее нагрузок. Расчет должен выяснить, в какой степени эти нагрузки допустимы, требуется ли произвести усиление сооружения и какое именно. Значение строительной механики в современной строительной науке очень велико. Никакое сколько-нибудь ответственное сооружение не может быть спроектировано надежно и экономично без помощи расчета. Чем сложнее и крупнее сооружение, тем большее значение для сохранения жизни людей и для сбережения средств и материалов имеет расчет, производимый методами строительной механики. Расчет как бы обнажает перед взором проектировщика все статические и динамические силы, передающиеся элементам сооружения, и позволяет подобрать такие размеры этих элементов, при которых напряжения в материале будут иметь продиктованные проектировщиком величины. В СССР, где жилищное, промышленное и транспортное строительство приняло невиданные в мире размеры и где в безопасности и экономичности сооружений заинтересовано все население, строительная механика выполняет важную и почетную задачу. Было бы опасным заблуждением смотреть на строительную механику как на чисто математическую дисциплину. Поскольку она имеет дело с прочностью и жесткостью реальных сооружений, сделанных из тех или иных строительных материалов, ее выводы должны быть основаны на изучении и познании действительных свойств этих материалов, т. е. насоответствующим образом поставленных экспериментах. Тем же путем должны проверяться все допущения, касающиеся самих конструкций, все предположительные свойства, которыми мы наделяем их при выработке соответствующих методов расчета. Та же наука в течение долгого времени называлась, а некоторыми авторами и до сих пор называется «статикой сооружений» или «графической статикой сооружений». Последнее название совершенно не отвечает действительному содержанию этой науки, так как аналитические методы играют в ней не менее важную роль, чем графические. Устарелым является также название «статика сооружений», так как, помимо статики, в современной теории сооружений видное место отводится вопросам динамики.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 650; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.209.207 (0.01 с.) |













 .
.



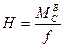 . Из этого выражения видно, что чем меньше стрела подъёма f, тем больше значение распора при одной и той же нагрузке. Таким образом, отличительной особенностью работы арки (и распорных систем в целом) является то, что в них может возникать распор большой величине (превышающий значения внешних нагрузок). Значение его тем больше, чем меньше стрела подъёма арки. Это требует установки специальных опорных устройств, препятствующих «расползанию» арки по горизонтали. В случае, если арка опирается на основание, которое не обладает соответствующим требованиям, то горизонтальный распор можно передавать на затяжку. Такая арка имеет три опорных связи (горизонтальная реакция опоры А равна нулю). Так как одна внешняя связь удаляется, устанавливается одна дополнительно внутренняя связь – затяжка, работающая на растяжение.
. Из этого выражения видно, что чем меньше стрела подъёма f, тем больше значение распора при одной и той же нагрузке. Таким образом, отличительной особенностью работы арки (и распорных систем в целом) является то, что в них может возникать распор большой величине (превышающий значения внешних нагрузок). Значение его тем больше, чем меньше стрела подъёма арки. Это требует установки специальных опорных устройств, препятствующих «расползанию» арки по горизонтали. В случае, если арка опирается на основание, которое не обладает соответствующим требованиям, то горизонтальный распор можно передавать на затяжку. Такая арка имеет три опорных связи (горизонтальная реакция опоры А равна нулю). Так как одна внешняя связь удаляется, устанавливается одна дополнительно внутренняя связь – затяжка, работающая на растяжение.





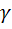 - угол сдвига
- угол сдвига ds
ds =G
=G 
 (при чистом сдвиге)
(при чистом сдвиге) Qp/A
Qp/A ds=
ds=  ds/G=ηQpds/GA
ds/G=ηQpds/GA -радиус кривизны изогнутой оси
-радиус кривизны изогнутой оси =Mp/EI
=Mp/EI , следовательно
, следовательно  =ds/
=ds/  =Mpds/EI
=Mpds/EI



